gH4zNnoHVd

УДК 621.365(075) ББК З 292.3-5я7

Л 77

Лопух Д. Б., Мартынов А. П., Вавилов А. В.

Л77 Расчет и проектирование индукционной печи с холодным тиглем: электрон. учеб. пособие, 2-е изд. доп. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2014. 31 с.

ISBN 978-5-7629-1719-3

Содержит основные сведения для расчёта индукционных печей с холодным тиглем.

Предназначено для бакалавров по профилю подготовки 140411.62 – «Электротехнологические установки и системы», а также может быть полезно инженерно-техническим работникам в этой области знаний.

УДК 621.365(075) ББК З 292.3-5я7

Рецензенты: зав. каф. электротехники и электроэнергетики, д-р техн. наук., проф. В. Я. Фролов (СПбГПУ); канд. техн. наук, доц. В. С. Федорова (ПГУПС).

Утверждено редакционно-издательским советом университета

в качестве электронного учебного пособия

2

3

1 Физические основы индукционной плавки в холодном тигле Индукционная плавка в холодном тигле (ИПХТ) получила широкое

распространение при плавке оксидов, стекол и выращивании монокристаллов благодаря ряду достоинств, которыми не обладают другие известные способы плавки этих материалов. Это, в первую очередь, чистота выпускаемого продукта: данный метод, представляющий собой совмещение незагрязняющего индукционного нагрева и незагрязняющего способа плавки, позволяет достичь необходимой степени чистоты переплавляемого материала. Кроме того, целесообразность использования ИПХТ особенно высока при переработке особо чистых и дорогих оксидов, поскольку при этом затраты на электроэнергию составляют доли процента от стоимости сырья [1].

Индукционный нагрев основан на способности электромагнитного поля проникать в толщу материала и затухать в нем, отдавая свою энергию. Если электромагнитное поле будет переменным по величине или направлению, то под действием магнитной составляющей поля в материале будет индуктироваться электродвижущая сила (ЭДС), мгновенное значение которой (в вольтах) равно [1]:

e2 = − dФ2 , dτ

где Ф2 – магнитный поток в материале.

Если зависимость магнитного потока от времени подчиняется синусо-

идальному закону Ф2 = Ф2m sin 2π f τ , то действующее значение ЭДС в мате-

риале (в вольтах) равно:

E2 = 4, 44 fФ2m ,

где Ф2m – амплитуда магнитного потока в материале; f – частота изменения поля.

В электропроводных материалах индуктированная ЭДС вызывает протекание тока:

где z2 – полное электрическое сопротивление на пути тока в материале; r2 – активное сопротивление контура тока в материале; х2 – реактивное сопротивление контура тока в материале.

4

Индуктированный ток I2 выделяет тепловую энергию на активном сопротивлении r2, которое характеризует контур тока в материале. Количество тепла в джоулях, выделяющееся за время τ, подчиняется закону ДжоуляЛенца:

Q = I22r2τ .

Тепловая мощность в ваттах, выделяющаяся в материале при протекании тока, согласно закону Джоуля-Ленца, будет равна:

Для цилиндра диаметром d2 и высотой а2, помещенного в однородное переменное магнитное поле напряженностью Н, выделяющаяся мощность будет зависеть от частоты f и свойств материала цилиндра следующим обра-

где ρ2 – удельное электрическое сопротивление материала цилиндра; А –

функция, график которой представлен на рисунке 1.1. Эта функция характеризует зависимость мощности от соотношения:

Соотношение (2) носит название относительного диаметра цилиндра и, в свою очередь характеризует степень прозрачности цилиндра для электромагнитного поля. Чем меньше m2, тем прозрачнее цилиндр.

Величина 2 есть глубина проникновения тока в материал цилиндра:

Представление о глубине проникновения тока в материал можно составить из рассмотрения неравномерного распределения плотности переменного тока j по глубине проводника в виде полубесконечной плоской стенки.

5

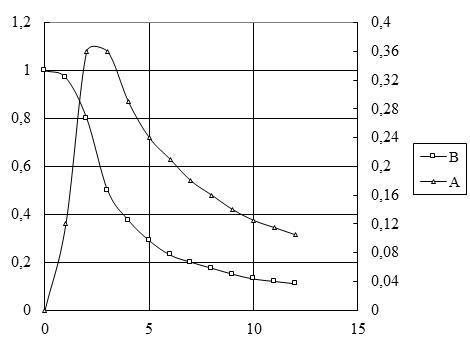
Рисунок 1.1 – Расчетные функции активного А и реактивного В сопротивления цилиндра, нагреваемого в цилиндрическом индукторе

Это явление называется поверхностным эффектом, а математическое описание его имеет вид [1]:

где z – расстояние от поверхности стенки до точки, в которой определяют плотность тока; j0 – плотность тока на поверхности стенки. Если принять z =

2, то из (3) видно, что 2 есть такая глубина, на которой плотность тока в 2,72 раза меньше, чем плотность тока на поверхности проводника.

Характерной особенностью слоя материала толщиной 2 является то,

что в нем выделяется 86,5% энергии, которую несет электромагнитная волна. При нагреве не плоских, а цилиндрических тел конечных размеров, для которых т2 > 6, глубина проникновения мало зависит от радиуса, а поверх-

ностный эффект ярко выражен. При нагреве цилиндрических тел с т2 < 3,5

распределение плотности тока в материале перестает зависеть от частоты и меняется по радиусу почти линейно. В этих случаях, по аналогии с понятием глубины проникновения, вводят понятие глубины активного слоя, характерной особенностью которого является выделение 86,5% энергии, поступающей в цилиндр.

6

Из выражения (1) и графика функции А (рисунок 1) следует, что с увеличением частоты и с возрастанием т2 индукционный нагрев становится наиболее эффективным при т2 ³ 2,5, т.е. когда D2 ³ 3,5D2. Учитывая выражение (2), можно определить минимальную частоту в герцах, необходимую для нагрева цилиндра:

f ³ 3,0 ×106 ρ2 .

D22

В расчете индукционных установок с холодными тиглями следует учитывать этот факт при подборе оптимальной частоты [2].

Вторым механизмом, обеспечивающим перемешивание расплава в тигле, является то, что в процессе плавки наружные слои расплава на глубине проникновения тока перегреваются, а глубинные остаются относительно холодными, и за счет температурного расширения осуществляется движение расплава. Скорость этого движения зависит от коэффициента линейного расширения и вязкости расплава.

2 Расчет и проектирование индукционной печи с холодным тиглем Установка для ИПХТ включает в себя: холодный тигель; цилиндриче-

ский индуктор, охватывающий холодный тигель; глухое дно. Технологически процесс плавки представляет собой садочный процесс в холодном тигле с глухим дном. Питание установки производится от высокочастотного генератора.

2.1 Тепловой расчет печи Тепловой расчет необходим для определения мощности источника пи-

тания, которая должна быть больше определенных в расчете суммарных тепловых потерь от всех поверхностей ванны расплава плюс электрические потери в элементах индукционной системы.

Принятые при расчете допущения:

1.Часть площади поверхности ванны расплава покрыта шихтой.

2.Толщина бокового и донного гарнисажей b2 постоянна по высоте и окружности ванны.

3.По толщине гарнисажа принята постоянная теплопроводность.

4.Форма ванны расплава принята цилиндрической с глубиной a2, равной диаметру d2.

7

5.Тепловой поток в боковом гарнисаже принимаем параллельным без учета кривизны его поверхности ввиду малой его толщины.

6.Температуру на границе расплав-гарнисаж принимаем равной температуре плавления.

На рисунке 2.1 показана схема баланса мощности, подводимой к индуктору и суммарных потерь мощности, где Pк – мощность тепловых потерь конвективными потоками над расплавом, кВт; Pизл – мощность излучения с поверхности расплава, кВт; Pш – мощность, передаваемая от расплава к шихте, кВт; Pбок – мощность тепловых потерь через боковую поверхность ванны, кВт; Pдно – мощность тепловых потерь через дно ванны, кВт.

Рисунок 2.1 – Схема баланса мощностей

При ИПХТ энергия, выделяемая в расплаве, расходуется на плавление шихты и поддержание ее в перегретом состоянии. Баланс тепловой мощности ванны может быть записан следующим уравнением:

где P2 – мощность, выделяемая в расплаве.

8

Тепловой процесс становится квазистационарным, если количество теплоты, выделяющееся в этом процессе превышает потери в окружающую среду. Следовательно, ИПХТ можно считать квазистационарным процессом при выполнении неравенства

мощность потерь, кВт.

Мощность потерь на излучение с зеркала ванны определяется температурой и площадью:

где С0 = 5,76 10-3 кВт/(м2 К4) – излучательная способность абсолютно черного

где Sш – площадь зеркала, засыпанного шихтой в процессе плавки, м2.

Будем считать, что во время процесса плавки шихтой засыпана половина общей площади зеркала ванны расплава, то есть Sш = 0,5S2.

Конвективные потери также пропорциональны площади поверхности зеркала, однако абсолютное их значение не велико. С достаточной точностью можно считать:

толщина гарнисажа.

9

Удельный поток тепловой мощности определяется по формуле для теплопередачи через плоскую стенку:

дачи от расплава к гарнисажу; λг – коэффициент теплопроводности гарниса-

жа; λэф – эффективный коэффициент теплопроводности прослойки газа меж-

ду гарнисажем и стенкой тигля; хз – толщина зазора; λТ – коэффициент теп-

лопроводности медной стенки тигля, равный 0,384 кВт/(м·К); хТ – толщина стенки тигля; αв – коэффициент теплоотдачи от стенки тигля к воде.

Будем считать температуру внутренней поверхности гарнисажа равной температуре плавления материала. Следовательно, тепловое сопротивление между расплавом и внутренней поверхностью гарнисажа отсутствует. Примем величину зазора между гарнисажем и стенкой тигля равной 0 (хз = 0). С высокой степенью точности можно считать, что температура на внешней стенке тигля равной температуре воды, охлаждающей тигель, то есть градиент температур по стенке тигля равен 0 из-за высокой теплопроводности медной стенки тигля. Поэтому уравнение (7) можно переписать в упрощенном виде и тепловой поток в стенку тигля будет определяться как:

λг

где Тп – температура плавления гарнисажа; Тгр – температура на границе между внешней поверхностью гарнисажа и внешней поверхностью медной стенки трубки тигля со стороны гарнисажа, которую можно найти, записав уравнение баланса тепловых потоков, поступающих из расплава в гарнисаж и из гарнисажа в стенку тигля:

λг

10