FE34kIHFh8

УДК 621.382

Моделирование биполярного транзистора при проектировании электронных схем: Электрон. метод. указ. к выполнению курсовой работы по дисциплине "Твердотельная электроника", 2-е изд. перераб. / Сост.: Б. В. Иванов, А. Д. Тупицын. СПб.: Изд-во СПбГЭТУ "ЛЭТИ", 2014. 32 с.

Курсовая работа по дисциплине "Твердотельная электроника" посвящена экспериментальному исследованию параметров биполярного транзистора для настройки его моделей, проектированию усилителя низкой частоты, использующего этот транзистор, и экспериментальному исследованию этого усилителя. Целью работы является изучение и исследование основных параметров биполярного транзистора, определяющих работу линейного усилителя низкой частоты, на основе математических моделей и экспериментальных измерений.

Методические указания предназначены студентам, обучающимся по направлению 210100.62 "Электроника и наноэлектроника".

Утверждено редакционно-издательским советом университета

в качестве электронных методических указаний

© СПбГЭТУ "ЛЭТИ", 2014

2

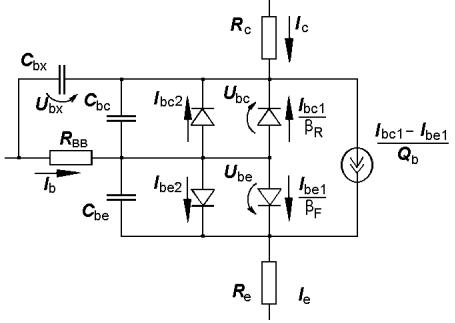
1. МОДЕЛИРОВАНИЕ БИПОЛЯРНОГО ТРАНЗИСТОРА

1.1. Модель Гуммеля – Пуна биполярного транзистора

Для расчета электронных схем, использующих биполярные транзисторы (БТ), важно выбрать модель транзистора достаточно адекватную и простую. В широком спектре моделей БТ следует выделить модель Гуммеля – Пуна, относящуюся к нелинейным схемным моделям (рис. 1.1), которая позволяет учесть эффекты, возникающие при больших смещениях на переходах [1]–[4]. Главным достоинством этой модели является то, что она в большинстве случаев позволяет получить физически интерпретируемый результат.

Рис. 1.1. Модель Гуммеля – Пуна n–p–n -транзистора

Статический режим работы транзистора описывается следующими

соотношениями:

Заряд основных носителей в базе при нулевом смещении

3

= Q1[1+ (1+ 4Q2)NK ] / 2 , Q1 = 1/(1- Ubc /UAF - Ube / UAR ),

Q2 = Ibe1 / IKF + Ibc1 / IKR .

Объемное сопротивление базы RВВ характеризуется двумя состав-

ляющими. Первая составляющая RB определяет сопротивление вывода базы и сопротивление внешней области базы, которое не зависит от тока базы Ib. Вторая составляющая RBM характеризует сопротивление активной области базы, находящейся непосредственно под эмиттером; это сопро-

тивление зависит от тока Ib. Объемное сопротивление базы RBB опреде-

ляется следующими выражениями в зависимости от параметра IRB:

Динамические свойства переходов учтены включением в модель ем-

костей коллектора, эмиттера и подложки, которые имеют диффузионные и

при Ube >FC·Uje.

Емкость перехода база – коллектор расщепляется на две составля-

ющие:

1) емкость между внутренней базой и коллектором Cbe:

4

2) емкость между внешним выводом базы и коллектором Cbx:

U bc> FC × U jc. Модель Гуммеля – Пуна включает многие физические эф-

фекты и позволяет рассчитывать характеристики электрических цепей с

биполярными транзисторами в качестве активных элементов при доста-

точно умеренных вычислительных затратах.

1.1.1. Измерение основных параметров транзистора для модели Гуммеля – Пуна

Компьютерные программы схемотехнического моделирования использующие SPICE-технологию, как правило, имеют библиотеки полупроводниковых приборов, содержащие параметры их моделей. Для биполярных транзисторов – это параметры модели Гуммеля – Пуна, поставляемые фирмами, производящими транзисторы.

Рис. 1.2. Стенд для исследования параметров усилителя на биполярном транзисторе

Однако не все существующие БТ представлены в этих библиотеках. Кроме того, из-за разброса параметры реального БТ отличаются от пара-

5

метров базового. В этом случае необходимо экспериментально измерить параметры БТ для модели Гуммеля – Пуна. Далее рассматриваются методы измерения параметров выпускаемого отечественной промышленностью транзистора П306. Измерения проводятся с помощью измерительной установки на основе универсального лабораторного стенда 87Л01 "Луч" (рис. 1.2), содержащего коммутационную плату, ряд измерительных приборов, генераторы напряжения ГН и тока ГТ.

При необходимости в качестве источников напряжения Ube и Uce ис-

пользовались стабилизированные блоки питания Б5-46 и Б5-50, а в качестве измерителей токов PA и напряжений PV универсальные электронные вольтметры В7-27. Для измерения малых токов использовался универсальный вольтметр-электрометр В7-30.

Ток насыщения IS. Для определения тока насыщения транзистора IS

необходимо получить зависимость lnIC от Ube = Ubс. Схема для измере-

ния указанных характеристик приведена на рис. 1.3. Здесь PI – измери-

тель тока коллектора (В7-30), PV1 и PV2 – измерители напряжения Ube и

Uce соответственно (В7-27). В качестве источников напряжений Ube и Uce

использовались стабилизированные блоки питания Б5-46, позволяющие регулировать выходное напряжение с шагом 10 мВ. Зависимость lnIC от

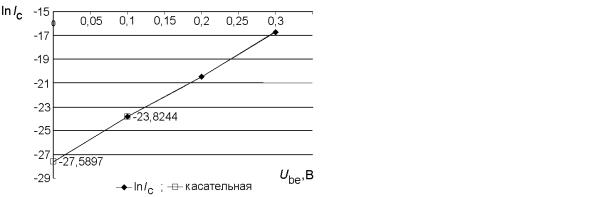
Ube = Ubс приведена на рис. 1.4.

Зависимость тока коллектора от напряжения представляет собой экс-

поненциальную зависимость и, соответственно, линейную зависимость в логарифмических координатах. Поэтому ток насыщения транзистора определяется по точке пересечения касательной с вертикальной осью ко-

ординат: IS = exp(–27,59)=1,04 пА.

6

Коэффициенты передачи по току βF и βR определяются как отноше-

ние тока коллектора к току базы в прямом активном режиме и отношение

ратор тока из состава лабораторного стенда; PV1 и PV2 – измерители

напряжений Ube и Uce соответственно; PI1 и PI2 – измерители токов базы

Ib и коллектора IС соответственно.

Для получения выходных характеристик в активном инверсном режи-

ме работы транзистора использовалась та же схема, только выводы кол-

лектора и эмиттера менялись местами.

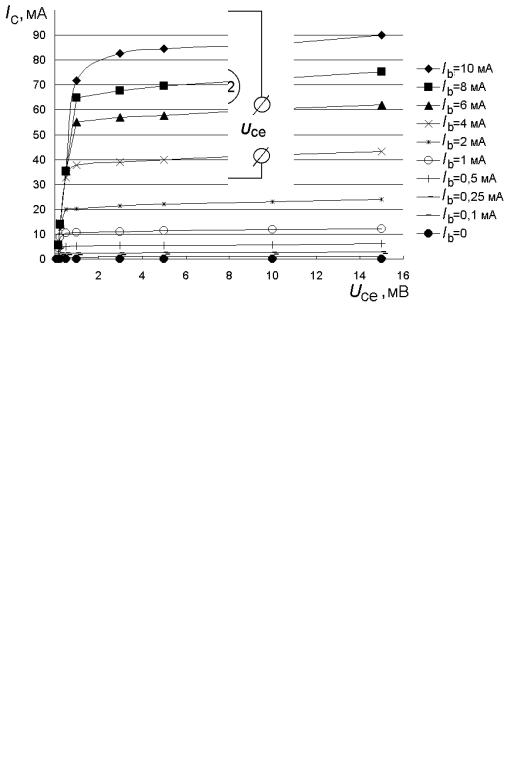
Рис. 1.6. Выходные характеристики транзистора

в нормальном активном режиме

7

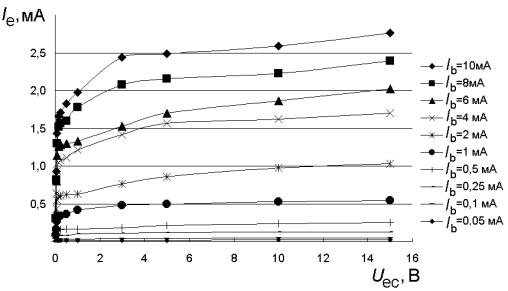
Результаты измерений в нормальном активном режиме приведены на рис. 1.6, для инверсного активного режима – на рис. 1.7. График зависи-

мости для βF строится из рис. 1.6 для заданного напряжения коллектора

Uce =10 В, соответствующего выбранной рабочей области работы бипо-

лярного транзистора. Для βR график строится аналогично из рис. 1.7 при

Uec =10 В. Выбираются максимальные значения βF и βR. Таким образом,

βF =11,8 и βR =0,527.

Рис. 1.7. Выходные характеристики транзистора

в инверсном активном режиме

Коэффициенты неидеальности переходов в нормальном и инверсном режимах NF и NR. Для нормального режима коэффициент неидеальности

NF определяет отличие наклона зависимости lnIC ≈ lnIbe1=f(Ube) от величи-

ны 1/UT. Следовательно, он может быть определён с помощью рис. 1.4 из соотношения ·∆lnIC /∆Ube = NF /UT. Отсюда коэффициент неидеальности

NF =·∆Ube/ (UT∆lnIC). В данном случае NF =0,927. Чтобы получить анало-

гичные зависимости для инверсного режима, т. е. lnIe=f(Ubc), поменяем местами коллекторный и эмиттерный выводы. Используем для определе-

ния NR выражение, аналогичное выражению для определения NF:

NR= ∆Ubc / (UT∆lnIe) =0,966.

Напряжение Эрли (UA) в нормальном активном режиме работы тран-

8

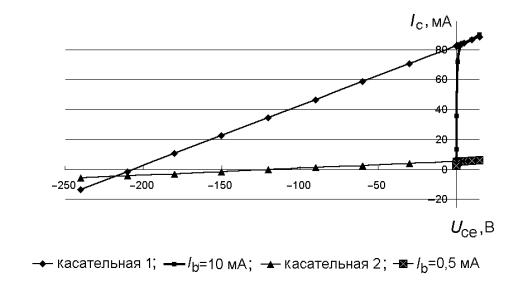
зистора определяется построением касательных к ветвям выходных ха-

рактеристик в области их насыщения. График, иллюстрирующий опреде-

ление напряжения Эрли, приведён на рис. 1.8. Здесь показаны только две из пятнадцати ветвей выходных характеристик, чтобы не загружать гра-

фик (для Ib=10 мА и Ib=0,5 мА), и касательные к ним, построенные по наклону выходных характеристик в области Uce = 5…10 B. Пересечение касательных происходит при напряжении примерно –218 В. Следователь-

но, напряжение Эрли в нормальном активном режиме составляет

UAF = 218 В. Такое его значение говорит о том, что эффект модуляции ширины базы выражен очень слабо и возможная погрешность в опреде-

лении напряжения Эрли не окажет существенного влияния на точность моделирования.

Рис. 1.8. Определение напряжения Эрли по выходным характеристикам

Аналогично может быть получено напряжение Эрли в инверсном ре-

жиме работы. Оно составляет UAR =150 В.

Токи начала спада зависимости β (IKF, IKR). В компьютерных програм-

мах, использующих модель Гуммеля – Пуна, зависимость β от тока кол-

лектора (или эмиттера) представляется в виде трёх отрезков прямых, мо-

делирующих зависимость β в областях малых, средних и больших токов.

9

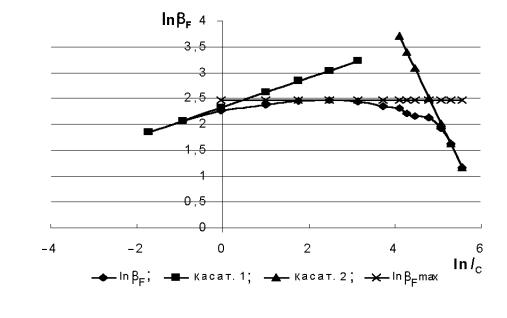
Для корректной работы программы необходимо задать значение β в обла-

сти средних токов (определены ранее) и точку перехода от горизонталь-

ного отрезка зависимости для средних токов к наклонному для больших.

Данные токи, обозначаемые IKF (forward beta roll–off corner current) или IKR

(reverse beta roll–off corner current), могут быть определены из зависимо-

стей lnβF от lnIC или lnβR от lnIe соответственно. Эта зависимость, полу-

ченная из графика для βF, приведена на рис. 1.9. Находим точки пересе-

чения касательной 2 с прямой βF=const и определяем IKF = exp(5,05)=156

мА, IKR= exp(0,2)=1,22 мА.

Рис. 1.9. Определение тока IKF перехода в режим больших токов

Коэффициенты неидеальности эмиттерного и коллекторного переходов

(NE и NC). Здесь NE – это base–emitter leakage emission coefficient и NC – base– collector leakage emission coefficient , соответственно. Определяется NE по наклону зависимости lnβF от lnIC в области малых токов. Данная зависимость приведена на рис. 1.9. Здесь NE определяется с помощью касательной 1. То-

гда можно определить значение NE из соотношения ∆lnβF/∆lnIC=1–1/NE. Отсюда

NE=∆lnIC /(∆lnIC–lnβF)=1,40. NC определим аналогично из зависимости lnβR от lnIe. В этом случае NC =∆lnIe/ (∆lnIe – – ∆lnβR)= 1,29.

10