LS-Sb89572

3.1. Основные положения

Активная газовая смесь He–Ne- лазера состоит из рабочего излучающего газа неона и буферного газа гелия. Возбуждение активной среды (АС) происходит по четырехуровневой схеме в плазме положительного столба (ПС) разряда. При столкновениях электронов ПС с атомами эффективно заселяются метастабильные уровни гелия He + e– (W1) = He* + e– (W2 < W1). Энергии воз-

буждения метастабильного уровня гелия W(He*) и возбужденного состояния неона W(Ne*), выполняющего функции верхнего лазерного уровня, близки. Благодаря этому при неупругих столкновениях реализуются условия для резонансной передачи энергии атомам неона от возбужденных частиц гелия

He* + Ne = He + Ne*. Максимальная эффективность такого обменного процесса достигается при оптимальном соотношении парциальных давлений га-

зов p(He) : p(Ne) = (5 : 1)...(15 : 1).

В дальнейшем возбужденный атом неона формирует квант индуциро-

ванного излучения: Ne* = Ne + hν. Из трех возможных каналов генерации чаще используется самый слабый, но удобный для практики видимый переход с λ = 633 нм. Для обеспечения генерации лазера требуется создание инверсии населенностей, когда концентрация возбужденных атомов на верхнем лазерном уровне (n2) становится больше, чем на нижнем (n1): ∆n = n2 – n 1 > 0.

Поддержание инверсии населенностей в АС достигается за счет эффективного заселения верхнего уровня и быстрого опустошения нижнего. Девозбуждение нижних лазерных уровней всех трех возможных излучательных переходов происходит через общее метастабильное состояние неона, расселяемое преимущественно при столкновениях Ne со стенками разрядного капилляра. В результате имеет место обратно пропорциональная зависимость усиления АС от диаметра (d) разрядного канала. Обычно d не превышает 1...3 мм, а объемы АС He–Ne- лазеров оказываются весьма незначительными.

Эффективное возбуждение высоко расположенного верхнего лазерного уровня с энергией порядка 20 эВ возможно только при достаточно высоких энергиях электронов (We), которые реализуются в ПС высоковольтного тлеющего разряда с низкой плотностью разрядного тока (I). Вероятность возбуждения атомов, а значит и n2, пропорциональна произведению концентраций возбуждаемых

атомов nа и возбуждающих электронов nе: n2 ~ nа · nе. Величину nа определяет давление газовой смеси (р), а nе – разрядный ток. Для He–Ne- лазеров существует оптимальное значение произведения суммарного давления на диаметр разрядно-

21

го канала (рd)opt = 0.44...0.53 Па · м, которому соответствует электронная темпе-

ратура Te = 105 К, оптимальная с точки зрения выхода генерации Р ~ n2 – n 1. При фиксированных значениях d и I уменьшение р снижает nа и, соответственно, n2.

Обратно пропорциональный изменению р рост Te увеличивает вероятность ионизации газа и сокращает долю энергии электронов, расходуемой на возбуждение. В итоге выходная мощность лазера Р ~ n2 – n 1 падает. Рост р сверх опти-

мального значения снижает Te, уменьшая эффективность возбуждения верхнего лазерного уровня. Одновременно увеличиваются потери We в объеме газа, воз-

растает роль “ тушащих” соударений возбужденных атомов, что также уменьшает Р. При прочих равных условиях оптимальное суммарное давление газовой смеси зависит и от разрядного тока. Чем больше ток, тем при меньших давлениях выполняются оптимальные условия генерации.

Генерация в любом лазере возникает, если усиление в АС компенсирует все виды потерь: паразитные и “ полезные”. Паразитные потери возникают из-за поглощения и рассеяния квантов на оптических элементах, “ полезные” обусловлены выходом рабочего пучка из оптического резонатора (ОР). Энергетическая характеристика He–Ne- лазера – зависимость мощности генерации от тока разряда P = f(I) носит нелинейный характер. В газоразрядном лазере величина I определяет в первом приближении концентрацию электронов – первичных возбуждающих частиц. Рост I сопровождается увеличением ne и соответствую-

щим повышением n2. При достижении порогового значения тока (Iпор) насе-

ленности верхнего и нижнего лазерных уровней выравниваются: n2 = n1. При

I > Iпор возрастание тока на начальном участке зависимости P = f(I) сопровож-

дается повышением уровня генерации лазера. Дальнейшее увеличение I приводит к активизации процесса прямого электронного заселения нижнего лазерного уровня неона – росту n1. Одновременно с ростом I повышается температура газа, усиливается тепловое заселение нижнего уровня и стимулируется рост спонтанного излучения с верхнего лазерного уровня. В результате уменьшается ∆n, и при определенном предельном токе происходит срыв генерации. Как итог, зависимость P = f(I) имеет вид кривой с максимумом при оптимальном токе.

Энергия кванта излучения с λ = 633 нм составляет всего 5 % от энергии

W(Ne*), затрачиваемой на возбуждение атома. Итог – низкий КПД АС. При типичных для He–Ne- лазеров значениях Te максимум распределения элек-

тронов по энергиям приходится на область We = kTe = 8…9 эВ и зона воз-

буждения АС с энергиями на уровне 20…21 эВ оказывается в “ хвосте” рас-

22

пределения. В результате электронный КПД – доля энергии электронов, затрачиваемая на возбуждение верхнего лазерного уровня, не превышает единиц процентов. Слабое усиление АС даже при относительно невысоком уровне потерь лимитирует допустимое пропускание рабочих зеркал значениями 2–3 %, что заметно уменьшает КПД оптического резонатора.

Рассмотренные физические особенности He–Ne- лазеров ограничивают предельную мощность излучения уровнем около 100 мВт при КПД порядка сотых долей процента.

Важнейшей характеристикой лазерного пучка является его расходимость. Теоретический минимальный угол расходимости определяется дифракцией на торце АС с поперечным размером d: Θmin ~ d/L. На практике расходимость лазерного излучения определяется многими факторами: радиусами кривизны зеркал и длиной ОР, диаметром активной среды, структурой генерируемых мод. Типичные значения угла расходимости Θ для He–Ne- лазеров составляют от долей до единиц миллирадиан. Определить угол расходимости лазерного пучка можно по изменению диаметра пучка ∆D = D2 – D1 в

двух сечениях, удаленных друг от друга на расстояние ∆L:

Классические He–Ne- лазеры выполняются в виде узких протяженных разрядных трубок, торцы которых снабжены выходными окнами. Для уменьшения паразитного отражения выходные окна располагаются под углом Брюстера. Излучение лазеров, имеющих окна Брюстера, линейно поляризовано. Современные He–Ne- лазеры с протяженностью АС до 1 м часто имеют коаксиальную конструкцию, когда цилиндрический катод расположен соосно с разрядным капилляром, а зеркала ОР являются торцевыми частями наружной стеклянной оболочки, выполняющей одновременно функции несущей конструкции ОР. Катод изготавливается обычно из алюминия, стойкого к ионной бомбардировке в плазме He–Ne- разряда.

3.2. Описание экспериментальной установки

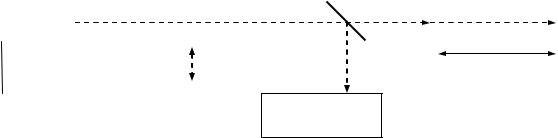
Установка построена на базе серийного He–Ne- лазера с регулируемым блоком питания (рис. 3.1). Протяженность активной среды лазера L = 0.8 м. Разрядный ток контролируется по встроенному миллиамперметру. Мощность излучения лазера (P) регистрируется фотоприемным устройством с чувствительностью 10 мкА/мВт. Контроль временных зависимостей мощности излучения осуществляется с помощью компьютерного регистратора, самопишущим прибором или вручную по цифровому прибору.

23

Рис. 3.1. Структурная схема установки

Для обеспечения возможности визуального наблюдения и регистрации картин распределения интенсивности в поперечном сечении лазерного пучка,

измерения его диаметра и расходимости на пути луча помещаются разнесен-

ные в пространстве экраны. Для контроля вида поляризации лазерного излу-

чения используется вращаемый анализатор на основе поляроидной пленки,

снабженный шкалой отсчета углов поворота. Изучение свойств светоделите-

лей лазерного излучения производится с помощью прозрачной стеклянной пластины, поворот которой возможен вокруг ортогональных осей x, y, лежа-

щих в плоскости, перпендикулярной лазерному лучу.

3.3.Порядок выполнения работы

1.Включить измерительные приборы.

2.Переключатель диапазонов тока на лицевой панели установить в по-

ложение 4, ручку потенциометра плавной регулировки тока – в крайнее пра-

вое положение, соответствующее максимальному разрядному току. С разре-

шения преподавателя включить сетевой тумблер, дождаться возбуждения разряда в лазере и с помощью потенциометра установить ток I = 30 мА.

3. В течение 15…20 мин зарегистрировать поведение мощности излуче-

ния лазера Р = f(t) в ходе установления теплового режима.

4. Зарегистрировать установившееся значение мощности излучения ла-

зера P0. Установить анализатор (поляроид) на пути лазерного пучка перед светоделителем. Исследовать зависимость мощности пропускания анализа-

тора от угла его поворота Pτ = f(Θ) с угловым шагом 30° в пределах полного оборота. Убрать анализатор.

5. Установить прозрачную стеклянную пластину на пути лазерного пуч-

ка перед светоделителем. Поочередно исследовать зависимости мощности,

пропускаемой пластиной, от угла ее поворота Pτ = f(Θ) вокруг ортогональных осей x и y. Угол Θ изменять с интервалом 5° в пределах 0...85°.

24

6. Исследовать энергетическую характеристику лазера – зависимость выходной мощности от тока P = f(I) в диапазоне Imin… Imax, обеспечиваемом блоком питания.

7. В том же диапазоне токов с помощью двух экранов, разнесенных на расстояние ∆L = 6.5 м, исследовать зависимости диаметров лазерного пучка от тока: D1 = f(I) и D2 = f(I). Одновременно для каждого из 4–5 значений тока зарегистрировать картины распределения интенсивности в поперечном сечении лазерного пучка по дальнему экрану.

8. При токе, близком к оптимальному значению, исследовать зависимости диаметров лазерного пучка от уровня мощности генерации лазера: D1 = f(Р) и

D2 = f(Р). Одновременно для каждого из 4–5 значений мощности генерации зарегистрировать картины распределения интенсивности в поперечном сечении лазерного пучка по дальнему экрану.

3.4.Содержание отчета

1.Цель и содержание работы.

2.Схема экспериментальной установки.

3.Таблицы и графики зависимостей P = f(t), P = f(I), D2 = f(I), Θ = f(I) и

соответствующие им картины распределения интенсивности излучения в поперечном сечении лазерного пучка.

4.Таблицы и совмещенные графики зависимостей P = f(I), D2 = f(I), Θ = f(I)

исоответствующие им картины распределения интенсивности излучения в поперечном сечении лазерного пучка.

5.Таблицы и совмещенные графики зависимостей D2 = f(P ), Θ = f(Р) и

соответствующие им картины распределения интенсивности излучения в поперечном сечении лазерного пучка.

6. Зависимости коэффициента пропускания анализатора от угла поворо-

та τан = Pτ/P0 = f(Θ). По характеру зависимости определить вид поляризации лазерного излучения.

7. Зависимости коэффициентов отражения пластины от угла ее поворота ρпл = f (Θ) вокруг ортогональных осей x и y. Поглощением пластины прене-

бречь и полагать, что ρпл = 1 – τпл.

8. Зависимость КПД лазера η = P/Pнак = f(I). Мощность накачки лазера определяется как Pнак = UI. Падение напряжения на трубке определяется по вольт-амперной характеристике лазера U = f(I) (табл. 3.1).

25

Таблица 3.1

9. Расчетные зависимости продольного градиента потенциала в положи-

тельном столбе разряда Ez = f(I). При расчетах продольного градиента пола-

гать Ez = 0.8U(I)/LАС.

10. Рассчитать и построить зависимость порогового показателя усиления

зеркал ОР (α1, α2 – потери на зеркалах; τ1, τ2 – коэффициенты пропускания зеркал). При расчете полагать α1 = α2 = 2 % и τ1 = 0.2 %, τ2 = 2 %, диапазон изменения L = 0.4…1.2 м.

11. Выводы по работе и протокол испытаний.

4. МОДЕЛИРОВАНИЕ ПРОЦЕССА ВОЗНИКНОВЕНИЯ ПОПЕРЕЧНЫХ МОД ЛАЗЕРА

Цель работы – ознакомление с причинами возникновения и типами по-

перечных мод лазера, методами их моделирования и селекции.

4.1. Основные положения

При генерации лазера в его оптическом резонаторе (ОР) протяженно-

стью L устанавливаются определенные собственные типы колебаний – моды,

образующихся в результате взаимодействия встречных потоков индуциро-

ванных квантов. Кванты, распространяющиеся строго вдоль продольной оси z, формируют так называемые продольные (аксиальные или осевые) моды,

характеризуемые индексом q. Индекс продольных мод q = L/(λ/2) – целое число полуволн λ, укладывающихся на длине ОР вдоль оси z. Число N одно-

временно генерирующих продольных мод зависит от превышения усиления над уровнем потерь в ОР для конкретной моды. В первом приближении N

определяется отношением ширины зоны генерации к величине межмодового интервала ОР, равного c/(2L). При N = 1 режим работы лазера называют од-

ночастотным, при N > 1 режим становится многочастотным.

26

Внеосевое излучение, распространяющееся в ОР под небольшими углами φi, образует поперечные (внеосевые или угловые) моды. Те колебания, для ко-

торых фазовые граничные условия образования стоячих волн не выполняются,

подавляются резонатором. Каждой частоте колебаний и каждому возможному направлению распространения φi, удовлетворяющим условиям генерации, со-

ответствуют определенные распределения фаз, напряженности электрического поля Е и плотности мощности I в продольном и в поперечных направлениях.

Все возможные моды ОР в целом относятся к классу поперечных электро-

магнитных колебаний – ТЕМmnq. В оптическом диапазоне, где L >> λ, индекс q

имеет порядок 105...106, поэтому его опускают и тип волны (поперечную моду)

обозначают как ТЕМmn. Индексы поперечных мод m и п определяют число из-

менений знака Е на поверхности зеркала, соответственно, по координатам x и y.

Для основной поперечной моды низшего порядка (т = п = 0), распро-

страняющейся строго вдоль оптической оси z резонатора, поверхность зерка-

ла является поверхностью равной фазы. Распределение интенсивности в по-

перечном сечении пучка моды ТЕМ00 является равномерным, близким к гауссовому. Поперечные моды более высоких порядков (m + n > 0) распро-

страняются под небольшими углами φi к оси z ОР. В результате поверхность зеркала перестает быть поверхностью равной фазы электрического поля оп-

тической волны, а распределение интенсивности в поперечном сечении пуч-

ка становится неравномерным – пятнистым. В силу малости возможных зна-

чений углов φi индексы п и т имеют значение порядка единиц, в редких слу-

чаях превышают уровень более десяти. Поперечные моды не только нару-

шают однородность пучка, но и увеличивают его расходимость.

В зависимости от формы зеркал, геометрии активного элемента и рас-

пределения инверсии населенностей (усиления) в объеме могут возникать поперечные моды с прямоугольной или с осевой симметрией. Для случая наиболее распространенной прямоугольной симметрии индексы т и п могут быть определены на практике как число максимумов интенсивности (пятен) в

плоскости зеркала без единицы, соответственно, по координатам x и y. Для мод с осевой симметрией (цилиндрических мод) индексы т и п – число вари-

аций знака Е в плоскости зеркала, соответственно, по радиусу и по азимуту.

Основной тип цилиндрической моды ТЕМ00 в поперечном сечении имеет кольцевое распределение интенсивности.

27

Кванты, распространяющиеся строго вдоль ОР, имеют наименьшие по-

тери, многократно взаимодействуют с активной средой и испытывают мак-

симальное усиление. В лазере возможна одновременная генерация несколь-

ких типов конкурирующих поперечных мод. Высокодобротные моды низких порядков сосредотачиваются в приосевой зоне максимального усиления и вытесняют низкодобротные моды к периферии пучка. На состав генерируе-

мых лазером поперечных мод влияют и случайные технические факторы:

наличие пыли и дефектов на оптических элементах, неоднородность АС и т.

п., что нарушает классические распределения и может непредсказуемо усложнить картину интенсивности излучения в поперечном сечении пучка.

4.2.Программа расчета распределений электрического поля

иинтенсивности излучения в конфокальном резонаторе

Расчет поля и интенсивности собственных колебаний в ОР с произвольной конфигурацией зеркал затруднителен. Частным случаем ОР является симметричный конфокальный резонатор, состоящий из двух одинаковых сферических зеркал, фокусные точки которых совмещены: L = R1 = R2 = 2F.

Точку F принимают за начало системы координат x, y, z, полагая ось z осью ОР. В лазерах L многократно превышает длину волны и поперечный размер пучка на зеркале: L >> λ и L >> 2а, а число Френеля NФ > 1. Для таких усло-

вий поперечное распределение электрического поля Еmnq(x, y) собственных колебаний ТЕМmnq ОР в плоскости xy в первом приближении описывается произведениями полиномов Эрмита Н(m, x), Н(n, y) и функции Гаусса

где Н(m, x), Н(n, y) – полиномы Эрмита, степень которых определяется индексами m для координаты х и n – для у; re = f(z) – увеличивающийся с ро-

стом z радиус пучка, соответствующий спаду интенсивности в е раз.

Для низших степеней полиномы Эрмита имеют вид Н0(х) = 1; Н1(х) = 2х;

Н2(х) = 4х2 – 2; Н3(х) = 8х3 – 12 х; Н4(х) = 16х4 – 48 х2 + 12. Интенсивность излучения пропорциональна квадрату напряженности электрического поля Imnq(x, y) ~ [Еmnq(x, y)]2. Для основной поперечной моды ТЕМ00 полиномы принимают единичные значения, и распределение интенсивности в попереч-

28

ном сечении пучка будет гауссовым. Гауссов пучок является расходящимся. Более 90 % энергии пучка локализовано в телесном угле Θ = λ/L.

Используя теорию конфокального резонатора и средства Mathcad 14, можно получить наглядное представление о распределениях электрического поля и интенсивности излучения по координатам, в поперечном сечении пучка и в трехмерном пространстве. В среде Mathcad 14 полиномы Эрмита задаются встроенными функциями H(n1, x) и H(n2, y), где n1, n2 – индексы m

и n соответственно; r = re. Все расчеты электрического поля и интенсивности излучения проводятся в относительных единицах. Для удобства расчетов полагается r = 1 и Е = 1. Диапазон изменения координат х и у –4…4 с шагом 0.01. Для расчета напряженности поля используется выражение

Плотность мощности излучения рассчитывается как

I0 (x, y, n1, n2 ) := (E0 (x, y, n1, n2 ))2 .

Варьируемыми параметрами являются индексы ТЕМ-моды n1 и n2.

4.3.Порядок выполнения работы

1.Включить компьютер.

2.Выбрать папку “Ma ткад ТЕМ” и открыть файл “ Моды”.

3.Задать значения индексов поперечной моды: n1 = 0 и n2 = 0.

4.Зарегистрировать распределения электрического поля Е0 и интенсив-

ности излучения I0 по координатам х, у, в поперечном сечении пучка – плос-

кости ху и в трехмерном пространстве хуz.

5. Повторить пп. 3, 4 для нескольких комбинаций индексов n1, n2, по за-

данию преподавателя.

4.4.Содержание отчета

1.Цель и содержание работы.

2.Схема экспериментальной установки.

3.Графики и картины распределений электрического поля Е0 и интен-

сивности излучения I0 по координатам х, у, в поперечном сечении пучка – плоскости ху и в трехмерном пространстве хуz для пп. 3–5.

4. Выводы по работе.

29

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Пихтин А. Н. Оптическая и квантовая электроника. М.: Высш. шк., 2001. Смирнов Е. А. Светотехнические электронные приборы и устройства:

Учеб. пособие. СПб.: Изд-во СПбГЭТУ “ ЛЭТИ”, 2010.

Смирнов Е. А., Черниговский В. В. Автоматизированный расчет и проектирование приборов квантовой электроники: Учеб. пособие. СПб.: Издво СПбГЭТУ “ ЛЭТИ”, 2005.

Смирнов Е. А., Черниговский В. В. Применение лазеров: Учеб. пособие. СПб.: Изд-во СПбГЭТУ “ ЛЭТИ”, 2001.

Смирнов Е. А., Черниговский В. В. Расчет и проектирование приборов квантовой электроники: Учеб. пособие / ЛЭТИ. Л., 1988.

Смирнов Е. А., Черниговский В. В. Физические основы лазеров и их типы: Учеб. пособие. СПб.: Изд-во СПбГЭТУ “ ЛЭТИ”, 2005.

Характеристики элементов квантовой электроники: Методические указания / Сост. Е. А. Смирнов. СПб.: Изд-во СПбГЭТУ “ ЛЭТИ”, 2006.

30