5856

11

например, так: 0 – не приедет; 1 – приедет в понедельник; …; 7 – приедет в воскресенье. Отсюда вывод: чем больше m, тем больше информации (сведений) можно вложить в данный символ. Но использование символов с боль-

шим m порождает ряд проблем (см., например, разд. 2.), поэтому часто для передачи сообщения используют не один, а несколько m-ичных символов.

Кодовая комбинация Χ [1] , Χ [2] ,..., Χ [n] , состоящая из m-ичных символов, нередко называется кодовым словом длины n. Другое возможное название - это n-разрядное m-ичное число. Пусть все n символов, входящих в это слово, имеют один и тот же алфавит x1 , x2 ,..., xm .

Пока рассматриваем эту комбинацию как единое целое и перечислим все её возможные состояния:

Отсюда следует, что комбинация символов, в принципе, ничем не от-

личается от одного М-ичного символа, если не считать использования громоздких обозначений для каждой из М букв алфавита (1.3). И в этом случае для полного описания сигнала нужно знать ряд распределения (1.1), который в первой строке содержит возможные значения сигнала (1.3), а во второй строке – числа, т.е. вероятности появления каждого из этих значений

причем сумма этих М вероятностей, естественно, равна единице.

Далее, формула (1.2) определяет способ вычисления любой числовой характеристики и для кодовой комбинации, и в этом случае она принимает вид

ятностные и числовые характеристики для любого символа или группы символов, входящих в комбинацию.

Для примера рассмотрим комбинацию Χ,Υ , состоящую из двух (n=2) m-ичных символов. Имея m2 вероятностей совместного появления значений x j и yk (1.5), по формуле сложения вероятностей можно найти вероятности

для каждого из символов

Далее, воспользовавшись формулой умножения вероятностей

p xj , y p x j p y / x j p y p x j / y , (1.8)

можно построить m условных рядов распределения символа X, по одному ря-

13

Полное описание непрерывной случайной величины содержит её плотность вероятностей W x . Это неотрицательная функция, удовлетворяющая условию нормировки

Любую из числовых характеристик находим с помощью формулы, подобной (1.2),

задав функцию x соответствующего вида. Одной из самых полезных мо-

делей является нормальная (гауссовская) случайная величина, для которой кривая плотности вероятностей – колокольного вида

где mx и x – математическое ожидание и среднеквадратическое отклонение

соответственно.

Полной характеристикой последовательности непрерывных случай-

ных величин Χ [1] , Χ [2] ,..., Χ [n] является совместная плотность вероятностей

W x[1] , x[2] ,..., x[n] .

Для определения числовых характеристик используется аналог форму-

лы (1.6)

Чтобы использовать более компактные обозначения, систему случай-

а вектор её конкретных значений точно так же обозначить строчной буквой

х.

Наиболее часто используются следующие числовые характеристики: вектор-строка математических ожиданий

и, следовательно, ковариационная матрица R является диагональной.

14

Система n гауссовских случайных величин описывается плотностью вероятностей

где detR – определитель матрицы R, xT – вектор-столбец x .

1.4 Непрерывные сигналы

Математической моделью непрерывного (аналогового) сигнала является непрерывный случайный процесс X t . Такой процесс характеризуется

ансамблем (множеством) реализаций. Ничтожная часть этого множества для примера показана на рис. 1.1 (кстати, если бы эти 5 реализаций, изображенных на рисунке, составляли всё множество, то их с полным правом можно было бы считать сигналами, отображающими 5 возможных значений пятиричного символа).

Вид каждого элемента этого множества, в принципе, известен заранее,

X(t)

0

T t

Рис. 1.1. Часть ансамбля реализаций непрерывного случайного процесса

а вся случайность заключается в том, что заранее неизвестно, которая из этих реализаций появится.

Вероятностное описание непрерывного процесса традиционно начинается с того, что мысленно проводят его квантование по времени с шагомt Tn , где n – количество отсчетов, получающихся в результате квантования. В итоге непрерывный случайный процесс X t заменяется последова-

тельностью непрерывных случайных величин-отсчетов X [1] , X [2] ,..., X [n] . Далее для этой системы случайных величин определяют желаемые вероятностные характеристики по методике, описанной в разд. 1.3. И, наконец, предполагают, что предельные значения этих характеристик при t 0 являются характеристиками самого случайного процесса X t .

Наиболее важные числовые характеристики непрерывного случайного

15

процесса: математическое ожидание mx t –детерминированная функция ( аналог вектора (1.17)) и ковариационная функция R t1 , t2 (аналог (1.18)).

Для стационарного случайного процесса математическое ожидание – это константа mx , а ковариационная функция является детерминированной

функцией одной переменной t1 t2 .

Для стационарного случайного процесса наглядной характеристикой является спектр плотности мощности G , связанный с ковариационной функцией R парой преобразований Фурье

Понятие непрерывной случайной функции широко применяется для описания многих реальных сигналов. В частности, звуковой сигнал – это непрерывный случайный процесс X t . Изображение – это случайная функция

X y1 , y2 двух пространственных координат y1 и y2 (случайную функцию нескольких переменных называют случайным полем).

1.5 Аддитивные и мультипликативные помехи

Сигнал на выходе передатчика x t , распространяясь вдоль линии, связывающей пункты передачи и приема, изменяет свою форму. В итоге на выходе линии (на входе приемника) имеем сигнал y t , отличающийся от переданного. Проблема заключается в том, что эти изменения случайны (детерминированные изменения сигнала, возникающие в линии, в принципе, всегда могут быть точно учтены и полностью скомпенсированы, поэтому пока мы их не будем рассматривать). Такая случайная трансформация сигнала в линии называется воздействием случайной помехи.

Помеха Z t называется аддитивной (от английского add-прибавлять),

если

где k – постоянный коэффициент передачи линии.

Причиной возникновения аддитивной помехи являются существующие всегда тепловой шум, электромагнитные поля, создаваемые посторонними источниками излучения естественного и искусственного происхождения, и т.п.

В качестве модели аддитивной помехи обычно принимают белый шум,

т.е. стационарный гауссовский случайный процесс, имеющий нулевое математическое ожидание и равномерный и бесконечно широкий спектр плотно-

16

сти мощности. Если реализацию белого шума подать на вход идеально-

го полосового фильтра, обладающего единичным коэффициентом передачи в полосе частот

(1.23)

то на выходе фильтра будем иметь реализацию также стационарного гауссовского случайного процесса V t с нулевым математическим ожиданием,

называемого ограниченным по полосе белым шумом.

счетов Найквиста-Котельникова, являются независимыми случайными величинами и описываются n-мерной совместной плотностью вероятностей

W (v1,..., vn ) W (v1 ) W (vn )

Величина N0 – это спектральная плотность мощности белого шума и в соот-

ветствии с (1.24) она имеет размерность энергии Вт·с.

Мультипликативная помеха (от английского multiply-умножать) обычно является следствием многолучевости при радиосвязи в условиях, когда электрические свойства атмосферы или рельеф подстилающей поверхности случайным образом изменяются в пространстве и во времени (распространение радиоволн в городе или в неоднородной атмосфере).

Общий подход к описанию мультипликативной помехи заключается в том, что линия с многолучевостью представляется как линейный фильтр со случайно изменяющимися параметрами

где Sx – спектр сигнала x t ,

– передаточная функция этого фильтра, которая является комплексной случайной функцией двух переменных (для обычного фильтра с постоянными параметрами она зависит лишь от ).

Наиболее важные числовые характеристики статистически однородной передаточной функции – это ширина tн её временной ковариационной

функции

18

характеристику помехи первого типа можно перенести на помеху второго типа, поменяв местами переменные t и , т.е. сам сигнал и его спектр

S y . Случайные искажения спектра сигнала приводят к тому, что импульсы

в процессе передачи случайным образом искажаются, растягиваются (рассеиваются) во времени тем больше, чем больше отношение н , при этом

средняя величина рассеяния во времени имеет порядок .

Понятно, что помехоустойчивость приема сигнала, форма которого случайна, ниже по сравнению с ситуацией, когда форма ожидаемого сигнала известна заранее. Более того, рассеяние во времени приводит к наложению соседних импульсов друг на друга и к их дополнительным искажениям. Та-

кое явление известно как межымпульсная или межсимвольная интерференция.

Если t tн и н , то форма сигнала не искажается

H t0, 0 являются случайными величинами. В итоге это определяет случайность амплитуды и фазы принимаемого сигнала y t . Если же t tн ин , то существенно совместное влияние мультипликативной помехи

обоих типов.

Более того, многолучевость приводит ещё и к появлению пространственных селективных замираний, т.е. к случайным искажениям в пространстве амплитуд и фаз волн в пункте приема. В итоге флуктуации сигналов, принимаемых двумя разнесенными в пространстве антеннами, становятся всё менее зависимыми при увеличении разнесения. Для большинства каналов при разнесении антенн на расстояние в (10…100) эти флуктуации становятся практически независимыми.

Наличие любой помехи (аддитивной или мультипликативной) приводит к тому, что принимаемый сигнал y t практически всегда отличается по форме от переданного сигнала x t .

1.6 Методы аналитического и геометрического представления сигналов и помех

Вероятностные модели сигналов и помех, описанные в разд. 1.1–1.5, вполне пригодны в качестве исходного материала для решения большинства задач теории электрической связи. Поэтому разработка новых моделей не является целью данного раздела. Здесь мы напомним те известные образы функций, задающих форму сигналов и помех, которые позволят в дальнейшем упростить и сделать более наглядным описание операций (не меняя их сути), которые мы будем проводить над сигналами.

19

Как было отмечено, любой сигнал (с помехой или без нее) – это функция времени U t , характеризующая изменение напряжения или тока в некоторой точке тракта передачи.

Узкополосный сигнал, у которого ширина спектра намного мень-

где функции A t 0 и t в явном виде задают законы амплитудной и фазовой модуляции соответственно. Зачастую ещё более удобна запись такого сигнала в виде суммы двух колебаний

сигнала.

И, наконец, для действительного узкополосного сигнала широко используется представление в виде “аналитического сигнала”

медленноменяющиеся функции, т.е. каждая из них относительно мало изменяется на интервале времени T 2 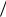0 , равном периоду несущей частоты.

Легко убедиться в этом преимуществе, если воспользоваться векторным представлением сигнала U t , т.е. отображать его в виде вектора на

плоскости в декартовой системе координат xOy так, что в любой момент времени длина вектора равна A t , а угол с осью Ox равен t . Поскольку полная фаза сигнала t растет довольно быстро, вектор будет совершать в среднем f0 оборотов в секунду. Использование понятия аналитического сиг-

нала (или квадратурных составляющих) позволяет применить то же представление к комплексной величине . В итоге скорость вращения вектора окажется значительно меньше, позволяя более детально проследить динамику развития колебаний. В этой ситуации направления двух осей координат символизируют колебания одной и той же частоты f0 , но сдвинутые по фазе на 90о.

20

Другая возможность для создания довольно наглядного образа сигнала

– это использование геометрического представления сигнала. Такая воз-

можность вытекает из естественной или искусственно созданной дискретности сигнала U t во времени и может применяться к сигналам с любой шириной спектра. Например, цифровой сигнал (последовательность символов-

ни (ввиду возможности использования такого перехода каждый элемент вектора u сразу умножили на постоянную величину

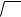
Итак, каждому сигналу соответствует своя точка (вектор) в n-мерном пространстве (не путать с описанным выше векторным представлением колебаний). Поэтому посмотрим, какие свойства сигналов отображают основные геометрические понятия.

1) Норма (длина) вектора U в евклидовом пространстве равна

j 1

Если исходный сигнал U t был непрерывным, то перейдем к пределу и получим

где Eu – энергия сигнала (по умолчанию принимается, что входное сопротивление цепи Rвх 1Ом). Возможные значения 0 U . Обратим внимание на

этот факт: длина вектора, соответствующего сигналу, зависит не от напряжения, тока или мощности, а от энергии этого сигнала. Это обстоятельство определяет для цифровых сигналов способ введения такого важного понятия, как отношение сигнал/шум.

Если сигнал (1.38) – это последовательность двоичных символов (нулей и единиц), то удобнее использовать n-мерное пространство Хэмминга. В нем длина вектора численно равна его весу S W S , т.е. определяется как

количество единиц в этом векторе. Возможные значения S 0;1; 2;...; n – это целые числа.