
1253
.pdf
61
Подставив полученные выражения для корреляционного интеграла (2.54) и энергии (2.55) в формулу (2.49) и учитывая плотность вероятности w( ) , найдём выражение для безусловного отношения правдоподобия:
l(r(t)) exp |
E |
1 |
2 |
exp |
2Z |
cos( Q) d . |
||
|
|
|
|
|
||||
N0 |
2 |
0 |
N0 |
|||||
|
|
|
||||||
Известно, что
1 |
2 |
|
|
|
||
|
|
exp(u cos( |
Q))d |
I0 (u) |
(2.56) |
|
2 |
||||||
0 |
|
|
|
|||
|
|
|
|
|
||
есть модифицированная функция Бесселя нулевого порядка. Это чётная |
||||||
функция своего аргумента, причём I0 (0) |
1 (рисунок 2.13). Учитывая фор- |
|||||
мулу (2.56), запишем отношение правдоподобия для сигнала со случайной начальной фазой в окончательном виде:
l(r(t)) exp |
E |
I0 |
2Z |
, |
(2.57) |
|
|
||||
|
N0 |
|
N0 |
|
|
где Z определяется из соотношений (2.51) и (2.52).
2.3.4 Отношение правдоподобия для сигнала со случайными начальной фазой и амплитудой
Предположим, что обнаруживаемый сигнал задан выражением (1.10), в
котором |
0 |
0. |
Пусть начальная фаза |
равномерно распределена на |
|
|
|
|
|
интервале |
|
, |
, а амплитудный коэффициент A представляет случайную |
|
величину с плотностью вероятности Рэлея при среднеквадратичном значении, равном единице.
Рисунок 2.13 |
|
|
||
Для независимых величин A и |
совместная плотность вероятности |
|||
определяется следующим образом: |
|
|||
w( , A) |
1 |
2 Aexp( A2 ), A |
0; |
|
2 |
||||
|
|
|
||
( , |
). |
|
|
|
62
Вычислим корреляционный интеграл z(r(t) | , A) и энергию E( , A)
для фиксированных значений параметров |
и A. По аналогии с п. 2.3.3. |
|
можно получить: |
|
|
z(r(t) | |
, A) AZ cos( Q) ; |
|
E( , A) |
A2 E , |
|
где выражения для Z , Q и E совпадают с аналогичными в п. 2.3.3. В отличие от рассмотренного случая сигнала со случайной начальной фазой
энергия E( |
, A) |
зависит от случайного амплитудного множителя A. Сред- |
|
нее значение энергии определяется следующим образом: |
|||
|
2 |
|
|
E |
dA |
E( , A)w( , A)d |
E 2A3 exp( A2 )dA E , |
ср |
|
|
|
0 |
0 |
|
0 |
т.е. среднее значение равно энергии сигнала при частном значении
A 1.
Используя общую формулу (2.49), получим выражение для отношения правдоподобия в виде
l(r(t)) |
|
1 |
|
dA2 |
|
A exp( A2 ) exp |
A2 E |
exp |
2 AZ |
cos( |
Q) d . |
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
N0 |
N0 |
|
||||||
Применив формулу (2.56), а также табличный интеграл |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
I |
|
( |
x) exp( |
|
x2 )xdx |
exp |
|
|
, |
|
|
(2.58) |
|||||||||
0 |
|
2 |
4 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим окончательное выражение отношения правдоподобия для сиг- |
|||||||||||||||||||||
нала со случайными начальной фазой и амплитудой: |
|
|
|
||||||||||||||||||
|
|
|
|
|
N |
0 |
1 |
|
|
Z 2 |
|
|
|
|
|
|
|
||||
l(r(t)) |
|
exp |
|
|
|
|
|
|
, |
|
|
|
|
(2.59) |
|||||||
E |
|
N0 |
N0 |
|
|
E N0 |
|
|
|
|
|||||||||||
где величина Z определяется по формулам (2.51) и (2.52).
2.3.5 Структурные схемы оптимальных обнаружителей сигналов со случайными параметрами
Алгоритмы оптимального обнаружения рассматриваемых сигналов реализуются на основании полученных выражений для отношения правдоподобия (2.57) и (2.59) и правила (2.20). Решающее правило можно преобразовать, имея в виду, что сравнение с порогом остаётся в силе для любой монотонной функции от отношения правдоподобия.
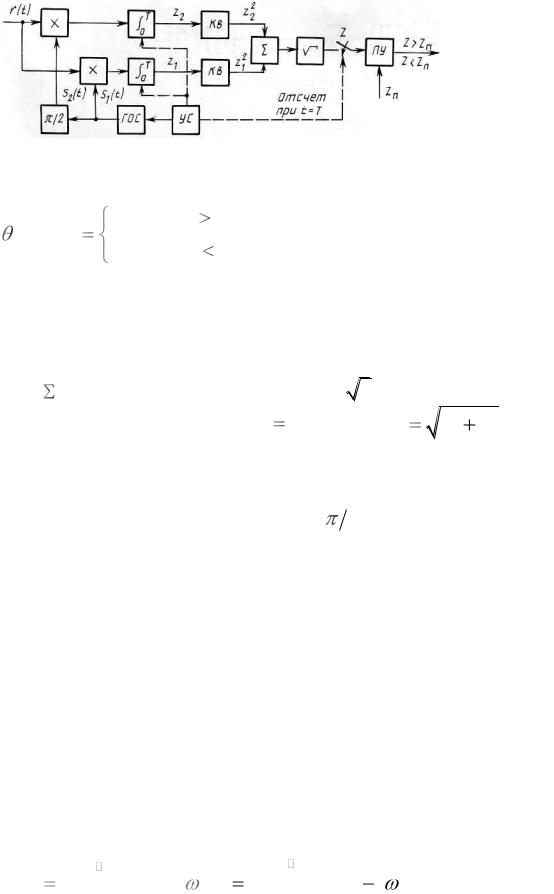
63
Рисунок 2.14 – Структурная схема квадратурного приёмника
На этом основании запишем оптимальное решающее правило:
* |
(r(t)) |
1, |
если Z |
Zп ; |
(2.60) |
opt |
|
0, |
если Z |
Zп . |
|
|
|
|
Используя выражение (2.60), а так же соотношения определяющие величину Z , структурную схему обнаружителя можно представить в виде, изображённом на рисунке 2.14. Такую схему называют квадратурным приёмником. Квадратурные каналы организуют благодаря включению фазовращателя в цепь опорного сигнала одного из перемножителей. Квадраторы (Кв),
сумматор ( ), вычислитель квадратного корня ( |
) обеспечивают формиро- |
|||
|
|
|
|
|
вание на входе ПУ в момент времени t T значения Z |
z2 |
z2 |
. Наличие |
|
|
|
1 |
2 |
|
двух каналов исключает возможность потери полезного сигнала вследствие незнания его начальной фазы. При отсутствии приращения корреляционного интеграла, например, в первом канале, второй канал обеспечивает прираще-
ние за счёт сдвига фазы опорного сигнала на |
2. Схема, представленная на |
рисунке 2.14, как и схема, изображённая на рисунке 2.1, требует знания временного положения ожидаемого сигнала. Если время запаздывания сигнала неизвестно , оптимальный обнаружитель усложняется. При разбиении интервала неопределённости времени запаздывания на элементарные участки, длительность каждого из которых определяется требуемой разрешающей способностью, можно построить многоканальный обнаружитель. Каждый канал его настраивается на сигнал с соответствующим ожидаемым запаздыванием. Решение об обнаружении сигнала принимается одновременно с оценкой времени запаздывания.
Вместо схемы с квадратурными каналами используют схему с согласованным фильтром. Возможность использования согласованных фильтров в обнаружителях сигналов, имеющих случайные параметры, основывается на следующих рассуждениях. Из соотношений (2.50) и (2.51) следует необходимость формирования квадратурных компонентов сигнала.
Представим эти компоненты в следующем виде:
s (t) |
Re(S 0 (t) exp( j |
0 |
t)) |
Re(S* (t) exp( j |
0 |
t)) ; |
1 |
|
|
0 |
|
64
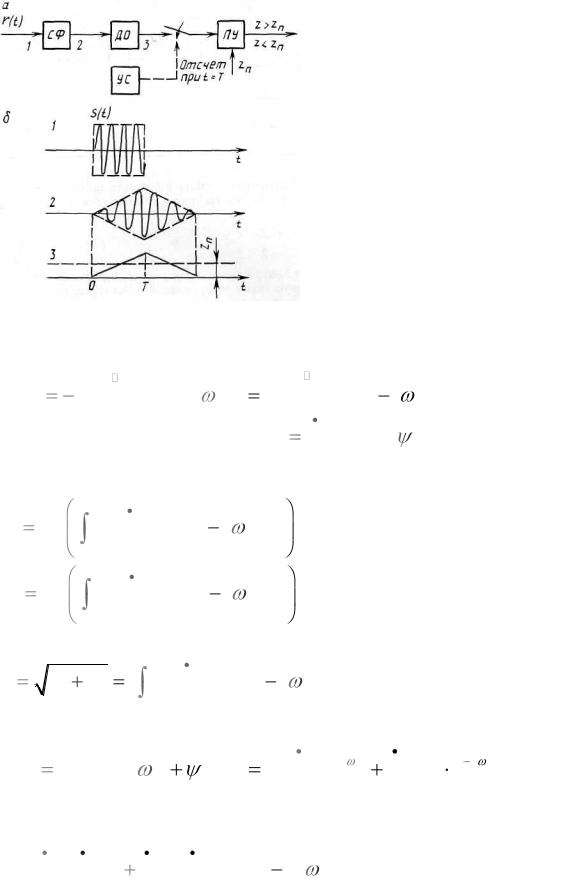
Рисунок 2.15 – Структурная схема обнаружителя сигнала со случайной фазой (или со случайными фазой и амплитудой)
s (t) |
Im(S 0 (t) exp( j |
0 |
t)) Im(S* (t) exp( j |
0 |
t)) , |
|
2 |
|
|
0 |
|
||
где комплексная огибающая S0 (t) |
S0 (t) exp( j |
(t)). Знак «*» озна- |
||||
чает комплексно-сопряжённую функцию. В соответствии с соотношениями (2.51) и приведёнными выражениями запишем:
|
T |
* |
|
|
z1 |
Re |
r(t) S 0 (t) exp( |
j |
0t)dt ; |
|
0 |
|
|
|
|
T |
* |
|
|
z2 |
Im |
r(t) S 0 (t) exp( |
j |
0t)dt . |
0
Величина z представляет модуль комплексного числа:
|
|
|
|
T |
|
* |
|
|
|
|
|
|
|
z |
z2 |
z2 |
|
r(t) S 0 (t) exp( |
|
j |
0 |
t)dt |
. |
(2.61) |
|||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
|
|
|
|
||
Используем очевидное равенство |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
* |
|
r(t) |
R(t) cos( |
0t |
R (t)) |
(R(t)e j 0t |
R (t)) e j 0t . |
||||||||
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
При этом подынтегральное выражение в формуле (2.61) представим в виде суммы:
**
0, 5(R(t) S 0 (t) R (t) S 0 (t) exp( j2 0t)),

65
в которой второе слагаемое представляет быстро осциллирующую функцию с частотой 2 0 . Интеграл от такой функции можно считать приближённо равным нулю. Поэтому
|
1 |
|
T |
* |
|
|
z |
|
|
|
R(t) S 0 (t)dt |
. |
(2.62) |
2 |
|
0 |
||||
|
|
|
|
|
Полученному выражению ставится в соответствие схема, содержащая
*
согласованный фильтр (СФ) с импульсной реакцией S 0 (t) и включенный
после СФ линейный детектор огибающей (ДО), который реализует операцию взятия модуля. Структурная схема обнаружителя сигнала со случайной фазой или со случайными фазой и амплитудой представлена на рисунке 2.15, а, временные диаграммы в точках 1-3, поясняющие работу схемы, - на рисунке
2.15, б.
2.3.6 Качественные показатели обнаружения сигналов со случайными параметрами
Для определения характеристик обнаружения сигналов со случайными параметрами необходимо знать условные плотности вероятности случайной величины Z при наличии и отсутствии сигнала в наблюдаемой смеси. Плотность вероятности можно определить из выражения для совместной
плотности вероятности w(Z,Q) , проинтегрировав её по всем возможным значениям Q . Совместная плотность вероятности w(Z,Q) вычисляется на основании совместной плотности вероятности w(z1, z2 ) путём перехода к новым переменным с учётом якобиана преобразования.
Рассмотрим обнаружитель сигнала, содержащего случайную фразу |
и |
||
случайную амплитуду A, подчиняющуюся распределению Рэлея. При из- |
|||
вестной амплитуде сигнала плотность вероятности |
w(A) |
(A 1) , |
т.е. |
принимается A 1. При отсутствии сигнала w(A) |
(A) , т.е. принимается |
||
A 0.
Можно показать по аналогии с соотношениями (2.23) и (2.24), что для любого фиксированного значения A средние значения случайных величин z1
и z2 и их дисперсии определяются выражениями:
|
|
T |
|
AE cos |
; |
|
z1,2 |
A |
s(t, )s1,2 |
(t)dt |
|||
AE sin |
; |
|||||
|
|
0 |
|
|||
|
|
|
|
|
||
|
|
T T |
|
|
|
|
2 |
2 |
n(t1 )n(t2 ) s1,2 (t1 )s1,2 |
(t2 )dt1dt2 N0 E 2 . |
|||
z |
z |
|||||
1,2 |
|
|
|
|
|
|
0 0
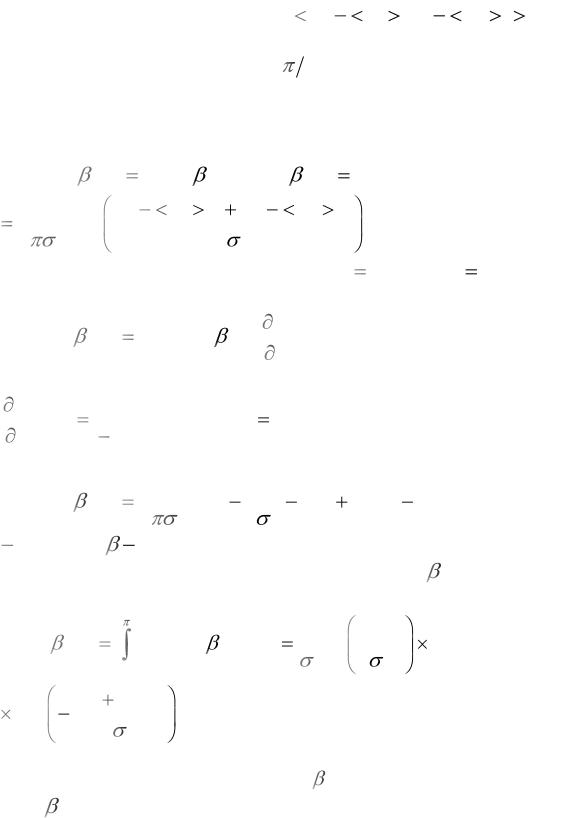
66
Случайные величины z1 и z2 некоррелированы и подчиняются гаус-
совскому закону распределения. Следовательно, эти величины статистически независимы. Некоррелированность вытекает из приближенного равенства ну-
лю смешанного центрального момента (z1 z1 z2 ) . Действительно, этот момент сводится к интегралу от произведения двух колеба-
ний s1 (t) и s2 (t) , сдвинутых по фазе на |
2, при этом интеграл практически |
||||||||||||||||||||||||||||||
равен нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Совместная условная плотность вероятности случайных величин z1 и |
|||||||||||||||||||||||||||||||
z2 с учётом их независимости определяется выражением |
|
||||||||||||||||||||||||||||||
|
w(z1, z2 | , A) |
|
w(z1 | , A)w(z2 | , A) |
|
|
|
|
|
|||||||||||||||||||||||
1 |
|
|
|
|
|
(z |
|
|
z )2 |
(z |
2 |
|
|
z |
2 |
|
|
)2 |
|
|
|
|
|||||||||
|
|
|
|
exp |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
||||||||
2 |
2 |
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Полагая на основании выражения (2.53) |
z1 |
|
Z cos Q, z2 |
Z sin Q, пе- |
|||||||||||||||||||||||||||
рейдём к новым переменным двухмерной плотности и вероятности |
|||||||||||||||||||||||||||||||
|
w(Z,Q | |
|
, A) |
|
w(z , z |
|
| |
, A) |
(z1, z2 ) |
|
, |
|
|
|
|
||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
(Z,Q) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(z1, z2 ) |
|
|
cos Q |
sin Q |
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
(Z , Q) |
|
|
Z sin Q |
Z cos Q |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
есть якобиан преобразования. После преобразования получим |
|||||||||||||||||||||||||||||||
|
w(Z,Q | |
|
, A) |
|
Z |
|
exp( |
1 |
|
|
(Z 2 |
|
A2 E2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
2 |
|
2 |
2 |
|
|
2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
||
|
2AEZ cos( |
|
|
Q))) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Одномерная условная плотность вероятности w(Z | , A) |
вычисляется |
||||||||||||||||||||||||||||||
путём интегрирования правой части полученного выражения по Q : |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
AEZ |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
w(Z | |
, A) |
|
w(Z , Q | , A)dQ |
|
|
I0 |
|
|
|
|
||||||||||||||||||||
|
|
|
2 |
2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
z |
|
|||
|
exp |
|
|
|
Z 2 |
A2 E2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Произведя усреднение по параметрам |
|
|
|
и A с учётом плотности веро- |
|||||||||||||||||||||||||||
ятности w( |
, A), найдём искомую плотность вероятности величины Z : |
||||||||||||||||||||||||||||||
|
|
|
67 |
w(Z ) |
1 |
2 |
d w(Z | , A)w( A)dA. |
|
|
||
2 |
|
||
|
0 |
0 |
|
|
|
Вид этой плотности вероятности меняется в зависимости от заданной плотности вероятности w( A), поэтому целесообразно рассмотреть частные случаи:
1) при (A 1) (сигнал со случайной начальной фазой и неизвестной амплитудой)
w |
(Z ) |
Z |
exp |
Z 2 |
E2 |
I |
|
ZE |
, Z 0 |
; |
(2.63) |
|
|
|
0 |
|
|||||||
с.п |
|
2 |
|
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
z |
|
|
z |
|
|
z |
|
|
|
Рисунок 2.16 – Кривые условных плотностей вероятности wп (Z ) и wс.п (Z) при обнаружении сигнала со случайной начальной фазой.
Рисунок 2.17 - Семейство характеристик обнаружения.
2) при w( A) |
2Aexp( A2 ) |
- рэлеевском распределении (сигнал со |
|||||||||||||
случайными амплитудой и начальной фазой) |
|
|
|||||||||||||
wс.п |
(Z ) |
|
|
2Z |
|
exp |
|
|
Z 2 |
|
|
, Z 0 |
; |
||
2 |
2 |
E2 |
|
2 |
2 |
E2 |
|||||||||
|
|
|
|
z |
|
|
|
|
|
|
z |
|
|
|
|
3) при w(A) |
|
(A) (сигнал отсутствует) |
|
||||||||||||
w (Z ) |
Z |
exp |
|
Z 2 |
, Z |
0 . |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
п |
|
2 |
|
|
2 |
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
z |
|
|
|
|
z |
|
|
|
|
|
|
|
68
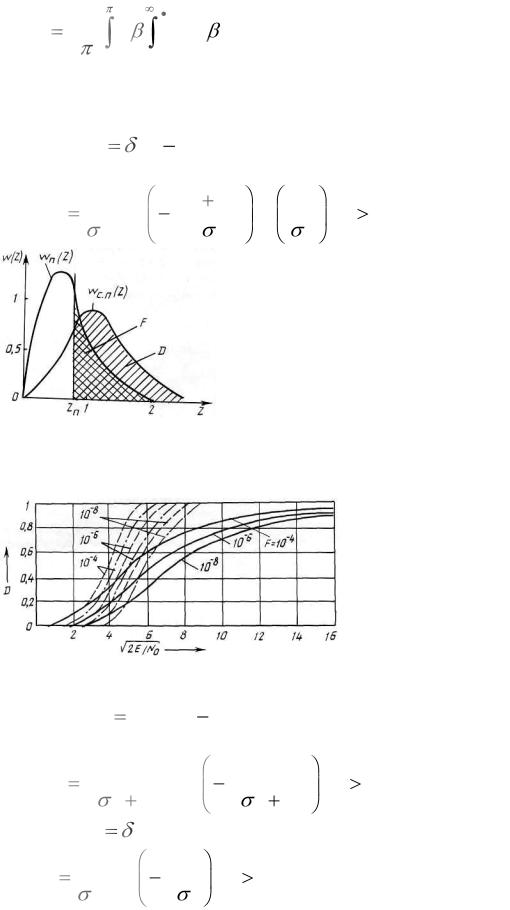
Здесь при интегрировании использована табличная формула (2.58). Кривые условных плотностей вероятности wп (Z ) и wс.п (Z) при обнаруже-
нии сигнала со случайной начальной фазой приведены на рисунке 2.16. Заштрихованные площади под кривыми справа от прямой, проходящей через
пороговое значение Zп , соответствуют вероятностям ложной тревоги F и правильного обнаружения D .
Рисунок 2.18
Введём переменную
Z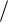 z и относительный порог hп Zп
z и относительный порог hп Zп 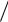 z .
z .
Тогда с учётом параметра обнаружения q |
2E N0 (отношения сигнал/шум) |
|||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
2 |
|
|
D |
I0 ( |
q ) exp |
|
|
|
d ; |
||
|
|
|
|
|||||
|
|
2 |
|
|||||
|
hп |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
exp |
2 2 d |
exp h2 |
2 . |
||||
|
|
|
|
|
|
п |
|
|
|
hп |
|
|
|
|
|
|
|
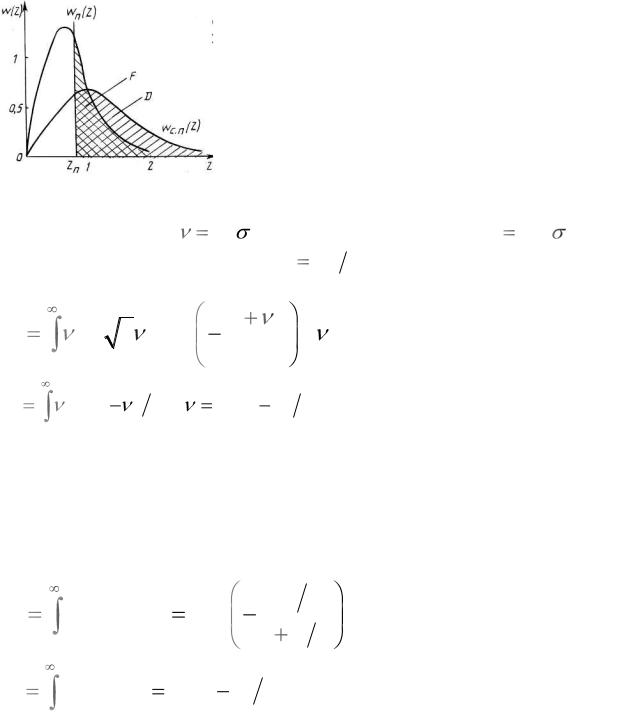
Приведённые соотношения определяют семейство характеристик обна- |
||||||||
ружения, показанных на рисунке 2.17 (штрихпунктирные кривые).
При сигнале со случайной амплитудой и начальной фазой условные вероятности D и F определяются площадями, заштрихованными под кривыми
wс.п (Z) и wп (Z ) на рисунке 2.18. Эти вероятности вычисляются по следующим формулам:
|
|
|
|
h2 |
2 |
|
|
|
D |
wс.п (Z )dZ |
exp |
|
п |
|
; |
(2.64) |
|
1 |
q 2 |
|||||||
|
hп |
|
|
|
||||
|
|
|
|
|
|
|
||
F |
wп (Z )dZ |
exp hп2 2 . |
|
|
(2.65) |
|||
|
hп |
|
|
|
|
|
|
|
69
Исключив величину hп из соотношений (2.64) и (2.65), получим
D F(1 q 2) 1
2) 1
Кривые обнаружения, соответствующие данному случаю, приведены на рисунке 2.17 (сплошные). Для сравнения на этом же рисунке показаны кривые обнаружения сигнала с полностью известными параметрами (штриховые). Из анализа кривых можно сделать вывод о том, что для обнаружения
сигнала со случайными параметрами требуется большая энергия, чем для обнаружения полностью известного сигнала при условии одинаковых качественных показателей обнаружения. Кривые обнаружения для сигнала со случайной амплитудой при больших значениях вероятности D смещаются вправо особенно сильно, что объясняется возможностью значительных замираний сигнала в канале распространения и снижением качества обнаружения. Вместе с тем при малых значениях D (менее 0,2) из-за случайного характера амплитуды возможно некоторое улучшение качества обнаружения по сравнению с сигналом, имеющим известную амплитуду и случайную начальную фазу.
2.4Обнаружение пачек импульсов
2.4.1 Отношение правдоподобия для сигналов в виде флуктуирующей и нефлуктуирующей пачек радиоимпульсов со случайными начальными фазами
Модель сигнала в виде некогерентной пачки радиоимпульсов задана выражением (1.21). Начальные фазы радиоимпульсов i i , i 1,..., k (k- число импульсов в пачке), считаем независимыми случайными величинами,
каждая из |
которых равномерно |
распределена на |
интервале |
, , т.е. |
||||||||
w |
i |
1 |
2 |
, |
i |
1,..., k . Совместная плотность вероятности совокупно- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
сти независимых случайных величин |
1,..., |
k определяется выраже- |
||||||||||
нием |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
w |
|
|
w( |
i ). |
|
|
|
|
|
(2.66) |
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
Как и в п. 2.3.3, по формуле косинуса суммы приводим выражение |
|||||||||||
(1.11) к следующему виду: |
|
|
|
|
|
|||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
s |
t, |
|
|
s1i |
t |
cos |
i |
s2i |
t sin i , |
|
(2.67) |
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
s1i |
t |
S0i t cos |
0t |
i |
t |
, |
|
|
|||
|
s2i |
t |
S0i |
t |
sin |
0t |
|
i t . |
|
|
||
70
Условное значение корреляционного интеграла можно записать на основе выражения (2.67):
|
|
|
k |
|
z r(t) | |
r(t)s(t, |
)dt |
(z1i cos i z2i sin i ) , |
(2.68) |
|
|
|
i 1 |
|
где интегралы взяты без конкретизации пределов и принято |
|
|||
z ji |
r(t)s ji (t)dt, j |
1, 2;i |
1,..., k . |
|
Обозначив

 z12i z22i Zi ,
z12i z22i Zi ,
приведём выражение (2.68) к виду
|
k |
|
z(r(t) | ) |
Zi cos( i Qi ). |
(2.69) |
i 1
Если пачка состоит из неперекрывающихся импульсов, то энергия пачки определяется суммой энергий импульсов. При малом изменении амплиту-
ды и фазы |
i (t) |
в пределах импульса за время периода колебаний высокой |
||||||||
частоты можно записать: |
|
|
|
|
|
|
||||
|
k |
|
|
k |
1 |
S 2 |
k |
|
|
|
E( |
) |
E ( |
i |
) |
|
(t)dt |
E |
, |
(2.70) |
|
|
||||||||||
|
|
i |
|
2 |
0i |
|
i |
|
|
|
|
i 1 |
|
|
i 1 |
|
i |
1 |
|
|
|
где энергия i -го импульса Ei не зависит от случайной начальной фазы i . Используя общую формулу (2.49), с учётом выражений (2.66), (2.69),
(2.70) представим отношение правдоподобия в виде
k |
|
Ei |
1 |
2 |
|
2Zi |
|
|
|
|
|
|
|
l(r(t)) |
exp |
|
exp |
cos |
|
Q |
d |
|
. |
||||
|
|
|
|
|
i |
i |
|||||||
|
|
N0 |
2 0 |
|
N0 |
i |
|
|
|||||
i 1 |
|
|
|
|
|
|
|
||||||
На основе формулы (2.56) после интегрирования из полученного выражения следует
k |
|
Ei |
|
2Zi |
|
|
|
l(r(t)) |
exp |
I0 |
. |
(2.71) |
|||
N0 |
N0 |
||||||
i 1 |
|
|
|
|
Выражение (2.71) показывает, что отношение правдоподобия пачки
неперекрывающихся импульсов со случайными независимыми начальными фазами определяется произведением отношений правдоподобия для каждого импульса пачки.
Вычислим отношение правдоподобия для сигналов в виде пачек флуктуирующих радиоимпульсов со случайными начальными фазами. Ограничимся рассмотрением случая независимых флуктуаций, когда модель сигнала
