6655

41

находит А, то В получает штраф 1 ден. ед. от А, в противном случае В платит А 1 ден. ед. Необходимо построить платежную матрицу игры.

Игрок В может искать игрока А в убежище стратегия В1, либо в убежище стратегия

В2. Если игрок А находится в убежище и там его обнаруживает игрок В, т.е. осуществляется пара стратегий (А1, В1), то игрок А платит штраф, т.е. а11 = 1.

Аналогично получаем, что а22 = 1(А2, В2). Очевидно, что стратегии (А1, В2) и (А2, В1) дают игроку А выигрыш 1, поэтому а12 = а21 = 1. Таким образом, для игры «поиск№ размера 2 2 получаем платежную матрицу:

Рассмотрим игру m n с матрицей Р = aij, i = 1, 2, …, m; j = 1, 2, …, n и определим наилучшую среди стратегий A1, A2, …, Am. Выбирая стратегию Ai, игрок А должен рассчитывать, что игрок В ответит на нее той из стратегий Bj,при которой выигрыш игрока А минимален (игрок В стремится «навредить» игроку А). Обозначим через I

наименьший выигрыш игрока А при выборе им стратегии Ai для всех возможных стратегий игрока В (наименьше

е число в i-той строке платежной матрицы), т.е. minj = 1, … n aij = i. Среди всех чисел i

(i = 1, 2, …, m) выберем наибольшее:

= maxi = 1, …m i.

Назовем нижней ценой игры, или максимальным выигрышем (максимином). Это гарантированный выигрыш игрока А при любой стратегии игрока В. Следовательно, = maxi = 1, …m minj = 1, … n aij .

Стратегия, соответствующая максимину, называется максиминной стратегией. Игрок В заинтересован в том, чтобы уменьшить выигрыш игрока А; выбирая стратегию Bj, он учитывает максимально возможный при этом выигрыш для А. Обозначим :

j = maxi = 1, …,m aij.

Среди всех чисел j выберем наименьшее = minj = 1, …, n j и назовем верхней ценой игры

или минимаксным выигрышем(минимаксом). Это гарантированный выигрыш игрока В.

Следовательно,

= minj = 1, …, n maxi = 1, …,m aij.

Стратегия, соответствующая минимаксу, называется минимаксной.

42

Принцип, диктующий игрокам выбор наиболее «осторожных» минимаксной и максиминной стратегий, называется принципом минимакса. Этот принцип следует из разумного предположения, что каждый игрок стремится достичь цели, противоположной цели противника. Определим нижнюю и верхнюю цены игры и соответствующие стратегии для игры «поиск». Рассмотрим платежную матрицу Р. При выборе стратегии А1

(первая строка матрицы) минимальный выигрыш равен:

1.1.5.1.2.1.1 1 = min ( 1,1) = 1

и соответствует стратегии 1 игрока В. При выборе стратегии А2 (вторая строка матрицы)

минимальный выигрыш равен:

1.1.5.1.2.1.2 2 = min ( 1,1) = 1,

он достигается при стратегии В2.

Гарантируя себе максимальный выигрыш при любой стратегии игрока В, т.е. нижнюю цену игры = max( 1, 2) = max( 1, 1) = 1, игрок А может выбирать любую стратегию:

А1 или А2, т.е. любая его стратегия является максиминной.

Выбирая стратегию В1 (столбец 1), игрок В понимает, что игрок А ответит стратегией А2,

чтобы максимизировать свой выигрыш (проигрыш В). Следовательно, максимальный проигрыш игрока В при выборе им стратегии В1 равен 1 = max( 1, 1) =1. Аналогично.

Максимальный проигрыш игрока В (выигрыш А) при выборе им стратегии В2 (столбец 2)

равен 2 = max( 1, 1) =1.

Таким образом, при любой стратегии игрока А гарантированный минимальный проигрыш игрока В равен = min( 1, 2) = min( 1, 1) = 1 верхней цене игры. Любая стратегия игрока В является минимаксной. Построим следующую таблицу с использованием платежной матрицы Р:

В этой задаче верхняя и нижняя цены игры различны: . Если верхняя и нижняя цены игры совпадают, то общее их значение называется чистой ценой игры, или ценой

43

игры. Минимаксные стратегии, соответствующие цене игры, называются оптимальными чистыми стратегиями, а их совокупность решением игры. Про саму игру говорят, что она решается в чистых стратегиях. В этом случае игрок А получает максимальный гарантированный выигрыш , а игрок В добивается минимального гарантированного проигрыша . Говорят, что решение игры обладает устойчивостью, т.е. если один из игроков придерживается своей оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей оптимальной стратегии.

Пара чистых стратегий (Ai, Bj) дает оптимальное решение игры тогда и только тогда, когда соответствующий ей элемент aij является одновременно наибольшим в своем столбце и наименьшим в своей строке. Такая ситуация, если она существует, называется седловой точкой.

Пример 1. Игрок А записывает одно из двух чисел: 1 или 2; игрок В одно из трех чисел:

1, 2 или 3. Если оба числа одинаковой четности, то игрок А выигрывает и выигрыш равен сумме этих чисел, если четности не совпадают, то В выигрывает, выигрыш равен сумме этих чисел. Построить платежную матрицу, определить верхнюю и нижнюю цены игры и проверить наличие седловой точки.

Решение.

1.1.5.1.3 Седловая точка отсутствует.

5.3 Геометрическая интерпретация игры 2 2.

Решение игры 2 2 допускает наглядную геометрическую интерпретацию. Пусть игра задана платежной матрицей Р = aij, i = 1, 2;j = 1, 2 . По оси абсцисс отложим единичный отрезок А1А2; Точка А1 (x=0) изображает стратегию А1, а все промежуточные точки этого отрезка смешанные стратегии SA первого игрока, причем расстояние от SA до правого конца отрезка это вероятность р1 стратегии А1, расстояние до левого конца отрезка

44

вероятность р2 стратегии А2 . На перпендикулярных осях и откладываем выигрыши при стратегиях А1 и А2 соответственно. Если второй игрок примет стратегию В1, то она даст выигрыш а11 и а21 на осях и , соответствующие стратегиям А1 и А2. Обозначим эти точки на осях и буквой В1. Средний выигрыш 1,

соответствующий смешанной стратегии SA, определяется по формуле математического ожидания 1 = а11р1 + а21р2. и равен ординате точки М1, которая лежит на отрезке В1В1 и

имеет абсциссу SA.

ТЕМА №6

ЗАДАЧИ МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ

6.1 Постановка задачи

Задачи многокритериальной оптимизации возникают в тех случаях, когда имеется несколько целей, которые не могут быть отражены одним критерием. Рассмотрим решение таких задач методом последовательных уступок.

Пусть частные критерии могут быть упорядочены в порядке убывания их важности. Предположим, что все частные критерии максимизируются и пронумерованы в порядке убывания их важности. Находим максимальное значение Z1 первого по важности критерия в области Q допустимых решений путем решения однокритериальной задачи:

Z1 X max

X Q

Затем, исходя из практических соображений и принятой точности, назначается величина допустимого отклонения 1 >0 критерия Z1 и находим максимальное значение

второго по важности критерия Z2 при условии, что значение первого критерия не должно отклоняться от своего максимума более чем на величину допустимой уступки, т.е. решается задача:

Z2 X max

Z1 X Z1 1 , X Q.

Снова назначается величина уступки 2 >0 по второму критерию, которая вместе с первой уступкой используется для нахождения условного максимума третьего частного критерия:

45

Z3 X max

Z1 X Z1 1 ,

Z2 X Z2 2 ,

X Q.

Аналогичные процедуры повторяются до тех пор, пока не будет выявлено максимальное значение последнего по важности критерия. Полученное на последнем этапе решение считается оптимальным.

6.2 Пример решения задачи многокритериальной оптимизации.

Пусть задача трехкритериальной оптимизации имеет вид:

Z1 x1 2x2 max

Z2 2x1 x2 max

Z3 x1 3x2 max

x1 x2 6, 1 x1 3, 1 x2 4,

1 3, 2 53 .

Решение:

Максимум первой функции Z1 можно найти, например, графическим методом или

Далее уступаем по критерию Z2 на величину соответствующей уступки, и решаем еще одну ЗЛП:

46

Z3 x1 3x2 max

x1 x2 6, 1 x1 3, 1 x2 4,

x1 2x2 4 ,

2x1 x2 7 .

И оптимальное решение получаем в виде: X 3 2, 3 , Z3 7 .

Таким образом, оптимальные значения частных критериев при оптимальных

2. ЗЛП не имеет решения, если:

а) система ограничений несовместна; б) линейная форма не ограничена снизу; в) область определения не ограничена; г) неравенства в ограничениях имеют разные знаки.

3. Область определения ЗЛП представляет собой:

а) неотрицательный многогранник; б) выпуклый многогранник; в) замкнутую ломаную; г) замкнутую ломаную, ограничивающую выпуклый многогранник.

4. Решение ЗЛП всегда достигается:

а) внутри области определения; б) на границе области определения; в) в вершине области определения; г) в точке, ближайшей к началу координат.

5. Найти ошибки в записи первой симплекс-таблицы:

47

6. Записать оптимальный план ЗЛП и оптимальное значение линейной формы (с указанием вида экстремума) по следующей последней симплекс-таблице:

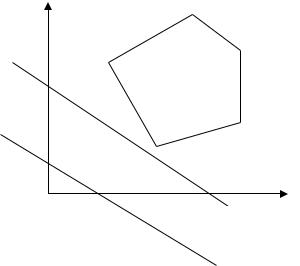
7. Отметить планы ЗЛП, изображенных на рисунках 1 и 2, доставляющие максимум и минимум линейной форме:

L(X)=-4

L(X)=-10

D

49

9. Для каждой пары симметричных взаимно двойственных задач из предыдущего пункта установить соответствие между переменными задач, исходные задачи решить графически, записать решение обеих задач.

2.Транспортная задача разрешима тогда и только тогда,

когда…………………………………………….: (записать формулу)

3.Открытые ТЗ: «на избыток», если..………………………………….; «на недостаток», если………………………………….

4.Укажите тип транспортных задач из пункта 1): закрытая - ……..; «на избыток» - …………; «на недостаток» - ………………

5.Для решения задачи «на недостаток» вводят

фиктивного…………………………….; задачи «на избыток» - фиктивного………………

6. Для решения ТЗ с запретами вводят вспомогательную задачу вида:

7. Для решения задачи с дополнительным ограничением xij p :