
2790
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Привыпреобразолнениибылиспсолванийедующиеьзованысоо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т- |
||||||||||||||||
ношенмеждутригонометрическимияф |
|
|
|
|
|
|
|
|
|
ункциями: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin nπ = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
sinα + sin β = 2sin |
α + β |
cos |
α − β |
. |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Систематизируполученнывыражениям |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
ao |
= 0 |
, a |
n |
= |
4E |
sin |
nπ |
|
cos |
nπ |
, b |
= 0; |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
nπ |
|
|
2 |
|
|
|
|
|
|
|
8 |
|
n |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
a2 |
+ b2 |
|
= |
|
a |
n |
|
; |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
n |
|
|
|
|
|
|
|
если a |
|
|
|
|
|||||||||
|
|
|
|
|
|
ϕn = −arctg |
bn |
|
= −arctg |
0 |
|
= |
0 |
|
|
, |
n |
> 0, |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
an |
an |
|
|
, |
|
если an < 0. |
|
|
|||||||||||||||||||||||||||||
|
Результатырасчетовоформляемвидетаблицы7. |
|
|
|
|
|
|
|
|
−π |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Таблица7 |
|
– Спектрыамплитудфаз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
n |
|
|
|
0 |
|
1 |
|
|
2 |
|
|
|
3 |
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
7 |
8 |
9 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
an |
|
|
ao |
|
= 0 |
|
3,764 |
|
0 |
|
|
|
-0,52 |
|
0 |
|
|
|
-0,312 |
|
|
|
0 |
|
|
0,538 |
0 |
-0,418 |
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
bn |
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
0 |
0 |
0 |
||||||
An |
|
|
ao |
|
= 0 |
|
3,764 |
|
0 |
|
|
|
0,52 |
|
0 |
|
|
|
0,312 |
|
|
|
0 |
|
|
0,538 |
0 |
0,418 |
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ϕn |
|
|
|
|
|
|
0 |
|
|
− |
|
|
|
-π |
|
− |
|
|
|
|
-π |
|
|
|
|
|
− |
|
|
|
|
-π |
− |
-π |
|||||||||
|
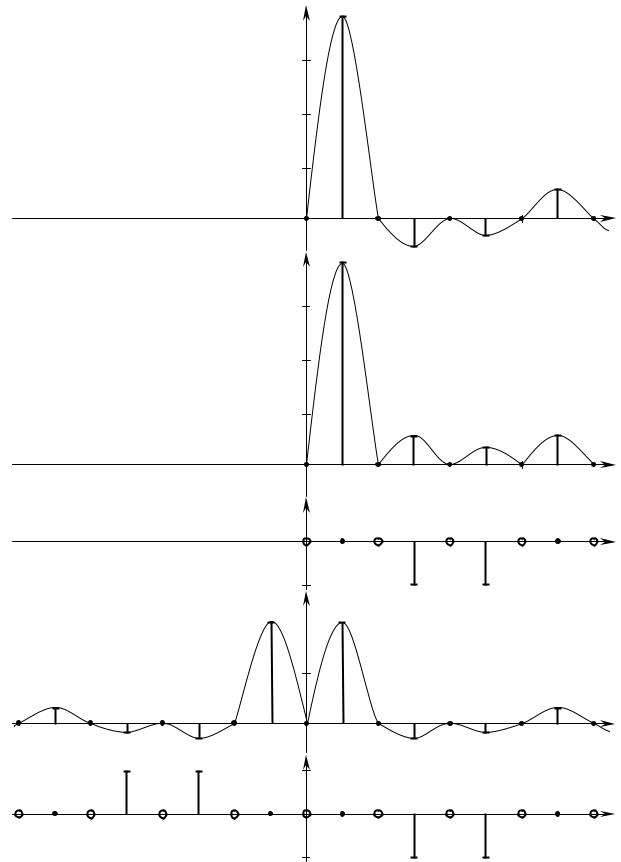
Наосновданныхт блниипркпостроениюцыступаемспектральных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
диаграмм.Нарисунке6показано.2спектральноепредставлениерассматр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ива- |
||||||||||||
емоси.гонала |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6Построе.4 оценкисигналаие
Произведема налитическвосстановлениесигналапоегоспектру. ВосстановлениепоФурьеимесл формыдующиезаписи:
sN (t) = a2o + a1 cosω1t + a2 cos 2ω1t + ... + aN cos Nω1t =
= a2o + A1 cos(ω1t + ϕ1 )+ A2 cos(2ω1t + ϕ2 )+ ... + AN cos(Nω1t + ϕ N ) =
N
= ∑Cn e jnω1t .
n=−N
Воспользунаибудвдаблееслучаенмсяформулировкойном:
sN (t ) = a2o + a1 cosω1t + a2 cos 2ω1t + a3 cos 3ω1t + ... + aN cos Nω1t
21
{an }
а) |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
3ω1 |
|
5ω1 |
8ω1 |
|
0 |
ω1 |
1 |
1 |
6ω1 7ω1 |
nω1 |
|
{An } |
|
|
|
|
|
б) |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
в) |
0 |
ω1 |
1 3ω1 |
1 5ω1 6ω1 7ω1 |
nω1 |
|
{ϕn } |
|
3ω1 |
|
5ω1 |
|
|
|
|
|
|
|
||
|
0 |
ω1 |
2ω1 |
4ω1 |
6ω1 7ω1 |
nω1 |
− π
{Сn
г) |
|
1 |
|
− ω1 0 ω1 |
nω1 |
д) |
{ϕn } |
π |
|
|
− ω1 0 |
ω1 |
nω1 |
|
− π |
|
|
Рисунок6.2 |
– Спектральнпредставлеперисиго:дическогоналаие |
|
|
|
а)спектркоэффициентов |
аn;б)спектрамплитуд |
Аn;в)спектрфаз |
ϕn;г)и |
|
д)спектркоэффициентов |
|
|
|
|
Cn и ϕn комплексногорядаФурье |
|
|||
22
при N = 5,тогда
s5 (t ) = 3,76 cosω1t + (− 0,52) cos 3ω1t + (− 0,31) cos 5ω1t ,
где ω1 = 2Tπ − угловаячастота.
Всоответствиипоследнейформулойпроизводимрасчеткомпонент оценкиихсуммы.Всюнеобходиинформацвключаеттаблую8.ица
|
|
|
|
|
|
|
|
|
T |
|
|
|
|||
Таблица8 |
– Поведеноцеи ктервалеври мени |
|
|
|
|
|
0, |
|
|
|
|
|
|||
|
|
|
4 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
t |
0 |
|
T |
|
T |
|
3 |
T |
|
T |
|
|||
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|||
|
|
|
16 |
|
|
|
16 |
4 |
|
||||||
3,764 |
cosω1t |
3,764 |
3,477 |
2,662 |
|
1,44 |
|
0 |
|
||||||
− 0,52 |
cos 3ω1t |
-0,52 |
-0,199 |
0,368 |
|
0,48 |
|
0 |
|
||||||
− 0,312 cos 5ω1t |
-0,312 |
0,119 |
0,221 |
|
-0,288 |
0 |
|
||||||||
s5 (t ) |
2,932 |
3,397 |
3,251 |
|
1,632 |
0 |
|
||||||||
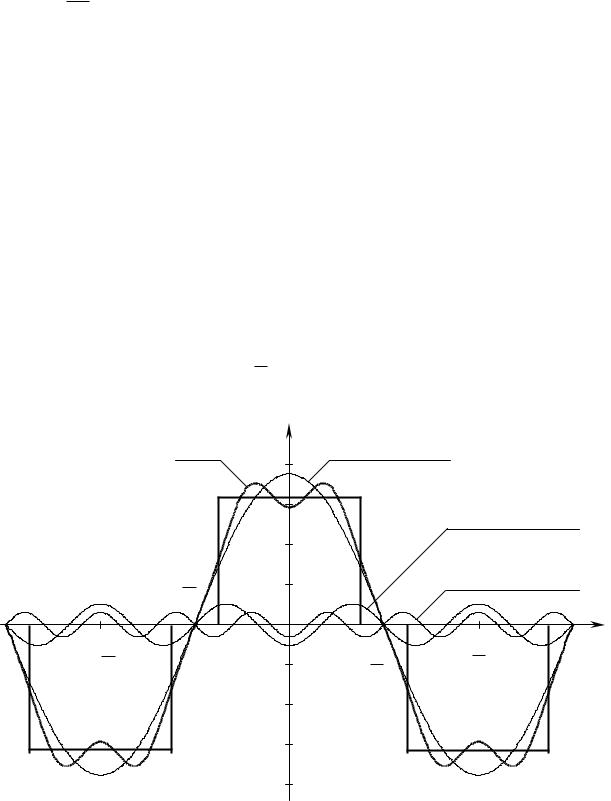
Дальнейшзависимостьграфиунюкции |
|
|
|
|
s5 (t ) отвремениможно |
|
|
определить,используясвойчетноститвоигнала |
|
|
T |
|
|
s(t ) относительнонуля |
|
нечетностиотносительноточки |
|
|
.Этонашлотражениерисунке6.3. |
|
|
||
|
|
|
4 |
|
|
|
|
|
|
s5 (t ) |
|
4 |
3,764 cosω1t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
− 0,52 cos 3ω1t |
|
|
|
|
|
2 |
|
|
|
|
− |
T |
|
1 |
|
− 0,312 cos 5ω1t |
|
|
4 |
|
|
|
|
||
T |
|
|
|
0 |
T |
T |
t |
− 2 |
|
|
|
-1 |
2 |
|
|
|
|
|
4 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
|
-4 |
|
|
|
Рисунок6.3 |
– Оценкасигнизтрехгармлаконическихлебаний |
|
|
|
|||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6Расчет.5относительногозначенияквадратасреднеквадр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а- |
|||||||||||||||||||||||||||||||||
|
|
тическойпогрешностипредставсигналаоценкойиз ения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
трехгармколебанийнических |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Если s(t ) представляетсобойнапряжение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
илиток,тогдаквадратсигн |
|
|
а- |
|||||||||||||||||||||||||||||||||||||||||
ла s2 (t ) численравемгновеннойщности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p(t),рассеиваемойнасопр |
о- |
||||||||||||||||||||||||||||||||||
тивлениенагрузкиОм1.Средняямощностьсигналапрямопропорциональна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
энергии,запасаемойпериод,обратнопроп рциональ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
напериоду: |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
t +T |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
T 2+τ 2 |
|
|
|
|
|
|
1 |
|
τ 2 |
|
|
|
1 |
|
T 2+τ 2 |
|
||||||||||||||||||||||
P = |
1 1 |
∫ s 2 (t )dt = |
|
|
|
|
|
∫ |
|
s 2 (t)dt = |
|
|
∫ E 2 dt + |
|
|
|
|
∫ E 2 dt = |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
T |
t |
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
−τ 2 |
|
|
|
|
|
|
|
T |
−τ 2 |
|
|
|
T T 2−τ 2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2E 2τ |
|
|
|
|
|
|
2 |
|
2 3,22 |
|
|
|
|||||||||||
|
1 |
|
|
|
|
τ |
|
|
τ |
|
|
T |
|
|
|
|
τ |
|
|
|
T |
|
τ |
|
|
|
|
|
|
|
2E |
|
|
|
|
||||||||||||||||||||||||
= |
|
|
|
E 2 |
|
|
|
+ |
|
|
|
+ |
|
|
|
|
+ |
|
|
|
− |
|
|
|
|
+ |
|
= |
|
|
|
|
|
|
= |
|
|
|
= |
|
|
|
|
|
|
|
|
≈ 7,68 (Вт). |
|
||||||||||
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
q |
|
8 3 |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
2 2 2 2 2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Аналогичноопредсредняямощностьляется |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n−гармоническогоси |
г- |
||||||||||||||||||||||||||||||||
нала,однакоможнопр сущизвупроестобвенноеиформулыщение:ей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Эn |
|
|
|
|
|
|
t |
+T |
|
|
|
|
|
|
|
|
|
|
t +T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
P |
|
|
|
= |
|
= |
1 |
|
|
1 |
|
|
s |
2 (t)dt = |
|
1 |
|
1 |
A2 cos |
2 (nω t + ϕ |
|
|
)dt = |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
∫ |
n |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
T |
|
|
|
|
|
T |
|
|
|
n |
|
|
|
T |
|
|
|
n |
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t1 +T |
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
∫ |
|
|
|
|
n |
[1 + cos 2(nω t + ϕ |
n |
)]dt = |
|
n |
. |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||
Уравнениепогрешностиотн( |
|
t1 |
|
|
|
|
|
|
|
|
|
|
осительноезначениеквадратасреднеква |
|
|
|
|
|
|
|
|
|
д- |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
ратическойпогрешностипредставлепериодическогоусеченнымалаия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
рядомФурье)и вид:еет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P − PN |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ = |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где PN = ∑ Pn ,причемввидуотсутпосоставляющейояннойвияможно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
n=0 |
Po = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
полагать,что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Втаблицепредставлены9 результатычисленнрасчета,исхогодным |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
длякоторогоможнсчитатьспектрам, литудолученныйпривыполнении |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
предыдущпунктовзадания. х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Наоснованализад таблииных9рисункацы6можно.4сделать |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
несколькоз |
|
амечаний.При |
|
|
|
|
|
|
|
|
n = 0 погравнаешн100чтявляо%,стьется |
|
|
|
|
|
|
|
|
|
|
|
д- |
||||||||||||||||||||||||||||||||||||
ствиемотсутпосоставляющейояннойвияспектральномописаниипр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
о- |
|||||||||||||||||||||||
цесса.Винтервалахмеждусоседнимизначен ями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
погрешностьлибоне |
|
|||||||||||||||||||||||
изменяется,либопадае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тскачкообразно,причемвеличинакаждогоскачка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
определяетсямощностьюновойгармкакникиставляющейобщоц нки

|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|||
сигнала.Помереув личения |
|
|
|
|
|
|
n относитпогрешпредставленияль остьая |
|
|
|
|
|
|||||||||||||||
сигналасуммойгарумедоникьшается.уля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Таблица9 |
– Результатырасчетапогрешности |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
n |
|
|
0 |
|
|
1 |
2 |
|
3 |
|
4 |
5 |
6 |
7 |
8 |
9 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
An ,В |
|
|
ao |
= 0 |
|
3,76 |
0 |
|
0,52 |
|
0 |
0,31 |
0 |
0,54 |
0 |
0,42 |
|||||||||||
|
|
2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pn ,Вт |
|
|
0 |
|
|
7,084 |
0 |
|
0,135 |
|
0 |
0,05 |
0 |
0,146 |
0 |
0,088 |
|||||||||||
PN ,Вт |
|
|
0 |
|
|
7,084 |
|
|
|
7,219 |
|
|
7,269 |
|
7,415 |
|
7,503 |
||||||||||
δ , % |
|
|
100 |
|
|
7,76 |
7,76 |
|
6 |
|
6 |
5,35 |
5,35 |
3,45 |
3,45 |
2,3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ, % 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9n |
|
|
|
0 |
|
1 |
|
|
2 |
|
3 |
|
|
4 |
5 |
|
|
|
6 |
7 |
|
|
8 |
|
|||||
Рисунок6.4 – Грзавфвеличинысимоспогрешностикколичества слагаемыхрядаФурье
6Определ.6 комплекснойсп ниектральнойплотности неперсигнала,совподическогоза аннымющего периодическнапротяженииодногов мода
симметричныхпределах
придругихвременах
Проведемрасчетспектральнойплотностисигнала,изображенного рисунке6.5.
Решаемзадачу,используяте спекремы.Дляэтрассмотримрахого несколькопростейшихимпульнеперныхигналов,одическихзатемпре ставимискомуюспектра льнуюплотностькаксумму.
− T2 , T2 иравногонулю
д-

25
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s(t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
τ |
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
T |
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
T |
|
t |
||||||||||||||||||
|
− |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Рисунок6.5 |
– Анализинепесигналруемыйодический |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Спектральнаяплотностьсигнала |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s1(t),изобнарисуаже6,.6,нкеного |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
известна: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eτ |
|
sin |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
(ω ) = |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
ωτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поаналогииможнозаписаспекплотностьральнуюси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гнала s2 (t ), |
|||||||||||||||
изобнарисуаже6б.Произведем.6,нкеногоеепреобразованиеспо ощью |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
формулы sin 2α = 2sinα cosα : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
sin |
ωτ |
|
|
|
|
|
|
sin |
ωτ |
cos |
ωτ |
|
|
|
|
|
|
|
sin |
ωτ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|||||||||||||||||||||||||||
|
S2 (ω) = Eτ |
|
|
|
= 2Eτ |
|
|
|
|
|
|
4 |
|
|
|
|
|
= Eτ |
4 |
|
|
|
cosω |
|
. |
|||||||||||||||||||||||||||||||||||
ωτ |
|
|
|
|
|
|
ωτ |
|
|
ωτ |
|
|
4 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Этотжерезультатможнополучить,в спольздругтехнолвавшисьй |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s3 (t ). |
|
|
|
о- |
|||||||||||||||||||||||||||
гией,примененнойдляспектральногоан |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
алсизагнала |
|
|
|
|
||||||||||||||||||||||||||||||||||
26
|
|
|
s1(t ) |
|
|
|
s2 (t ) |
|
|
|
|
E |
|
|
|
E |
|
|
|
|
|
τ 2 |
|
|
|
τ |
|
|
|
|
|
τ |
τ |
|
|
|
|
|
|
|
− |
|
||
|
|
|
|
|
4 |
4 |
|
|
− |
τ |
0 |
τ |
t |
τ |
0 |
τ |
t |
4 |
|
4 |
− |
2 |
|
2 |
|
|
|
|
|
а) |
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s3 (t ) |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
T |
|
|
τ |
|
|
|
|
|
T |
− |
τ |
|
|
||||||||||||||
|
|
|
− |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
4 |
2 |
4 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
− |
T |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
t |
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
τ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
τ 2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− E |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
|
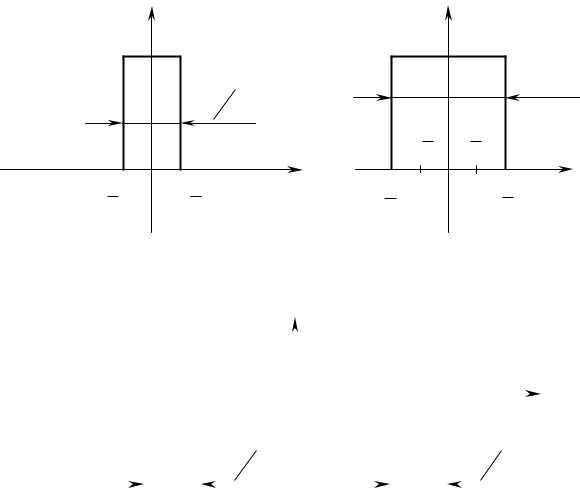
Рисунок6.6 |
– Элементарсоставляющиесигналаые |
|
s(t ) = s2 (t )+ s3 (t ) |
|
|||
Сигнал s3 (t ) образовансуммойдвухсигвидаалов |
T |
s1(t ),одинизкот |
о- |
||||
|
|
|
τ |
|
|||
рыхсдвправоинут,другой |
− влевонавеличину |
t = |
|
− |
|
,чтояснови |
д- |
2 |
|
||||||
нонарисунке6в.Применяя.6,т оремусдвигате взвешенномремусу |
|
|
4 |
м- |
|||
|
|
|
|
|
|||
мир,пованлучим |
|
|
|
|
|
|
|
|
|
|
|
|
ωτ |
|
||
|
|
Eτ |
|
sin |
|
|
|
|
S3 |
(ω)= − |
4 |
|
|||||
2 ωτ |
|
|||||||
|
|
|
||||||
|
|
4 |
|
|
||||
|
T |
τ |
|
||
e |
jω |
|
− |
|
|
|
|
||||
|
2 |
4 |
+ e |
||
|
|
|
|
|
|
T |
τ |
|
|
|
||
− jω |
|
− |
|
|
|
= −Eτ |
|
|
|||||
|
2 |
4 |
|
|||
|
|
|
|
|
|
|
sin |
ωτ |
|
T |
|
|
|
|
|||
|
|
|
|
τ |
|
|||||
4 |
|
|
||||||||
|
cosω |
|
− |
|
|
. |
||||
ωτ |
|
2 |
4 |
|||||||
|
|
|
|
|||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Такимобразом,сигнал |
s(t ) имеспектральнуюп |
|
|
|
|
|
|
|
лотность: |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
sin |
ωτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
|
|
|
τ |
|
||||||||||
S(ω )= S2 |
(ω )+ S3 (ω )= Eτ |
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
cosω |
|
|
|
− cosω |
|
− |
|
|
|
. |
|||||||||||||||||||||
|
|
ωτ |
|
4 |
|
4 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
α + β |
|
|
|
β −α |
|
|
|||||||||||||
Воспользовавшисьформулой |
|
cosα − cosβ = 2sin |
sin |
|
,получим |
||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
ωτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
sin |
|
|
|
|
T |
|
|
|
|
T − τ |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
S(ω) = 2Eτ |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
sinω |
|
sinω |
|
|
|
|
. |
|
|
|
|
|
||||||||||||||||||
|
|
|
4 |
|
4 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
ωτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4
Проведпровполученногормезультатаку:
1. Спектральнаяплотность – действительнаяфункциячастоты,.. мнимаясоставляравнанул. ющая
2.S(ω = 0) = 0 (структурасигналатакова,чтосуммарнаяплощадьпод еговременграфикомравнаулю)ым.
3.Размерность [S(ω)]= В с.
6Построение.7 графикамодуляспектральнойплотности
фазовогоспектранеперигналаодического |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Приведвыражениесп м |
|
|
|
|
|
ктральнойплотностиви,удобномудля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
построенияграфика: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
ωτ |
|
|
|
T |
|
|
|
|
T − τ |
|
|
|
|
|
sin |
ωτ |
|
|
|
|
q |
|
|
|
q −1 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
S(ω) = 2Eτ |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
sinω |
|
sinω |
|
|
|
|
|
= 2Eτ |
|
|
sinωτ |
|
|
|
sinωτ |
|
|
|
|
= |
|||||||||||||||||||||||||
ωτ |
|
|
4 |
4 |
|
|
ωτ |
|
|
4 |
|
|
4 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
ωτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
= 2Eτ |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
sin |
|
ωτ |
sin |
|
ωτ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
ωτ |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Анализиполученноевырсучетомуяажение |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin nπ |
|
0 |
для |
n |
|
|
0,1,2,... |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
= |
|
|
|
, |
||||||||||||
полуто,вкоторыхчкиаемграфикфун ции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
S(ω) пересекаетчастоось ную |
|
|
|
|
|
|
|
||||||||||||||||||
(нулифункции): |
|
|
|
|
2 |
ωτ = nπ |
ω = |
3π |
n; |
|
ωτ = nπ |
|
|
ω = |
|
12π |
n.Ктомуже |
|
|
||||||||||||||||||||||||||||
|
|
|
|
3 |
2τ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
нанулевойчастоте |
|
|
|
|
S(ω)= 0. |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
5τ |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Необходимовыбрашаг,скобудеторымьпроизводитьсяменение аргументафункции.Дляэтогоподходитполовинаинтермеждудвумяала

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
нулями,которыенаходятсяминимальномрасстояниидруготдруга.И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с- |
|||||||||
пользуемследующзначениячастоты: |
|
|
|
|
|
|
|
3π |
|
|
|
6π |
|
|
|
|
|
12π |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
ωʹ = |
2 = |
|
; ωʹʹ = |
. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2τ |
|
2τ |
|
|
|
5τ |
|
|
|
|
|
||||||||||||
Тогдашагравен: |
|
h = |
ωʹ −ωʹʹ |
= |
|
|
6π 2τ −12π 5τ |
|
= 0,3 |
π |
. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
|
|||||||||||||
|
Передпостроенирезультарасчпредставитьудобномывиде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б- |
|||||||||
лицы10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таблица10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ωτ |
|
|
|
( ) |
|
|
ωτ |
|
|
|
|
|
( ) |
|
|
|
|
ωτ |
|
|
|
( ) |
||||||||||||
|
|
|
|
|
S |
ω |
|
|
|
|
|
|
|
|
|
|
|
S |
|
ω |
|
|
|
|
|
|
|
|
S |
ω |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
π |
|
|
2Eτ |
|
|
|
|
|
π |
|
|
|
|
2Eτ |
|
|
|
|
|
|
π |
|
|
2Eτ |
|
||||||||
0,3 |
|
|
0,22 |
|
|
|
|
2,7 |
|
|
|
0,09 |
|
|
|
|
5,1 |
|
0,07 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
0,6 |
|
|
0,65 |
|
|
|
|
3 |
|
|
|
|
|
|
|
0 |
|
|
|
|
5,4 |
|
0,14 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
0,9 |
|
|
0,81 |
|
|
|
|
3,3 |
|
|
|
-0,11 |
|
|
|
5,7 |
|
0,12 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1,2 |
|
|
0,5 |
|
|
|
|
3,6 |
|
|
|
-0,1 |
|
|
|
|
6 |
|
|
|
0 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1,5 |
|
|
|
|
0 |
|
|
|
|
3,9 |
|
|
|
|
|
|
0 |
|
|
|
|
6,3 |
|
-0,11 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1,8 |
|
|
-0,29 |
|
|
4,2 |
|
|
|
0,02 |
|
|
|
|
6,6 |
|
-0,12 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2,1 |
|
|
-0,22 |
|
|
4,5 |
|
|
|
|
|
|
0 |
|
|
|
|
6,9 |
|
-0,05 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2,4 |
|
|
|
|
0 |
|
|
|
|
4,8 |
|
|
|
|
|
|
0 |
|
|
|
|
7,2 |
|
|
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
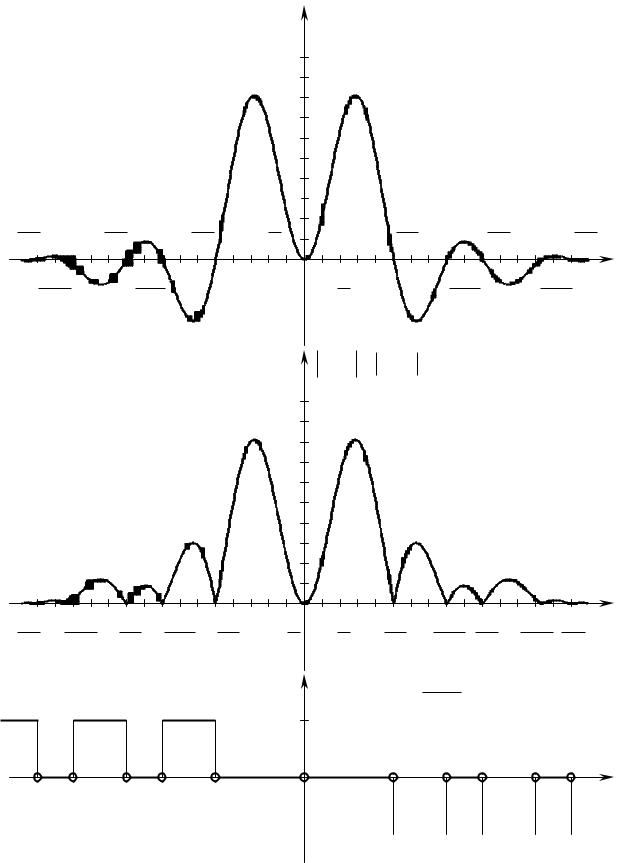
Нарисунке6аизображена.7, |
пектральплотностьисследуемогоая |
е- |
прерывнонеперсигодическогонала |
S(ω)= A(ω).Нарисунке6бв.п7, |
о- |
казанымодульамплитудно( |
-частотнаяхарактеспектра)и гументистика |
|
(фазо -частотнаяхарактеристиспектральнойспектра)комплексной |
лотно- |
|
сти. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(ω)= A(ω) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2Eτ |
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
9π |
|
|
− |
6π |
|
|
− |
3π |
− 0,3π |
|
|
|
3π |
|
6π |
9π |
|
||
|
2τ |
|
|
|
2τ |
|
|
|
2τ |
|
τ |
|
|
|
2τ |
|
2τ |
2τ |
|
|
|
− |
24π |
|
|
− |
12π |
|
|
|
|
0 |
0,3 |
π |
|
12π |
24π |
ω |
|||
|
5τ |
|
|
|
|
5τ |
|
|
|
|
|
τ |
|
5τ |
5τ |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(ω) = A(ω) |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2Eτ |
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
− |
9π |
− |
24π |
− |
6π |
− |
12π |
− |
3π |
− 0,3 |
π |
0,3 |
π |
3π 12π 6π 24π 9π ω |
||||||
2τ |
|
5τ |
2τ |
5τ |
2τ |
τ |
τ |
2τ |
5τ 2τ |
5τ 2τ |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
в) |
|
|
|
|
|
|
|
|
|
|
ϕ(ω) = −arctg |
0 |
0 |
, если A(ω) > 0, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
A(ω) |
−π , если A(ω) < 0. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
Фаза – нечетнаяфункциячастоты |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
9π |
|
24π |
6π |
12π 3π |
0 |
|
|
3π |
|
12π 6π 24π 9π |
|
ω |
|||||||||||||||
− |
|
− |
|
− |
|
− |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2τ |
5τ |
2τ |
5τ |
2τ |
|
|
− π |
2τ |
|
|
5τ 2τ |
|
|
5τ 2τ |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок6.7 |
– Зависимостьспектральнойплотности)(модуляспектральной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
плотностиб()фазоспектрав()неперого сичастотыгналаодического |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
