
1585
.pdf41
СТАТИСТИЧЕСКАЯ МОДЕЛЬ ВЕКТОРНОГО РАДИОЛОКАЦИОННОГО СИГНАЛА
Построение модели поля сводится к принятию ряда предположений о законах распределения его составляющих. Знание законов распределения позволяет связать статистические характеристики при различных способах описания поля, а также получить недостающие моменты составляющих и параметры законов распределения по имеющимся (как правило, весьма ограниченным) опытным данным.
Реальное электромагнитное поле радиолокационного сигнала представляет собой случайную векторную функцию векторного же аргумента. Эта функция имеет две ортогональные составляющие в выбранном поляризационном базисе. Напряженность поля
поперечной волны |
|
G |
G |
jωt |
e |
jϕm |
G |
|
jωt |
e |
jϕc |
) . |
|
|
|
|
(1) |
||||||||||
Здесь xGm и |
xGc |
ε = xm Em Re( e |
|
|
) + xc Ec Re( e |
|
|
||||||
- орты составляющих соответственно основной и кросс-поляризации |
|||||||||||||
сигнала, перпендикулярные направлению распространения волны. В качестве xGm и xc могут |
|||||||||||||
рассматриваться орты любых двух ортогональных составляющих поля. |
|
||||||||||||
Вектор комплексных амплитуд составляющих |
|
|
|
|
|
|
|||||||
|
|
|
→ |
|
• |
|
|
|
|
|
|
|
|
|
|
|
• |
Em |
, |
|
|
|
|
|
(2) |
||
|
|
|
E = |
• |
|
|
|
|
|
|
|||
|
|
|
|
E c |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
• |
= Ec e jϕc - |
|
|
|
|
|
|
|
|
|
|
|
где E m = Eme jϕm ; E c |
узкополосные |
|
во |
времени |
процессы, поскольку |
ширина |
|||||||
временного спектра флуктуаций, возникающих при распространении и отражении сигнала, значительно меньше частоты ω.
В большинстве реальных случаев (в частности, при приеме радиоимпульсов) сигнал дополнительно модулирован по амплитуде. Кроме того, зондирующие радиолокационные сигналы могут быть модулированы по частоте или пространству (например, при использовании РЛС с ЧМ или при наличии протяженных или движущихся источников). Однако в случае, когда период этой модуляции значительно меньше времени корреляции флуктуаций, возникающих в радиолокационном канале, а среда является линейной, сигнал можно считать немодулированным, относя результаты анализа структуры поля к определенному уровню модуляции. Таким образом, будем считать источник излучения точечным, неподвижным и монохроматическим. Такое приближение допустимо, если величина, обратная ширине спектра модуляции сигнала, составляет не более 30-40% радиуса корреляции передаточной функции радиолокационного канала по соответствующему аргументу.
Векторный аргумент случайного поля r включает в себя, прежде всего, пространственные координаты точки наблюдения x, y, z и время t. Кроме этого, в число аргументов могут быть включены аналогичные величины, характеризующие свойства излучателя, а также частота f. Могут быть использованы и такие аргументы, как ширина диаграммы направленности передающей и/или приемной антенн, их ориентация и др.
Примем следующие предположения для рассматриваемой модели поля:
•поле является аддитивной смесью регулярной и случайной составляющих,
•случайная составляющая поля является гауссовой функцией с нулевым средним, стационарной по всем своим аргументам.
Известно [1], что при сделанных предположениях ортогональные квадратурные
•
компоненты аналитических сигналов E распределены по нормальному закону, имеют равные дисперсии и некоррелированы при совпадающих значениях аргументов, амплитуды распределены по обобщенному закону Рэлея, а фазы случайных составляющих равномерны в интервале ±π.

42
Рассматриваемая модель поля, которая может быть названа нормальной моделью, хорошо согласуется с представлением об отражении сигнала от большинства реальных радиолокационных целей, имеющих сложную структуру и размеры, существенно превышающие длину волны. При этих условиях цель обычно рассматривается как совокупность многих независимых «светящихся» точек, и в силу центральной предельной теоремы теории вероятностей распределение суммы сигналов от этих точек можно считать гауссовым. В то же время выделение регулярной составляющей открывает возможность применения модели в случае, когда один из отражателей (рассеивателей) является преобладающим.
Сделанные предположения дополнительно оправдываются следующим обстоятельством. Применение условных функций распределения и использование регулярной составляющей поля в качестве параметра этих распределений часто позволяет ограничиться обоснованием сделанных предположений только для быстрых и мелкомасштабных флуктуаций поля, периоды которых не превышают интервалов измерений в реальных радиотехнических системах: во времени - нескольких секунд и в пространстве - нескольких метров или десятков метров.
Таким образомG |
,Gнапряженность поля |
|
|
|
|
|
|||||
ε |
= xm Em cos(ωt +ϕm ) + xc Ec cos(ωt +ϕc ) = |
|
|
||||||||
|
G |
|
|
|
|
G |
|
|
|
|
|
= xm (Em cos cosωt − Em sin sinωt) + xc (Ec cos cosωt − Ec sin sinωt) = |
|||||||||||
= xGm (εmreg +εmran ) + xGc (εcreg +εcran ) = |
|
|
|
|
|||||||
= xGm [Emreg cos(ωt +ϕmreg ) + Emran cos(ωt +ϕmran )]+ |
(3) |
||||||||||
+ xGc [Ecreg cos(ωt +ϕcreg ) + Ecran cos(ωt +ϕcran )]= |
|
||||||||||
= xGm [(Emreg cos + Emran cos ) cosωt − (Emreg sin + Emran sin ) sinωt]+ |
|||||||||||
+ xG |
(E |
creg cos |
+ E |
cran cos |
) cosωt − (E |
creg sin |
+ E |
cran sin |
) sinωt . |
||
|
c [ |
|
|
|
|
|
] |
||||
Здесь для каждой из составляющих, обозначенных индексами m - main (основная поляризация) и c - cross (кросс-поляризация) применены обозначения:
Ecos = E cosϕ = Ereg cos + Eran cos ; Esin = E sinϕ = Ereg sin + Eran sin ;
Ereg cos = Ereg cosϕreg ; Ereg sin = Ereg sinϕreg ; Eran cos = Eran cosϕran ; Eran sin = Eran sinϕran ;
E = |
Ecos2 |
+ Esin2 = (Ereg cos + Eran cos )2 |
+(Ereg sin + Eran sin )2 |
= |
|
||||||
= |
Ereg2 + Eran2 |
+ Ereg Eran cos(ϕreg −ϕan ); |
|
|
|
||||||
ϕ = arctg |
|
E |
sin |
= arctg |
Ereg sin + Eran sin |
|
= arctg |
Ereg sinϕreg |
+ Eran sinϕran |
. |
|
|
Ecos |
Ereg cos + Eran cos |
Ereg cosϕreg |
+ Eran cosϕran |
|||||||
|
|
|
|
|
|
||||||
Все величиныG E и ϕ c различными индексами являются функциями векторного аргумента r = {t, x, y, z, f,...}.
Нормальное стационарное векторное поле полностью определяется своей двумерной плотностью вероятности, а она, в свою очередь, - регулярной составляющей и матрицей ковариантных функций
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43 |
||||
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
Bεm ( r ) |
Bεmc ( r ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
Bε ( r ) = |
B |
( rG) |
|
B |
|
( rG) |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
rG) cos ωG |
|
|
|
|
|
|
εcm |
]G |
|
|
|
εc |
|
|
|
|
|
ωG |
|
|
|
|
|
|
] |
|
|
|
(4) |
|||
= |
|
f |
|
( |
rG + |
α |
|
|
( rG) |
|
f |
|
|
( |
rG) cos |
rG +α |
|
|
( rG) |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
f |
|
|
εm |
|
G |
|
[ G |
G |
|
|
εm |
|
(− |
] |
|
εmc |
( |
G |
[G |
G |
+α |
εmc |
G |
] |
|
|
|
. |
||||||||||
|
εmc |
(− |
|
r ) cos |
−ω |
r |
+α |
εmc |
r ) |
|
f |
εc |
r ) cos |
ω |
r |
εc |
( |
r ) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
[ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ |
|
|
|
|
|
|
|
|
|
||||||||
Здесь f и α - соответственно модуль и фаза ковариантных функций: отдельных составляющих (с индексами m и c) и взаимной ковариантной функции (с индексом mc). Под вектором rGпонимается совокупность приращений аргументов поля { t, x, y, z, f,...}. Векторная частота ω представляет собой совокупность аргументов кратного преобразования Фурье поля по всем переменным, то есть спектральной плотности поля, а скалярное произведение ω r = ωt t + ωx x + ...
Двумерная плотность распределения квадратурных составляющих
W(EG,rG, rG) =
где
Em cos (r )Em sin (rG)Em cos (rG +
G = Em sin (rG +
E Ec cos (GrG)
Ec sin (r )Ec cos (rG +Ec sin (rG +
|
[ |
~G |
~G |
|
G |
|
|
G |
|
|
], |
|
exp − (E |
− M E )BE−1 (E |
|
− |
M E ) / 2 |
|
|
||||||
|
|
(2π)4 (det BE )1/2 |
|
|
|
|
|
|||||
|
|
|
Emreg cos (r ) |
|
|
|
|
|
||||
G |
|
|
E |
|
(rG) |
G |
|
|
|
|
||
|
|
|
mreg sin |
G |
+ |
|
|
|
|
|||
r ) |
|
Emreg cos (r |
|
r ) |
|
|
|
|||||
G |
|
G |
|
|
G |
|
+ |
G |
|
|
|
|
r ) |
Emreg sin |
(r |
|
r ) |
|
|
|
|||||
|
; M E |
= Ecreg cos |
(rG) |
|
|
; |
|
|
||||
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
Ecreg sin |
(r ) |
|
|
|
|
|
|||
rG) |
|
Ecreg cos |
(rG |
|
+ |
rG) |
|
|
|
|||
G |
|
|
|
|
G |
+ |
G |
|
|
|
|
|
r ) |
|
Ecreg sin |
(r |
r ) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(5)
(6)
|
|
1 |
|
0 |
|
ρ |
m |
( |
rG) |
λ |
|
( |
rG) |
|
ηρ |
mc |
(0) |
ηλ |
|
(0) |
ηρ |
mc |
( |
|
rG) |
||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
0 |
|
1 |
|
|
|
G |
m |
|
|
|
G |
|
|
|
(0) |
|
mc |
(0) |
|
|
|
|
|
G |
|||||||||
|
|
|
|
−λ |
( r ) |
ρ |
m |
( r ) |
|
−ηλ |
|
|
ηρ |
mc |
−ηλ |
|
( r ) |
||||||||||||||||||
|
|
G |
|
|
G |
|
|
m |
|
|
|
|
|
|
|
|
|
mc |
G |
|
|
G |
|
|
|
mc |
|
|
|||||||
|
|
ρm ( r ) |
−λm ( r ) |
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
ηρmc (− |
r ) |
ηλmc (− |
r ) |
ηρmc (0) |
||||||||||||||
G |
= σ 2 |
λm ( rG) |
ρm ( rG) |
|
|
|
0 |
G |
|
|
|
1 |
|
|
G |
−ηλmc (− rG) ηρmc (− rG) |
−ηλmc |
(0) |
|||||||||||||||||
BE |
ηρmc (0) |
−ηλmc (0) |
|
|
|
|
−ηλmc (− |
η |
2 |
|
|
0 |
|
|
η |
2 |
ρc |
( |
G |
||||||||||||||||
|
|
ηρmc (− r ) |
r ) |
|
|
|
|
|
|
|
r ) |
||||||||||||||||||||||||
|
|
ηλmc (0) |
ηρmc (0) |
ηλmc (− rG) |
ηρmc (− rG) |
|
0 |
|
|
η2 |
|
−η2 λc ( rG) |
|||||||||||||||||||||||
|
|
ηρmc ( rG) −ηλmc ( rG) |
|
ηρmc (0) |
−ηλmc (0) |
η2 ρc ( rG) |
−η2 λc ( rG) |
|
|
|
η2 |
|
|||||||||||||||||||||||
|
|
ηλ ( rG) |
ηρ |
mc |
( rG) |
|
ηλ (0) |
ηρ |
mc |
(0) |
|
η2 λ ( rG) |
η2 ρ |
( rG) |
|
|
|
0 |
|
|
|||||||||||||||
|
|
mc |
|
|
|
|
|
mc |
|
|
|
|
|
|
|
|
c |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Здесь |
σ2 = σm2 cos = σm2 sin |
= Emran2 |
cos = Emran2 |
sin |
|
- дисперсия |
|
квадратурных |
|||||||||||||||||||||||||||
ηλ ( |
rG) |
|
|
|
|
|
|||
mc |
G |
|
|
|
ηρmc ( r ) |
|
|
|
|
ηλmc (0) |
|
|
|
|
ηρmc (0) |
|
|
.(7) |
|
η2 λc ( rG) |
|
|
||
η2 ρc ( |
rG) |
|
|
|
0 |
|
|
|
|
η2 |
|
|
|
|
компонентов
напряженности поля основной поляризации;
|
|
|
|
|
|
|
σc2cos = σc2sin = Ecran2 |
cos = Ecran2 |
sin - дисперсия квадратурных компонентов напряженности поля |
||||
кросс-поляризации; |
|
|
||||
η2 = σc2cos / σm2 cos = σc2sin / σm2 sin ;
ρm, λm, ρc, λc, ρmc, λmc - нормированные авто- и взаимные ковариантные функции составляющих вектора напряженности поля, определяемые равенствами:
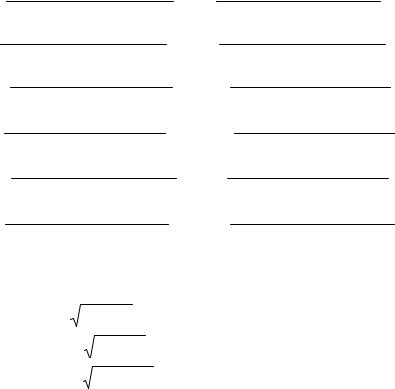
ρ ( rG) |
= |
|
1 |
|
|
|
E |
|
|
|
|
|
|
|
|
|
(rG)E |
|
|
|
|
|
|
|
|
(rG + |
|
|
|
rG) |
= |
|
1 |
|
E |
|
|
|
|
|
|
|
(rG)E |
|
|
|
|
|
(rG |
+ rG); |
||||||||||||||||||||||||||||||||||||||||||
|
σ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
mran cos |
|
|
|
|
|
|
|
|
|
|
mran cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mran sin |
|
|
|
|
|
|
|
mran sin |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
λ ( rG) = |
|
1 |
|
E |
|
|
|
|
|
|
|
|
|
(rG)E |
|
|
|
|
|
|
|
|
(rG |
+ |
|
|
rG) |
|
= − |
|
1 |
|
|
|
E |
|
|
|
|
|
|
|
(rG)E |
|
|
|
|
|
(rG + rG); |
|||||||||||||||||||||||||||||||||||||||||||
σ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
m |
|
|
|
|
|
|
|
|
|
mran cos |
|
|
|
|
|
|
|
|
mran sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mran sin |
|
|
|
|
|
|
|
mran cos |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
ρ ( rG) |
= |
|
|
|
|
1 |
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
(rG)E |
|
|
|
|
|
|
(rG + |
|
|
rG) |
= |
|
|
|
|
|
1 |
|
|
|
|
|
E |
|
|
|
|
|
|
(rG)E |
|
|
|
|
(rG + rG) |
; |
|
||||||||||||||||||||||||||||||||||
|
η2σ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η2σ 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
c |
|
|
|
|
|
|
|
|
cran cos |
|
|
|
|
|
|
|
|
|
|
cran cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cran sin |
|
|
|
|
|
|
|
|
cran sin |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
λ ( rG) = |
|
|
|
|
|
1 |
|
|
|
E |
|
|
|
|
|
|
|
|
(rG)E |
|
|
|
|
|
|
|
(rG |
+ |
|
|
|
rG) |
|
= − |
|
|
|
|
|
1 |
|
|
|
|
E |
|
|
|
|
|
|
(rG)E |
|
|
|
|
(rG + rG) |
; |
||||||||||||||||||||||||||||||||||
η2σ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η2σ 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
c |
|
|
|
|
|
|
cran cos |
|
|
|
|
|
|
|
|
|
cran sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cran sin |
|
|
|
|
|
|
|
|
cran cos |
|
|
|
|||||||||||||||||||||||||||||||||||||||
ρ ( rG) = |
|
1 |
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
(rG)E |
|
|
|
|
|
|
(rG + |
|
|
rG) |
= |
|
|
|
|
|
1 |
|
|
|
|
E |
|
|
|
|
|
|
|
(rG)E |
|
|
|
|
(rG + rG) |
; |
|
||||||||||||||||||||||||||||||||||||||
|
ησ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ησ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
mc |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
mran cos |
|
|
|
|
|
|
|
|
|
|
cran cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
mran sin |
|
|
|
|
|
|
|
|
cran sin |
|
|
|
|
|||||||||||||||||||||||||||||||||
λ ( rG) |
= |
|
|
|
|
1 |
|
|
|
E |
|
|
|
|
|
|
|
|
|
(rG)E |
|
|
|
|
|
|
|
(rG |
+ |
|
|
|
rG) |
= − |
|
|
|
|
1 |
|
|
|
|
E |
|
|
|
|
|
|
|
(rG)E |
|
|
|
|
(rG + rG); |
|||||||||||||||||||||||||||||||||||
|
|
ησ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ησ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
mc |
|
|
|
|
|
|
|
|
|
mran cos |
|
|
|
|
|
|
|
|
|
cran sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mran sin |
|
|
|
|
|
|
|
|
cran cos |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρm (0) = ρc (0) = 1; λm (0) = λc (0) = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Учитывая эти соотношения, легко показать, что в матрице (4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
εm |
|
= σ2 |
|
|
|
|
ρ2 |
|
+ λ2 |
|
;α |
εm |
|
= arctg(λ |
|
|
/ ρ ); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
εc |
= |
σ2η2 |
|
|
|
ρ2 |
|
+ |
λ2 |
; |
α |
εc |
|
= arctg( |
λ |
|
|
/ |
ρ ); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
εmc |
|
= σ2η |
|
|
|
ρ2 |
|
|
+ |
λ2 |
|
|
;α |
εmc |
= arctg(λ |
|
|
/ ρ |
mc |
) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mc |
|
|
|
|
|
mc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
и, следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
= |
|
|
|
|
|
f |
|
|
|
|
|
|
|
cosα |
|
|
; λ |
|
|
= |
|
|
|
|
|
|
|
f |
|
|
|
|
sinα |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
σ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
εm |
|
|
|
|
|
|
|
εm |
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
εm |
|
|
|
|
|
|
|
εm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
= |
|
|
|
|
|
1 |
|
|
|
|
|
f |
|
|
cosα |
|
|
;λ = |
|
|
1 |
|
|
|
|
f |
|
|
|
sinα |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ 2η |
|
|
|
|
|
|
|
|
σ2η2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
2 |
|
|
|
|
|
|
εc |
|
|
|
|
|
|
|
εc |
|
|
|
c |
|
|
|
|
|
|
|
|
εc |
|
|
|
|
|
|
|
εc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
= |
|
|
|
|
1 |
|
|
|
|
f |
|
|
|
cosα |
|
|
|
|
; λ |
|
|
|
= |
|
|
|
|
1 |
|
|
|
f |
|
|
|
|
|
sinα |
|
|
|
|
. |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ 2η |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ 2η |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mc |
|
|
|
|
|
|
|
|
|
|
εmc |
|
|
|
|
|
|
|
εmc |
|
|
|
mc |
|
|
|
|
|
|
|
εmc |
|
|
|
|
|
|
|
εmc |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
44
(8)
(9)
Таким образом, для полной характеристики векторного поля должны использоваться следующие его параметры.
1. |
Мощность |
P = (Emreg2 / 2) +σ2 , характеризующая общую мощность (энергию) поля |
сигналов основной поляризации. Эту величину можно считать не зависящей от r . |
||
2. |
Отношение |
мощности регулярной и случайной составляющих поля основной |
поляризации g2 = Emreg2 / (2σ2 ) . Эту важную величину, которая может в значительной
степени характеризовать когерентность сигнала, также можно считать не зависящей от r .
3. Фаза регулярной составляющей поля основной поляризации ϕmreg (r ). В наиболее интересном случае плоской волны регулярной составляющей вместо ϕmreg (r ) целесообразно использовать величину разности фаз
|
G |
|
G |
|
G |
|
G |
2π |
|
|
|
|
|
|
ϕ ( |
r ) = ϕ |
|
(r |
+ |
r ) −ϕ |
|
(r ) = |
|
( x sinα |
|
cosβ + |
y cosα |
cosβ + |
z sin β ). (10) |
|
|
λ |
|
|||||||||||
mreg |
|
mreg |
|
|
|
mreg |
|
|
m |
m |
m |
m |
m |
|
|
|
|
|
|
|
|
Здесь αm и βm - углы прихода плоской волны основной поляризации в горизонтальной и вертикальной плоскостях: αm - азимут относительно оси y, βm - угол места относительно плоскости x0y; x, y, z - разнесение точек приема по осям координат.
4.Отношение мощности регулярных составляющих кросс- и основной поляризации
ξ2 = Ecreg2 / Emreg2 , η2 - то же для случайных составляющих.
5.Фаза регулярной составляющей кросс-поляризации ϕcreg (r ) и связанные с ней
величины ϕcreg , αc и βc . Обычно можно считать, что углы прихода регулярных

45
составляющих основной и кросс-поляризации одинаковы: αm = αc = α ; βm = βc = β. В этом случае ϕmreg ( r ) = ϕcreg ( r ) . Однако, в общем случае следует считаться с тем, что углы прихода могут быть различными.
6. Разность фаз регулярных составляющих основной и кросс-поляризации при совпадающих значениях аргументов ψ = ϕmreg (r ) −ϕcreg (r ) . При αm ≠ αc и βm ≠ βc величина ψ зависит от rGи поле, вообще говоря, нельзя считать стационарным. Однако, если нестационарность вызвана только этим обстоятельством, то поле может иметь стационарные приращения и рассматриваемая модель остается справедливой (см. также далее, п. 10). При проведении практических расчетов следует либо принимать ψ = 0, либо считать эту величину для любой точки наблюдения (например, для r = 0) равновероятной в интервале ±π с нулевым средним, а в других точках вычислять ψ( r ) по формуле, полученной вычитанием двух выражений (10), в первое из которых подставляются величины αm , βm , а в другое - αc , βc .
7. Модули нормированных коэффициентов корреляции случайных составляющих
основной и кросс-поляризации
f m ( rG) = fεm ( rG) / σ 2 ; f c ( rG) = fεc ( rG) / (σ 2η2 ).
Будем полагать, что корреляционные функции факторизуются и могут быть аппроксимированы произведениями гауссовых кривых по отдельным аргументам. При αm =
αc = βm = βc = 0
fm (
fc (
rG)
rG)
|
|
x |
2 |
|
z |
|
2 |
|
|
t |
|
2 |
|
|
f |
|
|
2 |
|
|
||||||
= exp− |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
+ |
|
|
|
+ |
|
|
|
|
+ |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|||||||||||||
|
d0m |
|
z0m |
|
|
τ0m |
|
|
f0m |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11) |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
x |
|
|
z |
|
|
t |
|
|
f |
|
|
|
|
|
||||||||||
= exp− |
|
|
|
|
|
+ |
|
|
|
+ |
|
|
|
+ |
|
|
|
; |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
d0c |
|
|
z0c |
|
|
τ0c |
|
f 0c |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где d0 - поперечный к трассе горизонтальный пространственный радиус огибающей функции корреляции на уровне 1/e; z0, τ0, f0 - соответственно высотный, временной и частотный радиусы корреляции, второй индекс означает вид поляризации. Продольный интервал корреляции при малой ширине углового спектра рассеянных сигналов (что типично для радиолокации) много больше поперечного, поэтому соответствующий член в выражениях (11) отсутствует.
При αm , αc , βm , βc , отличающихся от нуля (что равносильно повороту системы координат) радиусы корреляции вдоль осей x и z обратно пропорциональны косинусам соответствующих углов (кроме малых участков углов вблизи 90 градусов) [2], поэтому выражения (11) принимают вид
fm ( rG) = exp−
fc ( rG) = exp−
|
2 |
|
x cosαm |
+ |
|
d0m |
|
|
|
2 |
|
x cosαc |
+ |
|
d0c |
|
|
z cosβm |
|
2 |
|
|
t |
|
|
+ |
|
|
|||
z0m |
|
|
|
|
τ0m |
|
|
2 |
|
|
t |
|
|
z cosβc |
|
+ |
|
|
||
z0c |
|
|
|
τ0c |
||
|
2 |
|
|
f |
|
|
2 |
|
|
+ |
|
|
|
; |
|||||
|
|
|
|
|
|
||||
|
|
f0m |
|
|
|
||||
|
|
|
|
|
|
|
|
|
(12) |
2 |
|
|
f |
|
2 |
|
|||
|
|
|
|||||||
|
+ |
|
|
|
. |
|
|
||
|
|
|
|
|
|
||||
|
|
f0c |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
8. Модуль нормированного коэффициента взаимной корреляции случайных составляющих основной и кросс-поляризации f mc ( rG) = fεmc ( rG) / (ησ 2 ) . Будем полагать,
что при αm ≈ αc ≈ βm ≈ βc ≈ 0 взаимная корреляционная функция, как и для отдельных компонентов поля, аппроксимируется произведением гауссовых кривых, но сдвинутых относительно нулевых значений аргументов на некоторые величины δx, δz, δt, δf. Тогда формула (12) перепишется в виде:
|
|
G |
|
|
|
x cosα |
−δx |
2 |
|
|
|
|
|
|
|
|
|||||
f |
mc |
( r ) = R |
max |
exp− |
|
d0mc |
|
|
|
+ |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
z cosβ |
−δz 2 |
|
t −δt |
2 |
|
f −δf |
|
2 |
|
|
|
|
|
+ |
|
+ |
|
|
. (13) |
||
z0mc |
|
|
|
|||||||
|
|
|
τ0mc |
|
f0mc |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
46
Углы α и β характеризуют положение взаимного углового энергетического спектра рассеянных волн основной и кросс-поляризации. Вследствие слабой зависимости результата от этих углов в пределах небольших их изменений в качестве α и β может использоваться направление прихода регулярной составляющей любой поляризации. Так же, как и (12), выражение (13) справедливо для любых α и β, кроме малых участков углов вблизи α = 90о и β
=90о.
9.Фазовые расстройки между регулярными и случайными составляющими для каждой
поляризации γm ( r ) = ϕmreg ( r ) −αεm ( r );γc ( r ) = ϕcreg ( r ) −αεc ( r ) . |
(14) |
Фазовая расстройка для каждого компонента может быть выражена через угловые расстройки δαm,c и δβm,c , представляющие собой разность между углами прихода регулярных составляющих и средними углами прихода случайных составляющих. Считая, что ширина угловых спектров случайных составляющих в обеих плоскостях невелика, можно полагать, что средние углы прихода этих составляющих связаны с величинами αεm,c соотношениями типа (10). Принимаем также
sinδαm,c ≈ δαm,c ; sin δβm,c ≈ δβm,c ; cos δαm,c ≈ cos δβm,c ≈ 1.
При этих предположениях получим:
|
|
G |
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
γ |
|
( r ) ≈ |
|
|
x(δα |
|
cosα cosβ |
|
−δβ |
|
sinα |
|
sin β +δα |
|
δβ cosα |
|
cosβ ) − |
||||||||||||||||||||
|
λ |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
m,c |
|
|
|
|
|
m,c |
|
|
m,c |
|
|
|
|
m,c |
|
|
|
m,c |
|
|
|
|
m,c |
|
m,c |
|
m,c m,c |
|
m,c |
|
m,c |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
− |
2π |
|
y(δα sinα |
|
cosβ |
|
+δβ |
cosα |
|
|
sin β |
+δα |
δβ |
sinα |
sin β |
|
) + |
||||||||||||||||||
|
|
λ |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
m,c |
|
|
m,c |
|
m,c |
|
|
|
|
m,c |
|
|
|
|
m,c |
|
|
m,c |
|
m,c m,c |
m,c |
m,c |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
2π |
|
zδβ |
|
|
cosβ . |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m,c |
|
|
m,c |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Здесь δαm,c |
= αm,c − |
|
;δβm,c |
= βm,c − |
|
|
. В случае βm,c = (βm,c )ran = 0 |
|
|
|
|
||||||||||||||||||||||||||
(αm,c )ran |
(βm,c )ran |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
rG) ≈ |
2π |
|
|
|
|
|
x cosαm,c − |
y sinαm,c ) . |
|
|
|
|
(15) |
||||||||||||
|
|
|
|
|
|
|
|
|
γm,c ( |
|
δαm,c |
( |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|||||||||||||||||||||||
10. Фазовая расстройка между разностью фаз регулярных составляющих основной и |
|||||||||||||||||||||||||||||||||||||
кросс-поляризации и фазой взаимной корреляционной функции обоих сигналов |
|
|
|
||||||||||||||||||||||||||||||||||
|
γmc ( rG) = ϕmc ( |
rG) +ψ −αεmc ( |
rG) = |
|
|
ϕmc ( |
|
rG) +ψ −[αεm ( rG) +αεmc (0)] |
= |
|
(16) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= γm ( |
rG) +ψ −αεmc (0), |
|
|
|
|
|
|
|
|
||||||||||||||||
где αεmc (0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
представляет собой фазу взаимной корреляционной функции при совпадающих |
|||||||||||||||||||||||||||||||||||||
значениях аргументов (в отличие от автокорреляционной функции, она может не быть равной нулю). Для стационарно связанных процессов величина αεmc (0) не зависит от r , что
фактически означает совпадение средних углов прихода случайных составляющих основной и кросс-поляризации. В этом случае
|
δαc = αc −αm +δαm ;δβc = βc − βm +δβm . |
(17) |
|
Все параметры, характеризующие нормальную (гауссову) модель векторного поля, |
|||
перечислены в табл. 1. |
Таблица 1 |
||
|
Параметры нормальной модели векторного поля |
||
|
|
|
|
Обозначение |
Наименование |
|
|
P |
Общая мощность поля основной поляризации |
|
|
g |
Параметр когерентности поля основной поляризации |
|
|
αm |
Угол прихода регулярной составляющей сигнала основной поляризации в |
|
|
|
горизонтальной плоскости |
|
|
ξ |
Модуль поляризационного коэффициента - отношение амплитуд регулярных |
|
|
|
составляющих сигналов кросс- и основной поляризации |
|
|
αc |
Угол прихода регулярной составляющей сигнала кросс-поляризации в горизонтальной |
|
|
|
плоскости |
|
|
ψ |
Фаза поляризационного коэффициента - разность фаз регулярных составляющих |
|
|
47
|
сигналов основной и кросс-поляризации при совпадающих значениях аргументов |
d0m |
Поперечный горизонтальный пространственный радиус огибающей функции |
|
корреляции сигнала основной поляризации на уровне 1/e |
d0c |
То же для сигнала кросс-поляризации |
d0mc |
То же функции взаимной корреляции сигналов основной и кросс-поляризации |
|
(половина ширины взаимной корреляционной функции) |
δx |
Смещение максимума поперечной взаимной корреляционной функции сигналов |
|
основной и кросс-поляризации |
η |
Отношение средних квадратических отклонений сигналов кросс- и основной |
|
поляризации |
δαm |
Угловая расстройка регулярной и случайной составляющих сигнала основной |
|
поляризации в горизонтальной плоскости |
f0m |
Радиус частотной корреляции сигнала основной поляризации на уровне 1/e |
f0c |
То же сигнала кросс-поляризации |
f0mc |
То же функции взаимной корреляции сигналов основной и кросс-поляризации |
|
(половина ширины взаимной корреляционной функции) |
τ0m |
Радиус временной корреляции сигнала основной поляризации на уровне 1/e |
τ0c |
То же сигнала кросс-поляризации |
τ0mc |
То же функции взаимной корреляции сигналов основной и кросс-поляризации |
|
(половина ширины взаимной корреляционной функции) |
βm |
Угол прихода регулярной составляющей сигнала основной поляризации в |
|
вертикальной плоскости |
βc |
То же сигнала кросс-поляризации |
z0m |
Высотный пространственный радиус огибающей функции корреляции сигнала |
|
основной поляризации на уровне 1/e |
z0c |
То же сигнала кросс-поляризации |
z0mc |
То же функции взаимной корреляции сигналов основной и кросс-поляризации |
|
(половина ширины взаимной корреляционной функции) |
δz |
Смещение максимума высотной взаимной корреляционной функции сигналов |
|
основной и кросс-поляризации |
δβm |
Угловая расстройка регулярной и случайной составляющих сигнала основной |
|
поляризации в вертикальной плоскости |
Rmax |
Произведение максимальных значений коэффициентов корреляции сигналов основной |
|
и кросс-поляризации по различным аргументам |
При отсутствии данных о различии ряда параметров сигналов основной и кроссполяризации приходится предполагать, что
αm = αc = α ; βm = βc = β ; d 0 m = d 0 c = d 0 m c = d 0 ; z0 m = z 0 c = z 0 m c = z 0 ;
δx = δz = 0; f 0 m = f 0 c = f 0 m c = f 0 ; τ0 m = τ0 c = τ0 m c = τ0 .
Можно также допустить ψ = 0, Rmax = 1, хотя это наименее оправдано. При указанных предположениях количество параметров для характеристики векторного поля сокращается до 12, от случая скалярного поля этот набор отличается тем, что используются дополнительные величины ξ и η.
Для определения параметров модели поля могут проводиться специальные экспериментальные исследования. Однако, большинство перечисленных параметров в процессе экспериментов непосредственно не измеряется. Чаще всего опытным путем исследуются огибающая и фаза (разность фаз) принятых сигналов или их различные нелинейные функции. Аналитически связать статистические характеристики этих функций с параметрами модели трудно, это проделано лишь для некоторых частных случаев. Например, двумерная плотность вероятности амплитуды и фазы [3]
W(E1 , E2 ,ϕ1 ,ϕ2 ,r , r ) = W0 AB, |
(18) |
где W0 - распределение W при отсутствии регулярной составляющей поля, A - постоянный сомножитель, зависящий только от регулярной составляющей и элементов ковариантной матрицы, B - сомножитель, определяемый, в основном, фазовыми соотношениями регулярной и случайной составляющих:
48
|
W = |
|
|
|
V1V2 |
|
|
|
exp − |
|
1 |
|
|
V 2 +V 2 − 2 f |
V V |
cos(ϕ |
1 |
−ϕ |
2 |
−α |
ε |
) |
; |
||||||||||||||
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
0 |
|
2π |
σ |
) |
|
|
|
|
|
|
|
2 [ |
1 |
2 |
|
ε |
1 2 |
|
|
|
|
|
|
] |
||||||||||||
|
|
|
|
|
(1 − fε |
|
|
|
|
|
|
1 − fε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2g |
2 |
|
|
1 −b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
A = exp − |
|
|
|
|
cos( ϕ |
|
|
−α |
|
) ; |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
1 − fε2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ |
ε |
|
reg |
|
ε |
] |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
B = exp{ |
|
2g2 |
|
[V1 cos(ϕ1 −ϕreg1 ) +V2 cos(ϕ2 |
−ϕreg2 ) − |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 − fε |
|
|
|
|
|
|
|
|
|
|
|
|
+ϕreg1 −αε )]}. |
|
|
|
|
|
|||||||||
|
|
|
|
|
− fεV1 cos(ϕ1 +ϕreg2 |
−αε ) − fεV2 cos(ϕ2 |
|
|
|
|
|
|
|||||||||||||||||||||||||
(rG,rG |
Здесь индексами 1 и 2 обозначены значения переменных при двух значениях аргумента |
||||||||||||||||||||||||||||||||||||
+ rG); V |
= E |
1 |
/ (σ |
2 );V |
2 |
= E |
2 |
|
/ (σ |
|
2 ) ; |
остальные |
|
обозначения те |
же, |
что и ранее. |
|||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Принято также, что поле стационарно, регулярная составляющая представляет собой плоскую немодулированную волну, так что
Ereg (r ) = Ereg (r + r ) = Ereg ; ϕreg ( r ) = ϕreg (r ) −ϕreg (r + r ).
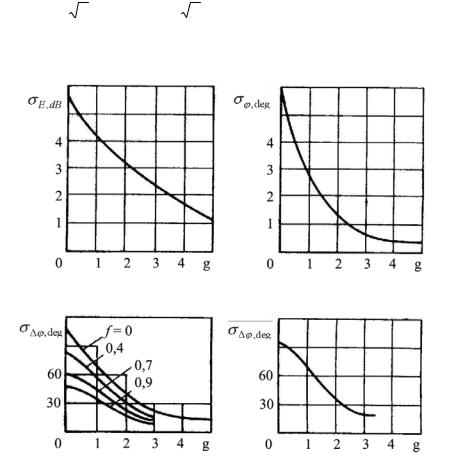
Рис. 1. Параметр когерентности и среднее квадратическое отклонение флуктуаций амплитуды, фазы, разности фаз и средняя разность фаз при равновероятном значении фазовой расстройки
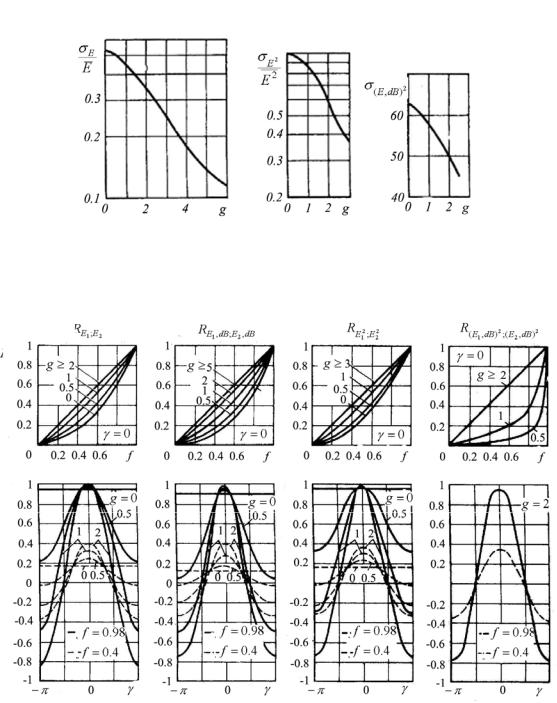
Зная распределение (18), не представляет принципиальных трудностей записать общие формулы для ковариантных функций амплитуды, фазы и любых их преобразований. Однако, попытки вычислить интегралы часто остаются безуспешными, а в случае, когда такое вычисление оказывается возможным, результаты обычно чрезвычайно громоздки и еще менее наглядны, чем исходные интегральные соотношения. Поэтому на рис. 1-5 приведены некоторые важные для практики результаты вычислений статистических характеристик, проведенных на ЭВМ методом статистических испытаний. Буквами σ и R обозначены соответственно среднее квадратическое отклонение и нормированный коэффициент корреляции для величин, указанных в индексе. Через E,dB обозначена амплитуда, выраженная в децибелах (например, величина сигнала на выходе логарифмического приемника); ϕ = ϕ1 - ϕ2. Интервал однозначности фазовых измерений принят равным ±π.
49
При другом интервале однозначности масштаб фазы (разности фаз) должен быть соответственно изменен.
Обращает на себя внимание сильная зависимость характеристик поля от фазовой расстройки или фазы корреляционной функции αε, что имеет место при несимметричных спектрах сигналов. Опытные данные [2,4] подтверждают необходимость учета несимметрии спектров при анализе структуры реального электромагнитного поля, особенно на закрытых и полуоткрытых трассах с рассеянием. Наиболее типичны небольшие изменения положения углового спектра рассеянных сигналов относительно угла прихода регулярной составляющей, что при разнесении приемных антенн (или элементов одной антенны), значительно превышающем длину волны, приводит к большим значениям γ даже тогда, когда цель или источник излучения находится на равносигнальном направлении.
Рис. 2. Зависимость флуктуаций амплитуды сигнала и ее нелинейных функций от соотношения регулярной и случайной составляющих
Рис. 3. Коэффициенты корреляции уровня сигнала при разнесенном приеме
50
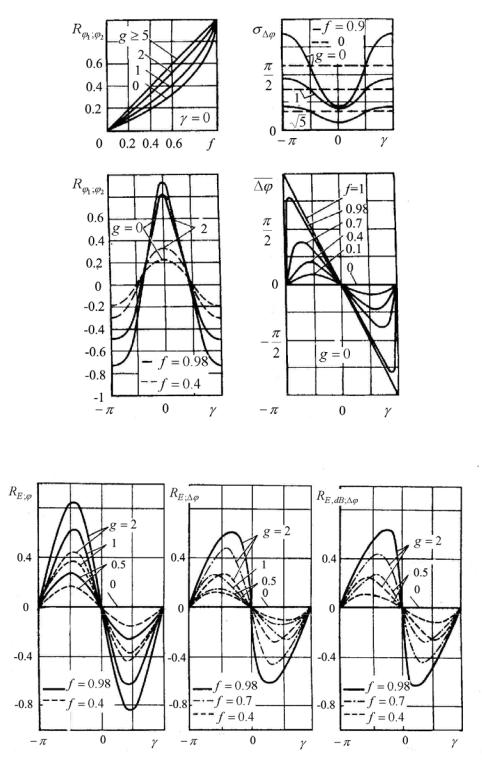
Рис. 4. Статистические характеристики фазы и разности фаз при разнесенном приеме
Рис. 5 . Коэффициенты корреляции параметров амплитуды и фазы поля с несимметричным спектром
Приведенные соотношения и графики могут быть использованы для восстановления (определения) параметров нормальной модели по опытным данным. Вначале целесообразно определить параметр g по одной из кривых на рис. 1 или 2, затем, при совместном использовании двух других измеренных характеристик, найти f и γ. Наличие большого числа одновременно измеренных параметров сигналов может быть использовано для проверки справедливости нормальной модели.
