Практикум 5 (Численные методы) - Решение уравнений вида f(x) = 0
.pdf
|
|
|
|
|
|
Практикум5 |
.Решенуравненийвида |
|
f(x) = 0. |
|
|
|
||||||||
|
|
|
|
Методы деления отрезка пополам,Ньютона,простыхитераций |
|
|
|
. |
|
|
|
|||||||||
|
Рассмотримзадачу |
|
нахождкорнейфункцииоднойнияпеременной |
|
|
|
, т.е.решениянел |
и- |
||||||||||||
нейногоуравнениявида |
|
|
|
|
|
|
. Численрешениедауравненныхое |
|
разбиваетсяндвао |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
ийобыч ( ) |
|
|
|
|
|
|||||
этапа: |
|
|
|
|
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
1)Локализациякорней |
|
– выделотр,накотезкниенаходитсярыхвнебодноголеекорня. |
|
|
|
|
|
|
|
|
|||||||||
Обычноосуществляетиспользуялибографически,либоаналитичзвсвойстваесфункитные |
|
|
|
|
|
|
|
|
|
|
|
к- |
||||||||
ции.Еслилокализацияпроведеневер,т нао |
|
|
|
|
|
|
|
.е.наотрезкеостабодноголееоськорня,топослед |
|
|
|
|
|
|
|
у- |
||||
ющиеметонеработатьгутдыилиработатьнестабильно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2)Поисккорфункциинаотрезкеясзаданточ.Методыно,которыейстьюприэтомспол |
|
|
|
|
|
|
|
|
|
|
ь- |
||||||||
зуют,мырасдалееясмотримвтекущейработе. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1. Методделени |
|
я отрезка пополам. |
|
|
|
|
|
|
|
|
|||||||||
|
Первыйметод,которыймырассмотрим,это |
|
|
|
|
методделения |
|
отрезка пополам (влитературе |
||||||||||||
егоещеназывают |
|
|
|
методомбисекции |
|
,либо |
методомдихотомии |
). |
|
|
|
|
|
|
|
|||||
|
Пустьнаконцахотрезка |
наэтомотрлежитзке[ !, !] |
функция значенияфункцииимеютразличныезнаки,т.. |
|
= 0 |
|
|
|||||||||||||
! ! |
< 0 |
.Тогда |
|
хотябыодинкорень |
|
уравнения |
.Найдемс |
е- |
||||||||||||
отрезка |
|
|
! = ( ! + !)/2 |
ивычислимзначениефункцииэтойчке |
|
( !) |
.Издвухполовин |
|
||||||||||||
рединуотрезка |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
изкорлежитн [ !, !] |
и |
[ !, !] |
выберемту,наконцахкоторойфункцияимеетраззнаки, какыеодин |
|
|
|
|
|
|
|
з- |
|||||||||
|
этойаейполовине.Затемновыйотрдепополаммзокивыбиполовинусраем |
|
|
|
|
|
|
|
|
|
|
|
||||||||
личзнакамифункцииымиконц,такдалее. х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ,где |
|||||
|
Будемпродолжатьделтотехпорние,покадлин |
|
|
|
|
|
а новогоотрбудетпревышатьзка |
|
|
|
|
|||||||||
– требуемаяточность. |
|
|
|
|
Тогдасерединапоследнегоотрезкадастприближенноезначекорняс ие |
|
|
|
|
|
|
|||||||||
требуемойточностью |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
= 0 |
|
|||
|
Пример 1. Наподпрограммуисать |
|
|
-функциюдлянахождениякоуравненияня |
|
|
|
|
|
|
||||||||||
отрезке |
[ , ] |
спомощьюетделенияотрезкадапополам |
|
|
|
. |
|
|
|
|
|
на |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
function [x,n]=bisection(f,a,b,eps) |
|
|
|
|
|
|
|
|
||||||||||
|
|
n = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
while (b-a)>2*eps |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
x = (a+b)/2; |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
if (f(a)*f(x) < 0) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
b = x; |
|
|
|
%Выбиотраемезок |
[a,x] |
|
|
|
|
|||||
|
|
|
|
|
|
else |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = x; |
|
|
|
%Выбиотр[аемезок |
x,b] |
|
|
|
|
|||||
end
n = n+1;
end
x = (a+b)/2;
end
Пример 1 (продолжение). Спомощьюнаписаннфункцвычкореньиуравненияслитьй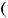 
− 0.2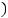
= 0 наотрезке [0, 1] сточностью = 10!!.
>>a = 0;
>>b = 1;
>> f = @(x)(x-0.2); |
%Задаемфункциюввидеуказателя |
>>eps = 1e-3;
>>x = bisection(f,a,b,eps)
x =
0.2002
лю): |
|
Дляпроверкинайдем |
значениефункциив |
|
|
|
полученнойточкеоно(д бытьлжноблизким |
|
|
у- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
>> f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ans = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.9531e-04 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Упражнение 1. Длявыполненияупр |
|
|
ажнениявыбратьуравнение |
|
|
всоответствииномером |
|
||||||||
компьютерасписок( вариантовприведенконцеработы). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1)Спомощьюграфифунопределитькацииоблокализацииастикорнейуравнения |
|
|
|
|
|
|
|
|
|
|
|
|
, тоесть |
||
определить начальныеотрезки |
,со держащиеодинвнокорфу,нкцииь |
|
|
|
|
|
дляпримененияметода |
е- |
|||||||||
ленияотрезкапополам |
(длинуотрезковвыбирайте |
|
|
|
|
вдиапазонеот0до.21 |
|
). |
|
|
|||||||
стью |
|
2)Спомощьюетделенияотрезкадапополамнайтивсекорнизаданнуравнесточнгоия |
|
|
|
|
|
|
|
|
|
|
|
|
о- |
||
= |
10!4. |
|
|
|
|
|
|
|
!! |
|
!! |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3)Дляодногоизк |
орнейопределитьчитесло, ацийебуемыхдлянахождзначения |
|
|
|
|
|
|
||||||||
корняпри |
|
четырех значенияхточности |
: |
.10 |
!! |
, 10 |
!! |
, 10 |
, 10 |
(начальныйотрезок |
необходимо вы- |
||||||
биратьодиндлякаждогоковымрасчета) |
|
|
|
|
|
|
|
|
|
|
|||||||
2. Метпростыхитерацийд.
|
Заменим уравнение |
= 0 |
эквивалентнымемууравнением |
|
|
|
|
|
|
.Этом сделатьжно |
|
|
|
||||||||||||||||||
различнымиспособами,на, римероложив |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– некотораязнакопост |
|
|
о- |
|||||||||||
|
|
|
|
|
|
|
= + ( ) |
,где = ( ) |
|
|
|
|
|
|
|
||||||||||||||||
яннаяфункция. |
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Выберемнекотоначальноеприближение |
|
|
!!! = ! |
! |
ивычипослприближенедующиеим |
|
|
|
|
|
|
|
|
ияр |
е- |
|||||||||||||||
куррентнопоформуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Еслипртакомпостроенииполученнаяпоследовательприбудетлижиметьпр делнийость |
, = 0,1,2, … |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
тозначеданногопределаие |
|
|
|
|
исходногоуравнения. !→! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
будетявлятьсякорнем |
|
|
|
= lim , |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Данныйметодполучилназвание |
|
|
|
метпритерацийостыхд |
|
|
|
. Условиемсходиданногоости |
|
|
|
|
|
|
||||||||||||||||
методаявляетсяусловие |
|
ограниченпроизводнойфункциости |
|
|
! |
|
|
|
|
|
|
|
( ) вблизикорня |
|
: |
|
|
|
|
|
|
|
|||||||||
|
Чеммезначениеьше |
|
|
константы q |
|
|
|
≤ < 1. |
|
|
|
Начальноеприбл |
и- |
||||||||||||||||||
|
|
|
|
|
|
тембыстрееметсходккорню.ится |
|
|
|
||||||||||||||||||||||
жениетакжедолжнобытьвыбраносучетомданногоограничен,т..изусловия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
! |
< 1 |
. |
|
|
||||
|
Такимобразом,дляприменеобходтоданимостиоченьаккуратновыбиратьмоэквивален |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т- |
|||||||||
ноепредставлениеуравне..(функциюия |
|
|
|
! = |
|
|
|
|
|
|
)иначальноеприб |
лижение |
|
!). |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Например,дляуравнения |
|
|
|
|
можновыбратьпредставления |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
( ) |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
= |
или = |
|
+ |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
(легкопроверить,что |
|
|
|
|
|
|
! |
|
= |
||||||
|
Впервомслучаеметодпростыхитерациинесходится |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
длюбогоя |
),авовтором |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= !!!! |
|||||||
! ≠ 0 |
. |
> 2 |
|
|
|
– метсходится |
|
|
(причемдостаточнобыстро) |
|
|
|
прилюбомвыборе! |
|
|
!!! |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Практическим |
ритериемостановкиитерационногопроцесса |
|
|
|
|
|
|
|
|
|
|
|
|
вметодеявляетсяусловие: |
|
|
|
|
|
|
|
||||||||||
2
|
|
|
|
|
|
|
|
|
|
! − !!! = |
! − !!! ! |
|
< , |
|
|
|
|
||||||||||||
где |
|
|
|
|
условнгарантируеенииого,чторазносятсяь |
|
|
|
!!! |
|
|
! |
|
!!! |
|
|
|
|
|
|
|
||||||||
– некотораязаданточ.Принвыполаяостьдан |
|
− 1 |
|
|
|
|
|
2 |
− |
− |
|
|
|
|
|
|
|
|
|||||||||||
междузначенипослитерациеймднейискомымрнем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! − |
< |
. |
|
|
|
|||||||
|
Пример 2На. подпрограммуисать |
|
|
|
|
-функциюдлянахождениякоуравненияня |
|
|
= ( ) |
сп о- |
|||||||||||||||||||
мощьюмет |
одапростыхитераций. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
function [r,n] = simple_iterations(g,x0,eps) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
x=[x0 g(x0) g(g(x0))]; |
|
|
%Пердвеитерацииыевыполняемотдельно |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
n = 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
while ((x(end)-x(end-1))^2)/abs(2*x(end-1)-x(end)-x(end-2)) > eps |
|
||||||||||||||||||||||||||
|
|
|
x = [x g(x(end))]; |
|
|
%Вычисляемзначениеновойитерации |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
n = n+1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
if (n > 1000) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
disp('n > 1000'); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
break; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
end |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
end |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r = x(end); |
|
|
|
|
|
|
%Вкачествекорнявыбирапослзначениемднее |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
end |
|
|
|
|
|
|
|
|
− 1 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
||
|
Упражнение 2. |
|
,б) |
|
! |
|
|
,в) |
|
|
|
|
|
|
,г) |
|
|
|
|
|
|
||||||||
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|||||||||
|
Для решенияура |
|
внения |
|
|
|
! |
|
предложеноварианта4 представлениявиде |
|
|
|
|
! |
|
! |
|||||||||||||
|
|
|
|
= |
! |
|
= + |
− 1 |
|
= − |
! |
|
! |
− 1 |
|
|
= |
+ |
|
||||||||||
|
Для каждогоиз |
|
|
|
|
! |
|
|
|
! |
! |
|
|||||||||||||||||
|
|
заданныхпредставлений: ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1)Найтиобластьсходимитерацийметодапростна(бумаых |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
геилив |
Matlab). |
|
||||||||
|
2)Вычислитьзначекорнуравненияие(слийэтозможно)длячетырехзначенийначал |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
ь- |
||||||||||
ногоприближения: |
= −1.5, = −0.5, = 0.5, = 1.5 |
сточностью |
10!4. |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Примечание: |
Если начальноеприбл |
|
|
ижениенаходитсягранилзапределамице |
|
|
|
|
|
|
области |
|||||||||||||||||
сходимости,найденнвп. расходимо1, методайтакженадопрспомощьюветьрасчетаить. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дляданного |
|||||||
|
3)Наосновепроведенныхрасчетовопределитьнаилучшийвыборфункции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. МетодНьютона
Рассмотримуравнение |
= 0 |
.Пустьдляфунк |
|
|
ции |
|
известнапроизводная |
′( ) |
(либо |
|
еезначеможнолегкоиеайтивпроизвольнойточке |
|
|
|
). |
Выберемнекотоначальноеприближение |
|
||||
|
|
! |
|
( ) |
|
|
||||
! вблизикоуравненияня |
ип остроимитерацпроцессви: онныйда |
|
|
|
|
|
|
|||
|
!!! = ! − |
! |
! |
, = 0,1,2, … |
|
|
|
|||
Такойитерационныйпроцессявляечаслучаемнымсяметодапростыхитераций |
|
||
выборэквивалентногоураявляетсяненопт мальным |
|
|
|
название методНьютона |
. |
|
|
ГеометрическийсмыслметодаНью |
|
|
|
сяпоабсциссамточекпересеченияасательныхкграфикуданнойфункции,провто,чкахдимых |
|
||
соответствующихпредыдущимприблсм(. нижесунокжениям)Отсюда. появилвторназвосье |
|
||
ниеэтогометода |
– методкасательных |
. |
|
. Приэтом
( !: !
!
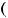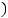= 0).Данныйметодполучил
тонаследующ:приблккорнюиженией |
осуществляет- |
а-
|
Пракртокончанияскимитериеитераципроцедляоснногозадантижесато нияой |
|
|
|
|
ч- |
|
ности являетсяусловие: |
! − !!! |
< , |
|
|
|||
|
Следуетиметьввиду,чтоскорсхометодадимоссильстьНьюзависитоотнаочальн |
|
о- |
||||
приближения иприплохвыборет мчки |
! |
методможетсхоченьдитмедленно. ся |
|
|
|||
го |
Еслифункциямонотвнекоторойокрестннакор, д яости |
|
лявыборахорошегоначальн |
ого |
|||
приближения можно использовать следующееправило |
|
: |
|
|
|||
|
Теорема. |
Пустьзадафунакция |
( ) иопредел |
енитерационныйпроцесс |
Ньютона |
|
|
|
|
!!! = ! − |
! |
, = 0,1,2, … |
|
|
|
|
|
! ! |
|
|
|||
|
Есдвсехлия |
[ , ] справедливоодноизследующихусл: вий |
|
|
|
||
1)'
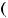
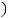> 0, ''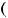
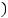> 0, ! = ,
2)'
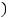< 0, ''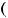
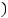< 0, ! = ,
3)'
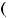
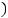> 0, ''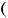
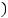< 0, ! = ,
4)'
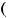
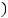< 0, ''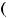
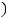> 0, ! = ,
|
. |
|
! |
– монотсходитсякточкенно |
|
,являющкорнуравнемйся |
|
ения |
тогдапоследовательность |
|
|
|
|||||
= 0 |
|
|
|
|
|
|
= 0 |
|
Пример 3На. подпрограммуисать |
-функциюдлянахождениякоуравненияня |
|
сп о- |
|||||
мощьюметода |
|
Ньютона. |
|
|
|
|
||
function [x,n] = newton(f,df,x0,eps) n = 0;
while (1)
x = x0 - f(x0)/df(x0); n = n+1;
if abs(x-x0) < eps break;
end
4
x0 = x; |
|
|
|
|
|
|
|
|
|
|
|
end |
|
|
|
|
|
|
|
|
|
|
|
end |
|
|
|
|
|
|
|
|
|
|
|
Упражнение 3. Длявыполне |
|
упражнениявыбратьурав |
|
|
нение всоответствииномером |
|
|
||||
компьютерасписок( вариантовприведенконцеработы). |
|
|
|
|
|
|
|
|
|
|
|
1) Дляотрезлокализациикоуравнениярней,найденныхвупражнении1, |
|
|
|
|
|
выбратьоднуиз |
|
|
|||
граничточеквкачественачальногоыхприближенияметодаНьютона(основезнаков |
|
|
|
|
|
|
|
производ- |
|
||
ных). |
|
|
|
|
|
|
|
|
|
|
|
Примечание: |
Есликорнейнесколько,тоначальноеприближопределдлякаждогониеть |
|
|
|
|
= |
|
|
|||
корня. |
|
|
|
|
|
|
|
|
10!4 |
|
|
2) СпомощьюетодаНьютнайтивсекорнизаданннауравнесточностьюгоия |
|
|
|
|
|
, |
|||||
исптоначальногользуячкиприближениявыбрапункте1.ные |
|
|
!! |
!! |
!! |
|
!! (начальноеприближениевыбирать |
|
|
||
3)Дляоднизкоопределитьрнейгочитесло, ацийебуемыхдлянахождзначения |
|
|
|
|
|||||||
корняпричетырехзначенияхточности: |
|
|
|
|
|
|
|
||||
одинаковымприкаждомрасчете |
|
). |
Сравнить полученный результат с резупражненияльтатом1. |
|
|
|
|||||
|
|
10 |
, 10 |
, 10 |
, 10 |
|
|
|
|
||
Примечание: Впункте3 |
необходимо исследовать корень,совпадающийкорнемиз |
соответ- |
|
||||||||
ствующего пунктаупражнени |
я 1. |
|
|
|
|
|
|
|
|
|
|
4. Решениеуравненияспомощьювстроен |
|
|
ныхфункций |
MATLAB |
|
|
||
В MATLAB длярешенуравненийвидая |
|
|
предназначена функция fzero,вкачестве |
|
||||
парамкотоертроведаетсяой |
указательнафункцию |
иначальноеприближениекорняили(отрезок |
|
|
|
|||
= 0 |
|
|
|
|
||||
егос держ)Обратите. внимание,щийчто |
|
fzero такжекаки |
|
методдихотомиитребует,чтобыпри |
|
|
||
перчкореходерезфуменкцияьзннапри(ялаак,сеепомнудастсяеощьюрнайтинулифун |
|
|
|
|
|
|
к- |
|
ции, f(x)=sin(x)+1,корниполиномадвойнойкрат..)ности |
|
|
|
|
|
|
|
|
Подробописаниефупроекциииспользованиямерамиможнопосмотр |
|
|
|
|
етьвсправке |
|
||
MATLAB,набрав |
doc fzero. |
|
|
|
|
|
|
|
Упражнение 4. |
|
|
|
|
|
|
|
|
Длявыполненияупражнениявыбратьуравнесоответствииномеромиякомпьютерасп( |
|
|
|
|
fzero найтивсекор |
|
и- |
|
соквариантовприведенконцеработы)С.помощьювстроеннойфункции |
|
|
|
|
низ |
а- |
||
данногоуравнения.Начал |
ьныеприближения |
|
выбрать те же, что и в упражнениях 1и 3. Сравнитьп |
о- |
||||
лученныйрезультат. |
|
|
|
|
|
|
|
|
Задлявыполненияаниялабораторнойработы.
Номервариантасоответствукомпьютерапоследнцифреномера.й
№ |
f(x)=0 |
|
вар |
||
|
||
1 |
cos − + 1 = 0 |
|
3 |
1 |
|
5 |
sin − 2 + 2 = 0 |
|
|
− sin ! − 1 = 0 |
|
7 |
! − !! = 0 |
№ |
|
|
f(x)=0 |
вар |
|
|
|
|
|
|
|
2 |
|
! − 4 = 0 |
|
4 |
! − 3 + 2 = 0 |
||
6 |
! − ! − 9 + 9 = 0 |
||
8 |
sin |
3 ! |
|
|
2 − 2 + 1 = 0 |
||
9 |
1 − |
! |
+ |
1 |
|
! |
= 0 |
0 |
− 1 |
! |
− |
1 |
|
! |
= 0 |
|
|
6 |
|
|
|
2 |
|
6