Практикум 2 (Численные методы) - Интерполяция функций
.pdf
|
|
|
|
Практикум2 |
. Интерполяцияфункций |
. |
|
|
|||
|
|
|
|
Кусочно-линейнаяинтерполяция |
. |
|
|
|
|||
|
|
|
ИнтерпмногочлеЛаграНьютонажаляционые |
|
|
|
|
. |
|
||
Пуданасеткатьузлов |
! = !, !, … , ! |
,где |
. ! < ! |
< ! < < ! |
,иизвестнызначения |
|
|||||
функции |
|
вузлахсетки: |
|
|
|
||||||
|
|
! = ! , = 0,1, … , |
Требуетсянайтизначениефункции |
|
для |
||||||
некоторого |
|
|
несовпадающегоузламисетк. |
|
|
|
|
|
|
|
|
Задача нахождениятакого!значения! |
функции получиланазадачивание |
|
|
терполяции. |
|
||||||
|
|
|
, |
|
|
|
|
||||
1. Кусочно-линейнаяинтерполяция
Наибпростымспособомлееинтерполяцииявляет |
|
|
|
|
название – линейнаяинтерполяция) |
:искомаяфункция |
|||
функцсоединяющей) звестныезначенияфункции.Полученнуютакимобразомфункциюможно |
|
|
|
|
описуравнениемть |
(длякаждого |
трезка) |
: |
|
|
|
! − !!! |
||
|
|
= !!! + |
! − !!! |
|
ся кусочно-линейнаяинтерполяция |
(другое |
заменяетсяломанкусочно( й |
-линейной |
− !!!
, 
!!!, !
.
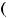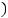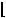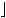Дляпогрешнформулыкусочности |
|
|
|
|
-линейнойинтерполяции |
|
|
|
справоц:енкадлива |
|
|||||||
|
|
|
|
≤ ! max!!!!,!! |
!! |
! − !!! ! |
. |
|
|
|
|||||||
Такспинтерполяциийсобобычноиспользуетсявтехслучаях,когданетребуетсявысокая |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
||||
точностьпредставленияфункции.Напр, мер |
|
|
|
|
|
MATLABпользуетсякусочно |
|
|
|
|
|
-линейнойинтерполяц |
и- |
||||
ейприпостроенииграфикапомощьюфункции |
|
|
|
|
|
|
plot (придостаточномчислевходных |
|
точекизл |
о- |
|||||||
манностькривойна становиункепракнезаметнойическиься). |
|
|
|
|
|
|
|
|
! сшагом |
|
|
|
|||||
Пример 1. Приборвыдаетсигналпозакону |
|
|
|
. |
|
|
|
|
.Наблюдательзафи |
к- |
|||||||
найтизначесигвточкениеала |
|
|
|
|
= 0, 0.5, 1, 1.5, 2 |
|
Используялинейнуюинтерполяцию |
|
|||||||||
сировалпять |
отсчетов функции |
вточках |
|
|
= . |
|
|||||||||||
|
|
|
|
|
|
|
= 0.5 |
|
|
||||||||
|
>> x=0:0.5:2; |
% |
= 0.75 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
исходданные |
|
|
|
|
|
|
|
|
|
|
|
||||
|
>> y=x.^2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0.2500 |
|
|
1.0000 |
2.2500 |
4.0000 |
|
|
|
|
|
|||||
|
>> t=0.75; |
|
%исследуемаяточкавкоторойищемзначесигниеала |
|
|
|
|
|
|
|
|
|
|||||
|
%Определяемотрезокзначение( |
|
|
|
|
|
i), соответствисследточкуеющиймо |
|
|
|
|
|
|||||
>>i=find(t<x,1,'first')
i =
3 %Строиминтерполяциюдлянайденногоотрезка
>>f=y(i-1)+(y(i)-y(i-1))/(x(i)-x(i-1))*(t-x(i-1))
f =
0.6250
>> err=f-t^2 %Ошинтерполяциибка err =
0.0625
Упражнение1 . Пуестьприбор,которыйвдискретмомевременивыдаетыесигналтыпо
закону 
= sin
.Допустим,наблюдательзарегистрирпяо счетвмоментывремениовал
! = !! , = 0,1, … 4.
1) Используялинейинтерполяциюнайдите, уюзначенияфункции |
,определитепогрешность |
вто |
чках |
= 0, |
! |
, ! |
, ! |
||||
|
|
|
! |
! |
! |
||||||
исравнитереальным |
значенсинусавэточкахем |
|
интерполяциив |
|
|
|
|
|
|
||
этихочках |
. |
|
|
|
|
|
|
|
|
|
|
2) Постройтеграфикисинуса |
|
(используяфункцию |
MATLAB fplot) иломаной,проходящей |
|
|
|
|||||
черезпятьзаданныхточек |
|
! (можновоспользов |
атьсяфункцией |
plot).Отметьте,насильноколько |
|
|
|
|
|||
ониразливразныхчаграфикастяхются.Чемэтообусловлено? |
|
|
|
|
|||||||
3)Постройтеграфик |
|
погрешности интерполяцисходнразность( междукривполой |
|
|
|
|
|
|
у- |
||
ченнойломаной)Определ. пографвкакойточкеиточкахку(те) |
|
|
|
достигаетсямаксимум |
|
погрешности |
|||||
иегопримерноезначение. |
|
|
|
|
|
|
|
|
|
|
|
4) Повторитеэкспусловииеримент,чторегистсигнпраоисходитловциядварчащеза ( ! = !! , = 0,1, … 8)Какизменится. погрешностьвычисленфункц? иия
2. ИнтерпмногочлеЛагранжаляцио ный
|
|
Построиммногочлминимальнойст,екоторыйпенивзаданныхузлах |
|
|
|
|
|
|
|
|
|
. ! = |
!, !, … , ! |
, |
|||||||||
! < ! < ! < < ! |
принимаетзаданныезначения |
|
|
|
! |
= ! |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
, = 0,1, … , n. |
|
|
е- |
|
||||||||||
пеньданмногодолжнабытьчлеединнижечаузсцу,т.ле.равнаов |
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно,чтост |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Лагранжпоказ,чтоук заннымл |
|
|
|
|
|
|
|
выше свойствобладаетмн: гочленм |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
! |
! |
!, |
|
|
|
|
|
|
|
||
|
|
|
|
! |
|
|
|
|
− ! |
|
= !!! !! |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
− ! |
− !!! |
− !!! ( − !) |
|
|
|
|
|
||||||||
|
|
|
|
! |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
Полиномы |
|
|
! |
! |
! |
|
! |
! |
!!! |
! |
!!! |
! |
! |
|
|
|
|||||
|
|
!! ( ) |
,котпо − |
− |
− |
− |
( − ) |
|
|
n, под- |
|
||||||||||||
|
|
|
|
|
|
рыелучилиназвание |
|
|
|
фундаментальныеполиномыстепени |
|
|
|
||||||||||
чиняютсяусловию: |
|
|
|
|
|
! |
|
1, = !, |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Нетпроверитьудно,чтоизэтогоусловияследуетвыполнениетребуемогосвойства |
|
! |
|
= 0, = !, ≠ . |
|
|
|
|
|
|
|
||||||||||
= |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
! |
! |
Построенный!такимспособоммногочленполучилназвание |
|
|
|
|
|
|
|
|
|
интерпмноляционныйг |
очлен |
||||||||||
Лагранжа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Пример 2. |
Наподпрограммуисать |
|
|
-функцвычзначениесляющуюинтерполяцион |
|
|
|
|
ного |
||||||||||||
многочленаЛагранжавточках |
|
|
|
|
|
t позначефувузлахнкциииям( |
|
|
x, y): |
|
|
|
|
|
|
||||||||
|
|
function f=lagr(t,x,y) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
f=[]; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
for ti=t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
fi=0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
for i=1:length(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
%числительфундаментальногополинома |
|
|
|
|
|
l_i |
|
|
|
|
|
|
|
|||||||
|
|
|
w=ti-x; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
w(i)=1; |
|
|
|
%исключаеммножительдляиндекса |
|
|
|
i |
|
|
|
|
|
|
||||||
|
|
|
u=prod(w); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
% знаменатель фундаментальногополинома |
|
l_i |
|
|
|
|
|
|
|
|||||||||||
|
|
|
w=x(i)-x; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
w(i)=1; |
|
|
|
%исключаеммножительдляиндекса |
|
|
|
i |
|
|
|
|
|
|
||||||
u=u/prod(w);
fi=fi+y(i)*u;
end f=[f,fi];
end end
|
3. |
ИнтерпмногочлеНьютоналяциный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Пустьнаотрезке |
|
|
|
, задравномернаясеткаузлов |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
! = !, !, … , !| ! = + , = 0, … , ; = |
. |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Определение. |
Величина |
! = !!! − ! |
|
|
|
|
|
|
|
|
|
|
= !!! − ! |
называется |
|||||||||||||||||||||||||
конечразпервогонопорядкастьюйили(разн«шагостьювперед»). |
|
|
= ! + − ! |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
!!! |
|
! |
= ( -!) |
называетсяконечразвторогонопорядкастьюй |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
величина |
|||||||||||||||||
|
|
Величина |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
, + ≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
=В |
|
|
называетсяконечразпорядканостьюго |
|
|
|
|
|
|
|
|
|
|
|
|
|
m. |
|
|
|
|
|
|
|
|||||||||||||||||
|
! |
|
MATLAB! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
для вычислеконечразможноисыхяптейвстрользфункциоеннуювать |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
diff(y, p), котораявычимазначенийсляетсивконечразпорядкаостейых |
|
|
|
|
|
|
|
= |
|
|
|
= |
|
|
= |
|
|
|
|
|
|
p повходномумассиву |
|
|
|||||||||||||||||
значефункцииий |
|
|
|
y. |
|
|
|
|
|
|
|
|
|
|
!!!! |
!!! |
|
!!!! |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Введембезразмернуюпеременную |
|
|
|
|
|
|
|
|
– расстояниемеждуначалом |
|
, эта |
||||||||||||||||||||||||||||
отрезка a иточкой |
|
t, выраженноечисузсеткилдляов( |
|
|
|
|
|
! |
|
|
!!! |
!!!!! |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
величинабудетдробной). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точек, |
несовпадузламисеткющих |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
ИнтерпмноЛаграляциогочленный |
|
|
|
|
|
|
|
нжаможнозаписатьвальтернативнойформе: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
! ! |
+ |
|
|
! |
! |
+ − 1 |
|
! ! |
+ + − 1 |
− + 1 |
! ! |
, [0, ]. |
|
|||||||||||||||||||||||||
|
|
|
|
= |
+ 1! |
|
2! |
|
! |
|
|||||||||||||||||||||||||||||||
|
|
Такаяформазаписиинтерполяциомногочлеполучиланазваногоие |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перваяинтерполяц |
и- |
||||||||||||
оннаяформулаНьютона |
|
|
|
|
илиформулаинтерполирован« |
|
|
|
|
иявперед». |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
ПоаналогииспервойинтерполяциформулойНьютможзаписатьонной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вторуюинте |
р- |
|||||||||||
поляционнуюформулуНьютона |
|
|
|
|
|
|
|
(формулуинтерполирования« назад»): |
|
|
|
|
|
+ 1 + − 1 |
|
! |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 1 |
|
! |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
! |
! + |
= ! + |
1! |
!!! + |
|
|
2! |
|
!!! + + |
|
|
|
|
! |
|
|
|
|
! |
, |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
− ! |
= |
− |
= |
− ! |
, − , 0 . |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Мыполучилитри |
|
|
|
различныхпредоднтогоставленияляжеинтерполяционного! |
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
номаинтерполяционный( полиномЛагранжа |
|
|
|
|
|
|
|
|
|
|
|
двеформыинтерполяционного |
|
|
|
полинома Ньютона). |
|
||||||||||||||||||||||||
|
|
ИнтерполяционныйполиномвформеЛаграсодержитз жаачения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
строить |
|
вявномвиде |
, |
|||||||||||||
приэткоэффмприциенты |
|
|
|
y зависяттолькоотпараметровсетки |
|
|
|
|
|
|
|
|
|
|
.Этоудобно,когданадоп |
! = ! |
|
|
|
|
|||||||||||||||||||||
интерполяционныйполиномтойжес , ткедлядругофункции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
( !) |
|
|
|
|
|
n |
||||||||||
|
|
ИнтерполяционныйполиномвформеНьютонасодержитзначения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
неявночерез( коне |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ч- |
|||||||||||||||||
ныеразн)Од. онудобенстиако,когдадлятойжефункции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
необходимоувеличитьчисузло |
|
|
|
|
|
|
|
|||||||||||||
дляповышенточн.Вэтомслучаестик ясходзаписимнодостаточногочленайдоба |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
витьн |
е- |
||||||||||
сколькотакихжечленов,еслизапасеосталисьн испоузсеткил.ьзованными |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Крто,напрактикегомеобычноформулу |
|
|
|
|
|
|
|
|
|
|
|
Ньютона используютдляинтерполяциивточках |
|
|
|
|
|
|
x, |
||||||||||||||||||||
близкихконцамотрезка |
|
|
|
|
.Вэтомслучае |
|
|
q (или |
p длявторогоконцаотрезка) |
|
|
|
|
|
|
малоитребуетсян |
|
е- |
|||||||||||||||||||||||
большоечислочленоврядляостиануточжнойеияости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. ВтожевремямногфоЛрмчлен |
|
|
|
|
|
|
а- |
|||||||||||||||
гранжадает,какправ,наимаксимаблольшуюабсолютнуюпогрешностььнуюв |
|
|
|
очках,близких |
|
||
краямотрезка |
. |
|
|
|
|
|
|
Пример3 |
. Наподпрограммуисать |
-функциювычисляющуюзначение |
функции вточках |
t |
|||
(можетбытьзадаточекссивн) |
|
позначефувузлахнкциииям( |
x, y) припомощипервойинтерп |
о- |
|||
ляционнойформулыНьютона |
: |
|
|
|
|
|
|
function f=newton(t,x,y) |
|
|
|
|
|||
|
n=length(x)-1; |
%Нумерацияв |
MATLAB начинается1 |
|
|
||
|
f = []; |
|
|
|
|
|
|
|
for ti=t |
|
|
|
|
|
|
|
q=(ti-x(1))/(x(end)-x(1))*n; |
|
|
|
|||
|
fi=y(1); |
|
|
|
|
|
|
|
for i=1:n |
|
|
|
|
|
|
|
|
dy=diff(y,i); |
% Конечразнаяость |
i-гопорядка |
|
|
|
%Вычисляемпроизведение q(q-1)...(q-i+1) w=q-(0:(i-1));
u=prod(w);
%i-йэлементрядавформуле Ньютона
fi=fi+u*dy(1)/factorial(i);
end
f = [f, fi]; end
end
|
Упражнение2 |
. Длявыполненияупражнениявыбратьфункциюизтаблицыконцелабор |
|
|
|
|
|
|
а- |
||||||
торабн,сойответствтыномеркомпьютера. ующую |
|
|
|
|
|
|
|
|
|
|
|
||||
|
Для компьютеровснечетнномеромдляыполнения |
|
|
|
|
|
|
заданияиспользуетсямногочленЛ |
|
а- |
|||||
гранжа,счетнымномером |
|
– многочленНьюто. |
а |
|
|
|
|
|
|
|
|
|
|||
|
1) Создатьмассив |
изравноотстоящих5 |
значенийргумента |
|
|
x=linspace(a, b, 5) исоответств |
у- |
||||||||
ющийемассивузначефункцииий |
|
|
|
|
.Сиспользованиемпроцедуры |
|
|
-функции изпримера 2или |
|||||||
3взависимости( отварианта) |
|
полученмассиванайтиз ачениеинтерполяционногоымполин |
|
|
|
|
|
о- |
|||||||
|
, = + 0.4 |
( ) |
|
|
( ) |
|
|
|
|
||||||
значениеполинома . |
− |
|
|
|
|
Записать в файлотчета |
|
||||||||
мав |
о внутреннейточке |
|
|
|
|
, несовпадузламисетк. ющей |
|
|
|
|
|||||
|
− |
|
теоретическое значениефункции |
|
|
иполученношибкинтерполяцииую |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2) |
Найтизначениянтерполяционногополинома |
|
|
|
t=linspace(a, b, |
|
|
,построенного |
по значениям, |
|||||
вычисленнымпункте |
|
1,вовсехточках |
|
|
|
100),сравнитьполучензначеныеия |
|
|
|||||||
|
|
|
|
|
( ) |
t |
|
|
|
||||||
теоретическими.Записать |
|
в файлотче |
та:длякакогозн ченияргумента |
|
|
|
получиласьнаибольшая |
|
|||||||
ошибка |
величину этой ошибки. |
|
|
|
|
|
|
= |
− |
|
|
||||
|
3) Построграффуношибкиктьинтерполяции |
|
|
|
|
|
|
длязначений, |
|
||||||
полученныхнапр |
едыдущем шаге. |
|
|
|
|
|
|
|
|
||||||
|
4)Пользуясьграфикисходнойфункциимбъяснить |
|
|
|
|
|
|
|
соотзначенийошениеибок |
|
|
||||
интенаразличныхполяцииинтервалотрезк. ах |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
5)Повторитьпункты1 |
- 4длявходногомассиваиз8 ченийргумента |
|
|
|
|
x=linspace(a, b, 8). |
||||||||
Сравнитьошибкиинтерполяции,получеазчислевходныхныеомузлов. |
|
|
|
|
|
|
|
|
|
|
|
||||
4. Реализация интерполяциивстроенными |
|
функциямиMATLAB |
|
|
|
||||||||||
Дляод номернойинтерполяциивMATLABсуществует |
функция interp1,котподдерживрая |
а- |
етнесколькометодовинтерпметод( дляиспользовляцииможновыбратьмощьюнеобязния |
|
а- |
тельногопараметрафункции)Подробное. оп |
|
исаниефункцииможно |
|
прочитать, |
вызвав |
MATLAB |
||||
команду doc interp1. |
|
|
|
|
|
|
|
|
||
Упражнение3 |
. Длявыполненияупражнениявыбратьфункциюизтаблицыконцелабор |
|
|
|
|
|
|
а- |
||
торнойраб,соответствтыномеркомпьютера. ующую |
|
|
|
|
|
|
|
|||
1)Создатьмассив |
|
значенийргумента |
x=linspace(a, b, 8), соответствующиймассивзнач |
е- |
||||||
нийфункции |
|
,массивновыхзн ченийргумента |
|
t=linspace(a, b, 100). |
|
|
|
|||
графикеомтобратеоретзависимостьитьческую |
|
|
|
|
ирезультатинтерполяции, |
|
||||
2)Наодн |
( ) |
|
interp1 помассивам |
|
|
|
|
|||
полученспомощьюфункцииый |
|
|
Сравните3 |
-4методаинтерполяции |
д- |
|||||
держиваемыхфункцией |
|
|
interp1. |
|
(x, y). |
( ) |
|
|
|
|
Задлявыполненияаниялабораторнойработы.
№ |
|
|
y(x) |
a |
b |
№ |
|
y(x) |
a |
b |
||||
вар-та |
|
|
вар-та |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
0.5 ! + 8 !! + 8 |
-4 |
-1 |
15 |
x2 − 2x +16(x −1)−1 −13 |
2 |
5 |
|||||||
2 |
(1+ x)(x2 + 3)−1 |
-9 |
9 |
16 |
(1 + x3 )e−x |
-2 |
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
10e−x (x3 − 2x +1) |
-2 |
2 |
17 |
(1 + x) |
|
|
-3 |
3 |
|||||
8 − x |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
4 |
(1 + x2 ) sin 2x |
-1 |
5 |
18 |
(x 2 + 7x + 7)(x 2 − 2x + 2)−1 |
2 |
5 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5 |
exp(−0.5x cos x) |
-5 |
3 |
19 |
(2x 2 + 6)(x 2 |
− 2x + 5)−1 |
-3 |
3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6 |
exp(2.5 sin x) cos x |
1 |
3 |
20 |
x(2x 2 |
+1)−1 |
-1 |
4 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
7 |
x 2 sin(2x − 3) |
0 |
4 |
21 |
(1 + x) sin x |
0 |
5 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
8 |
|
x(x 2 + 3)−1 |
-5 |
5 |
22 |
exp(−x sin 2x) |
-2 |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
9 |
(1 + x 2 )(1 + x3 )−1 |
0 |
4 |
23 |
(1 − x)(x 2 + 4)−1 |
-2 |
3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
10 |
(x − 3) cos2 x |
-3 |
3 |
24 |
|
|
cos 2x |
0 |
4 |
|||||
|
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
11 |
|
(1 − x) cos x |
0 |
4 |
25 |
x 2 cos(x +1) |
-3 |
3 |
||||||
|
|
|
|
|
|
|
|
|
|
|||||
12 |
|
|
− cos(1.5x) |
0 |
8 |
26 |
x + 3 cos2 x |
-3 |
3 |
|||||
|
x |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||
13 |
sin 2x − 0.2x 2 |
0 |
6 |
27 |
x 2 + 2(x + 0.5)−1 |
0 |
4 |
|||||||
|
|
|
|
|
|
|
|
|||||||
14 |
(x 2 +1)−1 sin(x +1) |
-3 |
2 |
28 |
(x 2 +1)−1 cos x |
-2 |
3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|