
Практикум 1 (Численные методы) - Погрешность численных методов
.pdf
|
|
Практикум1. |
Погрешностьчисленныхметодов. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
Структурапогрешностивчисленныхметодах. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Распространениеошибокввычислительныхпроцедурах |
|
|
|
|
|
. |
|
|
|
|
||||
|
При численномрасчетемодели |
|
|
|
наошибку |
(погрешность) |
полученного результата влияютн |
е- |
|||||||||
сколькофакт: ров |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1) |
Ошибка физическойили |
|
математическоймодели |
|
|
– ошибканеучтенных |
свойствили |
парамет- |
|||||||||
|
ровфизиче скогоявления. |
|
Припостроении |
математической моделиневозможно |
|
учестьвсе |
|
||||||||||
|
фа,котторымвлиятьрыегутна задультограничиваются.Какпрчи,авилотолько |
|
|
|
|
|
|
|
|
|
е- |
||||||
|
сколькиминаиболеезначимымифакт,чтоопределяетрамиточностьнепосредственном |
|
|
|
|
|
|
|
|
|
о- |
||||||
|
дели. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
Ошибкавходданных |
|
|
|
– ошибкаизмепараметровфизическойениймодели |
|
|
|
|
|
|
|
(втомчисле |
|
|||
|
физическихконстант) |
|
|
|
.Вомногфизическихтехническихзадапогрешностьннаячах |
|
|
|
|
|
|
|
|
|
|||
|
может достигать несколькпроцентов.Онаиктакхводитназываемойнеустранимойп |
|
|
|
|
|
|
|
|
о- |
|||||||
|
греш,котнуправляетсяораястиматематически,зачастую, |
|
|
|
|
|
может приводить кпарадо |
к- |
|||||||||
|
сальнымрезультатам. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3) |
Ошчислбкаметоданного |
|
|
|
– связанатем,чтоисходныеоператорызам няют |
|
|
|
|
|
сяприближе |
н- |
|||||
|
ными.Например, нтегралзамекоинтегральнойяютечной |
|
|
|
|
суммой,дифференцирование |
- |
||||||||||
|
конечраз,функциюностьюй |
|
|
|
– полиномом,бесконечныйряд |
|
|
– конечнойсуммойэлементов. |
|
|
|||||||
|
Численный методобычно |
|
выбирают такимобраз,чтобыегоп мгрешностьбыла |
|
|
|
|
|
в2 -4 раза |
||||||||
|
(на1 -2двоичныхразряда) |
|
|
|
меньшенеустранимойпогрешности. |
|
|
|
Делатьпогрешностьм |
еньше |
|||||||
|
невыгодноиз |
-заувеличенияобъемавыполняемыхвычислений,больше |
|
|
|
|
|
– из-заснижениято |
ч- |
||||||||
|
ностивычислений.Ош бкам управляетсятоданногоматематически. |
|
|
|
|
|
|
|
|
|
|
||||||
4) |
Ошибкаокругления |
– связанаограниченразрядсеткойкомпьютераной |
|
|
|
|
|
|
(вычислительн о- |
||||||||
|
гоустройства)иотбрасываниеммлраздшприпредставленииядовхпромежуточных |
|
|
|
|
|
|
|
|
|
е- |
||||||
|
зультатоввычислений |
|
|
,из -зачего,например,бесконечныедесятичныедробипредставляются |
|
|
|
|
|
|
|
||||||
|
вконе чномвиде. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Задачапостроенияфизическойматематическоймоделей |
|
|
|
|
находитсязарамкаминашегоку |
|
|
|
|
р- |
||||||
са,поэтомуостанаошибквливмодмынбудемали.Остальныетьсяхвидыошибокмырассмо |
|
|
|
|
|
|
|
|
|
|
|
т- |
|||||
римподробнееалее. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. |
Ошибкавходданных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ВлияниеошибкивовходданрезультатныхвычирасналениясмотримпримереУи |
|
|
|
|
|
|
|
|
|
|
л- |
|||||
кинсона. |
Рассмотримполино |
|
. |
! = − 1 − 2 − |
. Очевид,чток егорнямиявляюо |
|
|
|
|
т- |
|||||||
(при ! = 1, ! = 2, … , ! = |
|
Изменим значение одногоизегок эффиц,напр,второгимерентов |
|
|
|
|
|
о |
|||||||||
ся |
|
n-1) |
|
|
|
|
|
|
|
|
|||||||
степени |
нанекоторуюмалуювеличину.Значекорполиноприияейэтомз . енятсяа |
|
|
|
|
|
|
|
|
|
|
||||||
Дляполиномнизкойстепениэтизменевеличинойсравнипоправкимокоэффициенте.Но |
|
|
|
|
|
|
|
|
|
|
|
||||||
ужепристепенипорядизменен20 корнейаповелбудетисравнимочине |
|
|
|
|
|
|
|
|
|
созначениемсамого |
|
||||||
корня,болеетогочастькорнейстанеткомплекснымичислами. |
|
MATLAB значения |
|
= |
− 1 |
− 2 |
= |
! |
− 3 + 2. |
|
|||||||
|
Нахсподиммощью |
|
|
|
|||||||||||||
|
Пример 1. Рассмотримполином |
второй степени |
|
! |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
коэффициентов. |
|
|
|
|
|
|
|
|||
|
>> n=2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
>> c=(1:n)'; |
|
|
%Наборзначекориснийе |
|
|
ходногополинома |
|
|
|
|
|
|||||
|
>> p=poly(c) |
|
|
%Нахкоэффициентыдимполинегкорнямма |
|
|
|
|
|
|
|
|
|
|
|||
|
p = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
-3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
>> ps=poly2sym(p) |
%Полиномвсимвольномвиде |
|
|
|
|
|
|
|
|
|
|
|||||
|
ps = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x^2 - 3*x + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
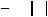
Дляпроверкинах полученногорнидмногочленаиубеждаемся,чтоонисовпадают
теоретическими:
>>r=sort(subs(solve(ps)))
r =
1
2
>>err1=r-c
err1 = |
|
|
0 |
|
|
0 |
|
!!" иповторяем ы- |
Изменяемзначениевторогокоэффициентамногочлена |
навеличину |
|
числение корней: |
|
= 2 |
>> err=2^-30 |
%Значениепогрешн,вносимойк эффициентсти |
|
err = |
|
|
9.313225746154785e-10 |
|
|
>> p(2)=p(2)+err; |
%Добавляемпогрешностьвовторойкоэффициент |
|
>>ps=poly2sym(p);
>>r=sort(subs(solve(ps)))
r =
1.000000000931323e+00
1.999999998137355e+00
>>err2=r-c
err2 = 9.313225746154785e-10
-1.862645149230957e-09
Массив err2 содержитпогрешностивычислениякорнеймод фицполином.В р ванного |
|
д- |
|
но,чтомаксимальнаяошибк |
авсегодварвызаошкоэффициентаибки,что |
впринципе некр |
и- |
тично. |
|
|
|
Упражнение1. |
Повторитедействияизпридл1многочленоверастепени |
n=10, 15, 20. |
|
Сравнитепогрешностьвычикорсозленияаченияей |
|
мипоправкикоэффициенте. |
|
Замечание.Привыполненииупражнениядля1 |
n=20 вычискорнейдисходноголяениеп |
о- |
|
линмовыпжетмасошибкамилняться.Этосвязанотем,чторазряднчисл( знаков)младшихсть |
|
|
|
коэффициентов достигаетразрядностикомпьютера. |
|
|
|
2. Влияниеошибококруглениянарезультат |
ы вычислений |
|
|||||||
|
Действительныечислахранятсяпамятикомпьютформ«плавающейзапятойра»: |
= !, |
|
|
|
|
|
|
|
где f – мантиссачисла |
x, удовлетворяющаяусловию |
< 1 |
, |
= 2 |
– основаниеси числтемы |
е- |
|||
нияво( сеховрекомиспользуетенныхпьютерахдво чнаячитема),сления |
!! ≤ |
|
|
– порядок |
|||||
числа. |
Дляхраненпорядкаманти числаотводитсяыфиксч двоичныхрслоразрядовванное. |
|
|
|
|
|
|
||
|
В MATLAB намантиссучислаотводится52двоичныхразряд |
|
|
|
|
а,что соответствуетпримерно |
|
||
16десятичнымзнакпослеа.пятойЕсличисло |
|
содержитбольшееколичествозна |
|
ков,то |
происхо- |
||||
дитокругленмантиссыдонужногочисларазрядове |
|
. |
|
|
|
|
|
|
|
|
Казалбы,такаяочносьпредставлетьпосудобнавлетворитьлюбыенуждыияисследов |
|
|
|
|
|
|
а- |
|
теля.Однаконеобходп ,чтомн,наип,мотьриередтекакмдвачислаербудутсложены |
|
|
|
|
|
|
, они |
||
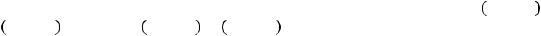
должныбытьприведеныкединомупорядку,ато,чтоприсложениивыйдетзаманбудетиссу |
|
|
10 |
! |
+ 10 |
!! вмантиссууложатся15десятичныхзна |
|
|
|
|
|
т- |
||||||||||||||||||
брошено!Поэтому, сложить |
|
|
|
|
|
|
|
|
|
ковибудетп |
|
о- |
||||||||||||||||||
лученверезультат,ыйесливыполнить |
|
|
|
|
|
10! + 10!! |
,томалоечисловыйдетзаразряднуюсетку,и |
|
|
|
|
|
|
|||||||||||||||||
получимтеже |
|
10 |
! (проверьте)Получ. параситуацияетсядоксальная |
|
|
|
– давайтеприбкм1 лоевим |
|
|
|||||||||||||||||||||
число |
!!", |
|
|
|
|
|
|
!" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
дов – |
10 |
последовательно |
|
10 |
|
|
разтакие( вычи |
|
|
|
|
сленияхарактерныдлязадач |
|
|
|
численныхмет |
о- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
вычислениерядов,разнообраит раци,разнныеадачио…Легкостныенайти). ответ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
|||||||
11,однмашиннаяко |
|
|
рифметикадает1 |
|
|
|
– ошибка1000%. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Пользуясьприведеннойвыше |
|
|
|
|
|
|
информацией, |
|
попробуйтепредсказатьрез |
|
|
ультатвдвухслед |
|
у- |
|||||||||||||||
ющихупражненияхпроверьтевывс компьютеращьюды. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Упражнение2. |
Рассмотрим выражение |
!! |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 + − 1 |
|
, = 0,1,2, … |
|
|
|
|
|
|
||||||||||||
|
Сточкизреаналитическойияматематикизначениеэтоговыраженияпостояравноед но |
|
|
|
|
|
|
, = 2 |
|
|
|
|
|
|
|
и- |
||||||||||||||
ницедлюбыхя |
|
n. Будетлив |
|
ыполнятьсяравенствопривычислениинакомпьютере? |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Сделайтепредпол,прикакзначожмениия |
|
|
|
|
|
|
|
|
|
|
|
|
|
n этовыражперотлестанетедотичаться |
|
|
|
|
и- |
||||||||||
ницы,чемубудетравно;напишитерограмму,реализэтоталгоритмспошаговойющуювыдаче |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
номерашага,зн чения |
|
|
|
|
и результатавыражения. |
|
|
|
|
, |
|
|
|
|
, |
|
, |
|
|
|
|
|
||||||||
|
Упражнение3 |
Найтисуммучисел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n – целоечисло) |
. |
||||||||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
! = 2! |
|
! = − ! |
|
! = 2!! |
|
! = − ! |
|||||||||
Значение вычислить, |
используяразличныйпорсуммированиядокслагаемых: |
|
|
|
|
|
|
|||||||||||||||||||||||
!) = ! + ! + ! + ! |
|
= ! + ! + ! + ! |
|
|
|
|
|
значениеивая |
|
n, |
||||||||||||||||||||
, |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
Последовательноувели |
= ! + ! |
+ ( ! + |
||||||
определитеприкаком |
|
|
|
минимальном n,значения |
A, B и C будутразличаться. |
|
|
|
|
|
|
|||||||||||||||||||
|
Повторитеэкспериментдляоснованиястепени10 ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! = 10!, ! = 10!!)Прикаких. значениях |
|
|
||||||||||
nрезультатыстановятсяразличными?
3.Правилаокруглениячисел
Вкомпьютерахобычнореализовано |
|
симметричокруглениое |
|
последующемуправилу:если |
|
|
||||
встаршемотбрасываем |
|
|
ом разряде стоитцифраменьшаяпяти,тосодержимоесохразрядовнямых |
|
|
|
|
|||
числанеизменяется.Впротивнслучмлсаоедшиймхрадобавляетзрядняемый |
|
|
|
|
сяединицастем |
|
||||
жезнак,чтиусаомчисла.Краткоогоэтоправилоформулируюттак: ругление |
|
|
|
|
доближайшего |
|||||
целого. |
|
|
|
|
|
|
|
|
|
|
Существуютидругиеправилаокругления,осуществпорешениюпользователяяемыеЭВМ. |
|
|
|
|
|
fix, ceil, |
||||
На,впакетеример |
|
|
MATLAB реализованочетыреспециал |
ьныекомандыокруглениячисел: |
|
|||||
floor, round. Команда round соответствует описанномувышеокр |
|
углендоближайшегоцелогою, |
|
ко- |
||||||
манда fix находитцелуючас ь |
|
числа, |
отбрасываявсюдробнуючасть,команды |
|
ceil и floor находят |
|||||
ближайшеецелое,которое |
|
|
|
большеилименьшезаданнчисла,соответственного. |
|
|
|
|
||
Округчисладо ение |
|
k знаковпослезапятой |
можнореализоватьспомд полнительногощью |
|
|
|||||
умноженийа |
10 |
! и |
!!,например,ввиде(10 |
|
^(-k)*round(10^k*x)) (вместокоманды |
round может |
||||
использоватьсялюбаяд |
|
|
10ругаякомандаокругления). |
|
|
|
|
|
|
|
Упражнение4. |
|
Поисравнитьтроивек[ оры |
|
round(x) fix(x) ceil(x) floor(x)]дляраззных |
а- |
|||||
чений х: |
|
|
|
|
|
|
|
|
|
|
11.2, -11.2 4.5, -4.5, 55.6, -55.6. |
|
|
|
|
|
|
||||
Опредазносмеждуисходнымлизначть результатаминиемокруглен.Какойметодя |
|
|
|
|
|
|
||||
округлениядаетнаименьпогрешностьую |
|
(длюбяпроизвольногочисла) |
? |
|
|
|||||
4. Ошчисленногобкаметода
Появлениеошибки |
численного методаобычновызванотем,чтоцеляхэконовремииени |
вычисленийточныефорзаменяютсяулы |
приближенными.Данныеошибкиможко тролировать |

привычислен,например,выббольшеечислояхраяслагаемыхпривычрядаилислениименяяп |
|
о- |
|
рядоквычислений.Рассмпоявлензаменышибкитримнапр ресконечногорядаконечным. |
|
|
|
Упражнение5. |
Вкурсем |
атематическогоанализарассматриваласьформуладлявычисления |
|
синусачислапомощьюрядаМ :клорена |
|
! −1 ! !!!! |
|
|
|
||
|
|
sin ≈ !!! |
2 + 1 ! . |
Реализуйтенакомпьютеревычсивслениеточкахнуса |
|
|
числе N. Постройтезависимостьпо |
грешностивычисленияотчисла |
|
ныхвышезначений |
x. |
|
Частобольшаяпогрешносчислм обуслтоданногоь,емчтонеудачныйвленапорядок численийприкувелодвлияошибоктчевходнидаяюилинокругленияныхпри нииметода.Рассмотрим алгорвычислениянтегралатм
!! , !! , спомощьюрядапризаданном |
н- |
N ввидеграфикадлявсехзада |
ы- использова-
|
|
|
! = |
|
! ! !!! , = 1,2,3, … |
|
|||||||||
Заметьте,чтоп дынтегральнаяфункцвсемотрезкеинтегрированиянеотрицательна, |
! |
|
|
|
|
|
|
|
|
||||||
следовинтегралально,изначение |
|
|
|
– положительноечисло.Болеетого,под |
|
|
|
|
ынтегральнаяфункция |
||||||
наданинтеогмрфункциейвалеаничена |
|
|
|
|
|
|
= 1 |
,т.е.значениеинтможгралапредвышать |
и- |
||||||
ницы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ксожалению,первообразнуюдлядан тогогралавозможновыразитьвидеэл мента |
|
|
|
|
|
|
|
|
|
|
|
р- |
|||
нойфункции.Однакосуществуетвозмполучитьжность |
|
|
|
|
|
|
|
|
|
|
|
рекуррентнформулдляопределенногоую |
|||
интеграла. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Интегрируяпочастям,находим: |
|
! = |
! |
|
!!! |
= |
!!! |
! |
|
! |
!!! |
= |
|||
|
|
|
|
||||||||||||
|
|
! |
|
|
|
|! − |
! |
|
, |
||||||
! = |
! |
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
! ! !!! = ! !!!|!! − 2 |
! !!! = 1 − 2 !, |
||||||||||||||
! = |
! |
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
! ! !!! = ! !!!|!! − |
! !!! !!! = 1 − !!!. |
||||||||||||||
Есливычислятьзначениеинтегралааналитически,подставляязначениеинтеграловмладшей« степени»ввидеформулы,товычислениябудутпроисходитьбезошибок.Вследующемупражнении
мырассмотримвычислениедан тегралыхрекуррентночетомтого,чтовз начениеэкспоненты вкомпьютерехранитсявприближенномвиде.
Упражнение6. |
|
|
,затем ! = ! |
|
! |
|
!!! |
|
|
≤ 30 |
|
|
|
||
1) Вычислитезначенияинтеграла |
|
|
привсех |
,используярекуррентную |
|||||||||||
|
|
|
|
! |
|
|
|
|
|||||||
процедуру,т..сначалавычислив |
константы! |
! |
используянайденноезначение |
|
! |
,ит |
акдалее. |
||||||||
|
|
|
|
|
|
|
|
|
|
e. |
|||||
2) Повычисленияторите,используясимвольныепеременные,томчисле,для |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Посм,какогласутрите |
ютсяполученны |
е результаты.Попытайтнаосновеполученныхсь |
|
||||||||||||
сведенийопогрешностяхобъясданныйфеномен.ить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
