46. Алгоритм обратного распространения ошибки

Алгоритм обратного распространения ошибки определяет стратегию подбора весов многослойной сети с применением градиентных методов оптимизации. «Изобретенный заново» несколько раз, он в настоящее время считается одним из наиболее эффективных алгоритмов обучения многослойной сети. Его основу составляет целевая функция, формулируемая, как правило, в виде квадратичной суммы разностей между фактическими и ожидаемыми значениями выходных сигналов.

В случае единичной обучающей выборки (x, d) целевая функция определяется в виде 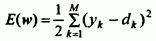(51)

При большем количестве обучающих выборок j (j=1, 2, …, p) целевая функция превращается в сумму по всем выборкам

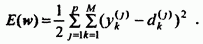(52)

Уточнение весов может проводиться после предъявления каждой обучающей выборки (так называемый режим “онлайн”) либо однократно после предъявления всех выборок, составляющих цикл обучения (режим “оффлайн”). В последующем изложении используется целевая функция вида (51), которая соответствует актуализации весов после предъявления каждой выборки.

1. Для упрощения можно считать, что цель обучения состоит в таком определении значений весов нейронов каждого слоя сети, чтобы при заданном входном векторе получить на выходе значения сигналов y_i, совпадающие с требуемой точностью с ожидаемыми значениями d_i при i=1, 2, …, M.

47. Этапы алгоритма обратного распространения ошибки

Обучение сети с использованием алгоритма обратного распространения ошибки проводится в несколько этапов. На первом из них предъявляется обучающая выборка х и рассчитываются значения сигналов соответствующих нейронов сети. При заданном векторе x определяются вначале значения выходных сигналов v_i скрытого слоя, а затем значения y_i нейронов выходного слоя. Для расчета применяются формулы (49) и (50).

После получения значений выходных сигналов y_i становится возможным рассчитать фактическое значение целевой функции E(w) заданной выражением (51). На втором этапе минимизируется значение этой функции.

48. Градиентные алгоритмы обучения сети

Если принять, что целевая функция непрерывна, то наиболее эффективными способами обучения оказываются градиентные методы оптимизации, согласно которым уточнение вектора весов (обучение) производится по формуле где η – коэффициент обучения, p(w) – направление в многомерном пространстве w.

Обучение многослойной сети с применением градиентных методов требует определения вектора градиента относительно весов всех слоев сети, что необходимо для правильного выбора направления p(w). Эта задача имеет очевидное решение только для весов выходного слоя. Для других слоев создана специальная стратегия, которая в теории ИНС называется алгоритмом обратного распространения ошибки (error backpropagation), отождествляемым, как правило, с процедурой обучения сети. В соответствии с этим алгоритмом в каждом цикле обучения выделяются следующие этапы:

1. А нализ нейронной сети в прямом направлении передачи информации при генерации входных сигналов, составляющих очередной вектор х. В результате такого анализа рассчитываются значения выходных сигналов нейронов скрытых слоев и выходного слоя, а также соответствующие производные

функции активации каждого слоя, где m – количество слоев сети.

2. Создание сети обратного распространения ошибок путем изменения направлений передачи сигналов, замена функций активации их производными и подача на бывший выход (а в настоящий момент - вход) сети возбуждения в виде разности между фактическим и ожидаемым значением. Для определенной таким образом сети необходимо рассчитать значения требуемых обратных разностей.

3. Уточнение весов (обучение сети) производится по предложенным выше формулам на основе результатов, полученных в п. 1 и 2, для оригинальной сети и для сети обратного распространения ошибки.

4. Описанный в п. 1, 2 и 3 процесс следует повторить для всех обучающих выборок, продолжая его вплоть до выполнения условия остановки алгоритма. Действие алгоритма завершается в момент, когда норма градиента упадет ниже априори заданного значения ε характеризующего точность процесса обучения.

Для сети с одним скрытым слоем

Рассмотрим условия, относящиеся к сети с одним скрытым слоем. Используемые обозначения представлены на рис. 19 (уже был ранее).

Как и ранее, количество входных узлов обозначим буквой N количество нейронов в скрытом слое К, а количество нейронов в выходном слое М. Будем использовать сигмоидальную функцию активации этих нейронов. Основу алгоритма составляет расчет значения целевой функции как квадратичной суммы разностей между фактическими и ожидаемыми значениями выходных сигналов сети. В случае единичной обучающей выборки (x,d) целевая функция задается формулой (51), а для множества обучающих выборок j (j=1, 2, …, p) – формулой (52).

Для упрощения излагаемого материала будем использовать целевую функцию вида (51), которая позволяет уточнять веса после предъявления каждой обучающей выборки.

Эта функция определяется выражением:

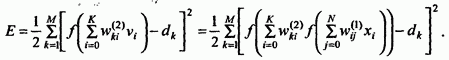(53)

Конкретные компоненты градиента рассчитываются дифференцированием этой зависимости. В первую очередь подбираются веса нейронов выходного слоя. Для выходных весов получаем:

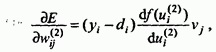где

Если ввести обозначение (54)

то соответствующий компонент градиента относительно весов нейронов выходного слоя можно представить в виде

(55)

Компоненты градиента относительно нейронов скрытого слоя определяются по тому же принципу, однако они описываются другой, более сложной зависимостью, следующей из существования функции, заданной в виде

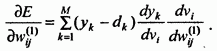(56)

После конкретизации отдельных составляющих этого выражения получаем: 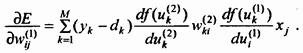(57)

Если ввести обозначение 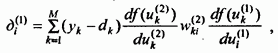(58)

то получим выражение, определяющее компоненты градиента относительно весов нейронов скрытого слоя в виде 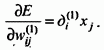(59)

В обоих случаях (формулы (55) и (59)) описание градиента имеет аналогичную структуру и представляется произведением двух сигналов: первый соответствует начальному узлу данной взвешенной связи, а второй – величине погрешности, перенесенной на узел, с которым эта связь установлена. Определение вектора градиента очень важно для последующего процесса уточнения весов.

В классическом алгоритме обратного распространения ошибки фактор p(w) задает направление отрицательного градиента, поэтому (60)

Существуют и другие, более эффективные методы выбора направления p(w).

Градиентные методы обучения сети

• Алгоритм наискорейшего спуска

• Алгоритм переменной метрики

• Алгоритм Левенберга-Марквардта

• Алгоритм сопряженных градиентов

А также:

• Эвристические методы обучения сети

• Элементы глобальной оптимизации:

  • Алгоритм имитации отжига

  • Генетические алгоритмы

• Методы инициализации весов

РАДИАЛЬНЫЕ НЕЙРОННЫЕ СЕТИ

Многослойные нейронные сети, представленные в предыдущих разделах, с точки зрения математики выполняют аппроксимацию стохастической функции нескольких переменных путем преобразования множества входных переменных во множество выходных переменных . Вследствие характера сигмоидальной функции активации осуществляется аппроксимация глобального типа. В результате ее нейрон, который был однажды включен (после превышения суммарным сигналом u_i определенного порогового значения), остается в этом состоянии при любом значении u_i, превышающем этот порог. Поэтому всякий раз преобразование значения функции в произвольной точке пространства выполняется объединенными усилиями многих нейронов, что и объясняет название глобальная аппроксимация.

Другой способ отображения входного множества в выходное заключается в преобразовании путем адаптации нескольких одиночных аппроксимирующих функций к ожидаемым значениям, причем эта адаптация проводится только в ограниченной области многомерного пространства. При таком подходе отображение всего множества данных представляет собой сумму локальных преобразований. С учетом роли, которую играют скрытые нейроны, они составляют множество базисных функций локального типа. Выполнение одиночных функций (при ненулевых значениях) регистрируется только в ограниченной области пространства данных – отсюда и название локальная аппроксимация.

Особое семейство образуют сети с радиальной базисной функцией, в которых скрытые нейроны реализуют функции, радиально изменяющиеся вокруг выбранного центра и принимающие ненулевые значения только в окрестности этого центра. Подобные функции, определяемые в виде φ(x)= φ(||x-c||) будем называть радиальными базисными функциями. В таких сетях роль скрытого нейрона заключается в отображении радиального пространства вокруг одиночной заданной точки либо вокруг группы таких точек, образующих кластер. Суперпозиция сигналов, поступающих от всех скрытых нейронов, которая выполняется выходным нейроном, позволяет получить отображение всего многомерного пространства.

Сети радиального типа представляют собой естественное дополнение сигмоидальных сетей. Сигмоидальный нейрон представляется в многомерном пространстве гиперплоскостью, которая разделяет это пространство на две категории (два класса), в которых выполняется одно из двух условий: либо либо

Такой подход продемонстрирован на рис. 20 а).

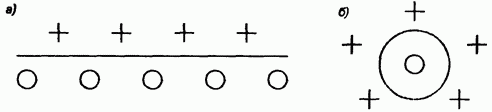
Рис. 20. Иллюстрация способов разделения пространства данных:

а) сигмоидальным нейроном; б) радиальным нейроном

В свою очередь радиальный нейрон представляет собой гиперсферу, которая осуществляет шаровое разделение пространства вокруг центральной точки (рис. 20 б). Именно с этой точки зрения он является естественным дополнением сигмоидального нейрона, поскольку в случае круговой симметрии данных позволяет заметно уменьшить количество нейронов, необходимых для разделения различных классов.

Поскольку нейроны могут выполнять различные функции, в радиальных сетях отсутствует необходимость использования большого количества скрытых слоев. Структура типичной радиальной сети включает входной слой, на который подаются сигналы, описываемые входным вектором х, скрытый слой с нейронами радиального типа и выходной слой, состоящий, как правило, из одного или нескольких линейных нейронов. Функция выходного нейрона сводится исключительно к взвешенному суммированию сигналов, генерируемых скрытыми нейронами.