40. Обучение линейного нейрона по правилу Ойя

Нестабильность правила Хебба в процессе обучения можно устранить ограничением вектора весов за счет операции ренормализации, т.е. таким подбором пропорционального коэффициента α на каждом шаге обучения, чтобы w’= αw при ||w’||=1. Этот метод достаточно сложен и требует дополнительных трудозатрат на этапе обучения.

Е.Ойя модифицировал правило Хебба таким образом, что и без ренормализации процесса обучения вектор весов самостоятельно стремится к ||w||=1. В соответствии с правилом Ойи уточнение весов производится согласно выражению (38)

Это правило напоминает обратное распространение, поскольку сигнал х_i модифицируется обратным сигналом, связанным с выходным сигналом y нейрона. Для каждого отдельно взятого нейрона правило Ойя может считаться локальным, так как в процессе модификации х_i принимается во внимание только тот весовой коэффициент, значение которого подбирается в текущий момент времени.

Доказательство ограниченности весов, уточняемых по правилу Ойя, можно получить, заменяя скалярное выражение (38) векторной формой, которая с учетом упрощения η=1 и в соответствии с (38) приобретает вид: (39)

Стабильность процесса обучения достигается, когда при достаточно длительном обучении обеспечивается ||Δw||=0, т. е.

(40)

Результат применения правила Ойя

Итак, доказательство ограниченности весов, уточняемых по правилу Ойя, можно получить, заменяя скалярное выражение (38)

векторной формой (39)

Стабильность процесса обучения достигается, когда при достаточно длительном обучении обеспечивается ||Δw||=0, т. е.

(40)

Если собственное значение корреляционной матрицы С обозначить λ, а вектор w подбирать как связанный с ней собственный вектор, то по определению собственного значения имеем Cw = λw. Подставляя это выражение в формулу (39), получаем

(41)

Из (41) следует, что применение для обучения модифицированного правила Хебба приводит к ограничению модуля вектора w единицей

| w | =1, обеспечивающему ограниченность значений весовых коэффициентов.

Стохастическая модель нейрона

В отличие от всех детерминированных моделей, определенных ранее, в стохастической модели выходное состояние нейрона зависит не только от взвешенной суммы входных сигналов, но и от некоторой случайной переменной, значения которой выбираются при каждой реализации из интервала (0,1).

В стохастической модели нейрона выходной сигнал y_i принимает значения ±1 с вероятностью Prob(y_i = ±1) = 1/(1+exp(±2βu_i)), где u_i обозначена взвешенная сумма входных сигналов i-го нейрона, а β – это положительная константа, чаще всего равная 1. Процесс обучения нейрона в стохастической модели состоит из следующих этапов:

1. Расчет для каждого нейрона сети взвешенной суммы

2. Расчет вероятности того, что у_i принимает значение ±1 в соответствии с формулой

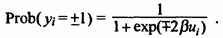
3. Генерация значения случайной переменной R ϵ (0,1) и формирование выходного сигнала y_i = ±1, если R < Prob(y_i = ±1) или в противном случае.

Определенный таким образом процесс осуществляется на случайно выбранной группе нейронов, вследствие чего их состояние модифицируется в соответствии с предложенным правилом.

4. После фиксации состояния отобранных нейронов их весовые коэффициенты модифицируются по применяемому правилу уточнения весов. Например, при обучении с учителем по правилу Видроу-Хоффа адаптация весов проводится по формуле

Доказано, что такой способ подбора весов приводит в результате к минимизации целевой функции, определенной как среднеквадратичная погрешность

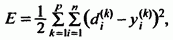
рассчитываемая по всем n нейронам и p обучающим выборкам.