Отчет по практическим

МИНОБРНАУКИ РОССИИ федеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)» (СПбГЭТУ «ЛЭТИ»)

отчет

по практическим работам

по дисциплине «Безопасность ИТС»

Студент гр. 5374		Уруков С.Д.
Преподаватель		Молдовян Н.А.

Оглавление

Цель работы 3

Задача №1 “Система открытого распределения ключей Диффи – Хеллмана” 3

Задача №2 “Открытое распределения ключей с использованием криптосистемы RSA” 7

Задача №3 “Генерация больших простых и псевдопростых чисел” 11

Цель работы

Предлагаемые темы для выполнения практических работ направлены на закрепление материала, относящегося к двух ключевой криптографии – схемам открытого распределения ключей, открытому шифрованию и системам цифровой электронной подписи.

Задача №1 “Система открытого распределения ключей Диффи – Хеллмана”

Теоретическая часть

В данной криптосистеме каждый абонент выбирает случайный секретный ключ x и вырабатывает открытый ключ y в соответствии с формулой

y = ^x (mod p).

Все абоненты размещают свои открытые ключи в общедоступном справочнике, который должен быть заверен специально созданным доверительным центром, чтобы исключить возможные нападения путем подмены открытых ключей или навязывания ложных открытых ключей. Если два абонента A и B хотят установить секретную связь, то они поступают следующим образом. Абонент A берет из справочника открытый ключ абонента B и, используя свой секретный ключ, вычисляет общий секретный ключ:

Z_AB = (y_B)^x_A = (^x_B)^x_A = ^x_B^x_A (mod p),

где y_A и y_B  открытые ключи абонентов A и B; x_A и x_B  соответствующие секретные ключи. Общий секретный ключ Z_AB нет необходимости передавать по сети связи, поскольку абонент B по известному из справочника открытому ключу абонента A аналогичным способом вычисляет значение

Z_AB = (y_A)^x_B = (^x_A)^x_B = ^x_B^x_A (mod p).

Предполагается, что оппоненту (потенциальному нарушителю) могут быть известны значения y_B = ^x_{B (}mod p) и y_A = ^x_{A (}mod p), передаваемые по открытому каналу, но для того чтобы вычислить Z_AB, он должен решить трудную задачу дискретного логарифмирования. Общий секрет Z_AB может использоваться абонентами для шифрования сеансовых секретных ключей, а последние  для шифрования сообщений с использованием симметричных методов шифрования.

Практическая часть

Выбраны следующие числа в качестве секретных ключей. Для случайных пользователей генерируется открытый ключ.

p	8384380451
α	13
Пользователи	x	y
Marchuk	15	51185893014090700
Schworer	16	665416609183179000
Lachat	17	8650415919381330000
Kryshak	12	23298085122481
Leopoldo	21	247064529073450000000000
Soelberg	13	302875106592253
Liz	1	13
Appelgate	16	665416609183179000
Trethaway	19	1461920290375440000000
Kyung	10	137858491849

Результирующая таблица прилагается ниже. Вычисления произведены с помощью написанной программы на языке Python.

Таблица 1 – Результирующая сводка по всем пользователям

	Marchuk	Schworer	Lachat	Kryshak	Leopoldo	Soelberg	Liz	Appelgate	Trethaway	Kyung
Marchuk	5534722101	2706651759	6103824627	3550363844	7958017271	7718771701	4954976347	2706651759	8215090286	8080040857
Schworer	2706651759	3890296092	3769382978	7273538248	779549713	4051478759	5724029354	3890296092	444853562	7312689903
Lachat	6103824627	3769382978	2691117662	7041776736	3271672985	2254151039	7337337994	3769382978	5424470624	8121314172
Kryshak	3550363844	7273538248	7041776736	2181447755	674444599	4669922360	6276229603	7273538248	2432801947	2313078824
Leopoldo	7958017271	779549713	3271672985	674444599	465728287	7080076459	2505454340	779549713	951313349	5565093740
Soelberg	7718771701	4051478759	2254151039	4669922360	7080076459	7719192241	6131560780	4051478759	5235020432	5933044516
Liz	4954976347	5724029354	7337337994	6276229603	2505454340	6131560780	13	5724029354	7506194689	3708404633
Appelgate	2706651759	3890296092	3769382978	7273538248	779549713	4051478759	5724029354	3890296092	444853562	7312689903
Trethaway	8215090286	444853562	5424470624	2432801947	951313349	5235020432	7506194689	444853562	6716378641	5053822271
Kyung	8080040857	7312689903	8121314172	2313078824	5565093740	5933044516	3708404633	7312689903	5053822271	1539066033

Листинг программы

p = 8384380451

alpha = 13

x_keys = [15, 16, 17, 12, 21, 13, 1, 16, 19, 10]

y_keys = [alpha**i for i in x_keys]

print(x_keys)

print(y_keys)

for x in x_keys:

for y in y_keys:

print(y**x%p, end=" ")

print()

Задача №2 “Открытое распределения ключей с использованием криптосистемы RSA”

Теоретическая часть. В криптосистеме RSA сеансовые ключи шифруются по открытому ключу получателя и распределяются по открытому каналу. Процедура зашифрования выражается формулой:

С = K ^d mod n.

Получатель расшифровывает сеансовый ключ с использованием своего секретного ключа:

K = C ^e mod n.

Однако получатель должен получить гарантии того, что расшифрованный ключ был действительно отправ-лен подлинным отправителем. Аутентификация источника сообщения требует использования открытого ключа отправителя, поэтому отправитель должен подписать посланную криптограмму по своему секретному ключу d: S = H d mod n, где H – хэш-функция от криптограммы C. Затем присоединить подпись S к отправляемому значению C. Если модуль отправителя n больше модуля получателя, то он может отправить только значение S = С d mod n, поскольку получатель, проверяя «подлинность» подписи в этом случае может восстановить значение C, а затем по своему секретному ключу расшифровать C и получить значение ключа. Однако окончательная подлинность отправителя будет установлена только после того, как отправитель правильно зашифрует или расшифрует некоторое случайное пробное сообщение. Отправитель может подписать и хэш-функцию, полученную от от значения ключа. (Подпись, полученная непосредственно по значению ключа, фактически раскрывает ключ, поэтому в открытом виде пересылаться по каналам связи не должна.)

Практическая часть

Возьмем два простых числа p и q. Для них вычислим n – модуль. Сформируем открытый и закрытый ключи e и d, такие что:

1. e – простое,

2. 

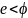
3. НОД(е,φ)=1

4. 

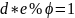
Была написана небольшая программа на языке Python, которая генерирует нужные параметры по заданным p и q.

p=157, q=727, n=114139, phi=113256, e=7207, d=46327

Программа также сгенерировала массив, содержащий 10 сообщений, которые надо закодировать. Шифрование производилось по открытому ключу e, а дешифровка по закрытому d.

data	encrypted	decrypted
87	40799	87
31	98176	31
72	37149	72
55	82206	55
42	109819	42
17	66901	17
67	42960	67
80	8077	80
40	45841	40
11	86524	11

Как результат, мы видим, что столбик data и столбик decrypted содержат одинаковые данные, что говорит о правильности выполненной процедуры.

Листинг программы, с помощью которого были произведены расчеты прикладывается ниже.

import random

def hcfnaive(a,b):

if(b==0):

return a

else:

return hcfnaive(b,a%b)

def isPrime(n):

# Corner cases

if (n <= 1):

return False

if (n <= 3):

return True

# This is checked so that we can skip

# middle five numbers in below loop

if (n % 2 == 0 or n % 3 == 0):

return False

i = 5

while (i * i <= n):

if (n % i == 0 or n % (i + 2) == 0):

return False

i = i + 6

return True

p = 157

q = 727

n = p*q

phi = (p-1)*(q-1)

while True:

e = random.randint(1, phi)

if isPrime(e) and hcfnaive(phi, e) == 1:

break

rands = 0

for d in range(5, 100000):

if d * e % phi == 1:

print()

break

rands += 1

print("\rattempts to generate d = {}".format(rands), end="")

print("p={}, q={}, n={}, phi={}, e={}, d={}".format(p,q,n,phi,e,d))

data = [random.randint(10,99) for _ in range(10)]

print("data = {} ".format(data))

encrypted = [ i**e%n for i in data ]

print("encrypted = {} ".format(encrypted))

decrypted = [i**d%n for i in encrypted]

print("decrypted = {}".format(decrypted))

print("data\tencrypted\tdecrypted")

for i in range(len(data)):

print("{}\t{}\t{}".format(data[i], encrypted[i],decrypted[i]))

Задача №3 “Генерация больших простых и псевдопростых чисел”

Теоретическая часть

Для генерации больших простых чисел могут быть использованы следующие три подхода:

• формируются случайные числа заданного размера и проверяется, являются ли они простыми, с помощью вероятностных тестов (псевдопростые числа);

• по определенной процедуре генерируются простые числа, проверка которых осуществляется с помощью детерминированных тестов на простоту;

• комбинированная генерация простых чисел, при которой формируются псевдопростые числа (по первому варианту) промежуточного размера, на основе которых затем формируются псевдопростые числа, тестируемые с помощью детерминистических тестов (этот подход обеспечивает ускорение процедуры генерации псевдо-простых чисел p с известным разложением функции Эйлера от него).

В первом случае тесты строятся на основе определенных теорем из теории чисел, сформулированных и доказанных для простых чисел. Если число не удовлетворяет тесту, то оно не является простым и отбрасывается. Для проверки берется следующее случайное число требуемого размера. Если число проходит тест, то некоторый переменный параметр, используемый для тестирования, изменяется и тест повторяется снова. Число прошедшее большое число опытов определенного типа, считается псевдопростым, поскольку вероятность, что составное число может пройти все тесты пренебрежимо мала. Для того, чтобы исключить некоторые возможные классы составных чисел, которые могут проходить тесты конкретного типа, используют несколько различных тестов, по каждому из которых выполняется большое число опытов. Достоинством генерации псевдопростых чисел является сравнительная простота процедуры. Недостатком первого подхода является то, что после генерации большого псевдопростого числа p может оказаться достаточно сложным определение разложения числа p  1, которое необходимо знать, например, в случае ЭЦП на основе сложности задачи дискретного логарифмирования с сокращенной длиной подписи. Разложение числа p  1 представляет интерес также и для отсеивания некоторых классов слабых простых чисел. Следующие два вероятностных теста могут быть применены совместно. Пусть мы хотим проверить, является ли число p простым.

• Тест Ферма заключается в проверке соотношения b p  1 = 1 (mod p) для большого числа различных значений b. Число различных использованных при тестировании значений b, для которых выполняется указанное соотношение, определяет число выполненных опытов по тесту Ферма. Однако известен класс составных чисел, которые проходят тест Ферма (числа Кармайкла). Примеры чисел из этого класса приведены в таблице 10.1.

• Тест Соловея-Штрассена заключается в проверке равенств , где – символ Лежандра для значений b являющихся квадратичными вычетами по модулю p, и для значений b, являющихся квадратичными невычетами по модулю p (квадратичным вычетом называется число, являющееся квадратом некоторого числа x по модулю p; т. е. для квадратичного вычета существует квадратный корень: b = x2 mod p).

Второй тест хорошо отсеивает числа Кармайкла. Вероятность того, что составное число пройдет один опыт по тесту Соловея-Штрассена, не превышает значения 0.5. Это позволяет получить оценку числа опытов, которые следует выполнить в соответствии с данным тестом, чтобы получить необходимо низкую вероятность принять составное число в качестве псевдопростого. Первый тест используется в качестве предварительной отбраковки чисел. Второму тесту подвергают только числа, прошедшие первый. (Второй тест на самом деле поглощает пер-вый, поскольку проверка условия = 1 для значений b, являющихся квадратичными вычетами, фактиче-ски означает проверку по тесту Ферма.)

Практическая часть

Согласно поставленной теории, была создана демонстрационная программа на языке Python, способная для случайного числа установить является ли число псевдопростым.

Программа сгенерировала массив из 200 значений b, которые используются в тестах и 20 значений числа p. Каждая строчка – результат расчетов для каждого числа. Процент показывает отношение количества удачных тестов по отношению к общему количеству тестов (200).

Число	Тест Ферма	Тест Соловея-Штрассена
282	0%	0%
424	0%	0%
534	1%	1%
594	0%	1%
115	3%	1%
773	100%	100%
247	16%	9%
401	100%	100%
598	0%	1%
193	100%	100%
779	1%	1%
441	1%	1%
291	2%	0%
484	0%	0%
150	1%	2%
438	0%	0%
753	1%	1%
895	1%	1%
523	100%	100%
875	1%	1%

Мы видим, что из случайно выбранных чисел выделяются 773, 401, 193, 523. Эти числа действительно являются простыми числами.

Листинг программы, написанный в процессе изучения генерации псевдо простых чисел.

import random def pherma(p_int, b_arr): pherma_yes = 0 for i in b_arr: if i**(p_int-1)%p_int == 1: pherma_yes += 1 return pherma_yes/len(b_arr) def solovey(p_int, b_arr): solovey_yes = 0 for i in b_arr: deg = int((p_int - 1) / 2) if i ** deg % p_int == 1 or i ** deg % p_int == p_int - 1: solovey_yes += 1 return solovey_yes/len(b_arr) if __name__ == "__main__": n_of_tests = 200 b = [random.randint(10,1000) for _ in range(n_of_tests)] print("Число\tТест Ферма\tТест Соловея-Штрассена") for i in range(20): p = random.randint(100, 1000) print("{}\t{}\t{}".format(p, pherma(p, b), solovey(p,b)))

Санкт-Петербург

2019