Итоговый тест
.pdf
15.11.2020 |
Итоговый тест |
Личный кабинет / |
Мои курсы / ВМТ - 3 и 4 семестры / |
Блок контроля освоения курса / Итоговый тест |
||
Вопрос 1 |
Решите дифференциальное уравнение x y’ ln(y/x) = x + y ln(y/x). Выберите пропущенную в ответе функцию из |
|||
Пока нет |
предложенных ниже. |
|
||
ответа |
ln x – |
|
(ln( y/x) - 1) = C |
|
Балл: 1,00 |
y/x |
|
||
|
|
|
|
|
ln |x| |
|
ln |y| |
|
ln |x + y| |
|
cos (y/x) |
|
e–y/x |
|
ey/x |
Определите тип дифференциального уравнения первого порядка
y’ = y/x + y2ex
линейное уравнение
Вопрос 3 |
Решите дифференциальное уравнение y(x2+1) y’ + x(1 + y2)= 0. Выберите пропущенную в ответе функцию из |
|||
Пока нет |
предложенных ниже. |
|||
ответа |
( |
x2 |
+ 1)(1 + y2) = C |
|
Балл: 1,00 |
||||
|
|
|
||
y2 |
|
arctg x |
|
cos x |
|
cos y |
|
sin x |
|
sin y |
|
x |
Найдите общее решение дифференциального уравнения y’’ – 2y’ + y = 0 из перечисленных ниже:
Балл: 1,00 |
|
y = C1 e x + C2 xex |
|
|
|
||
|
|
|
y = C1 e x + C2 e–x |
|
|
|
|
|
y = C1 e–2x + C2 xe–2x |
|
y = C1 ex cos x + C2 ex sin x |
|
|
|
y = C1 e–x cos x + C2 e–x sin x |
|
y = C1 + C2 e–4x |
|
|
|
y = C1 e2x cos 3x + C2 e2x sin 3x |
|
y = C1 e–2x cos 3x + C2 e–2x sin 3x |
|
|
|
y = C1 cos x + C2 sin x |
|
y = C1 e2x + C2 xe2x |
Найдите уравнения интегральных кривых дифференциального уравнения (4x3 + 2xy – 1)dx + (x2 – 3y2 + 1)dy = 0 в виде F(x, y) = C. В ответе укажите значение С для кривой, проходящей через точку (1; 1).
Не забудьте сократить выражение в левой части ответа на общий множитель.
C = 1
Решите дифференциальное уравнение ydx + (2(xy)1/2 – x)dy = 0. Выберите пропущенную в ответе функцию из предложенных ниже.
Балл: 1,00 |
(x/y)1/2 |
+ |
|
ln |y| |
= C |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |x| |
|
|
ln |x + y| |
|
y/x |
|
cos (y/x) |
|
e–y/x |
|
ey/x |
||
https://lms.spbstu.ru/mod/quiz/attempt.php?attempt=874787&cmid=18284 |
1/5 |
15.11.2020
Вопрос 7
Пока нет ответа
Балл: 1,00
Вопрос 8
Пока нет ответа
Балл: 1,00
Вопрос 9
Пока нет ответа
Балл: 1,00
Вопрос 10
Пока нет ответа
Балл: 1,00
Вопрос 11
Пока нет ответа
Балл: 1,00
Итоговый тест
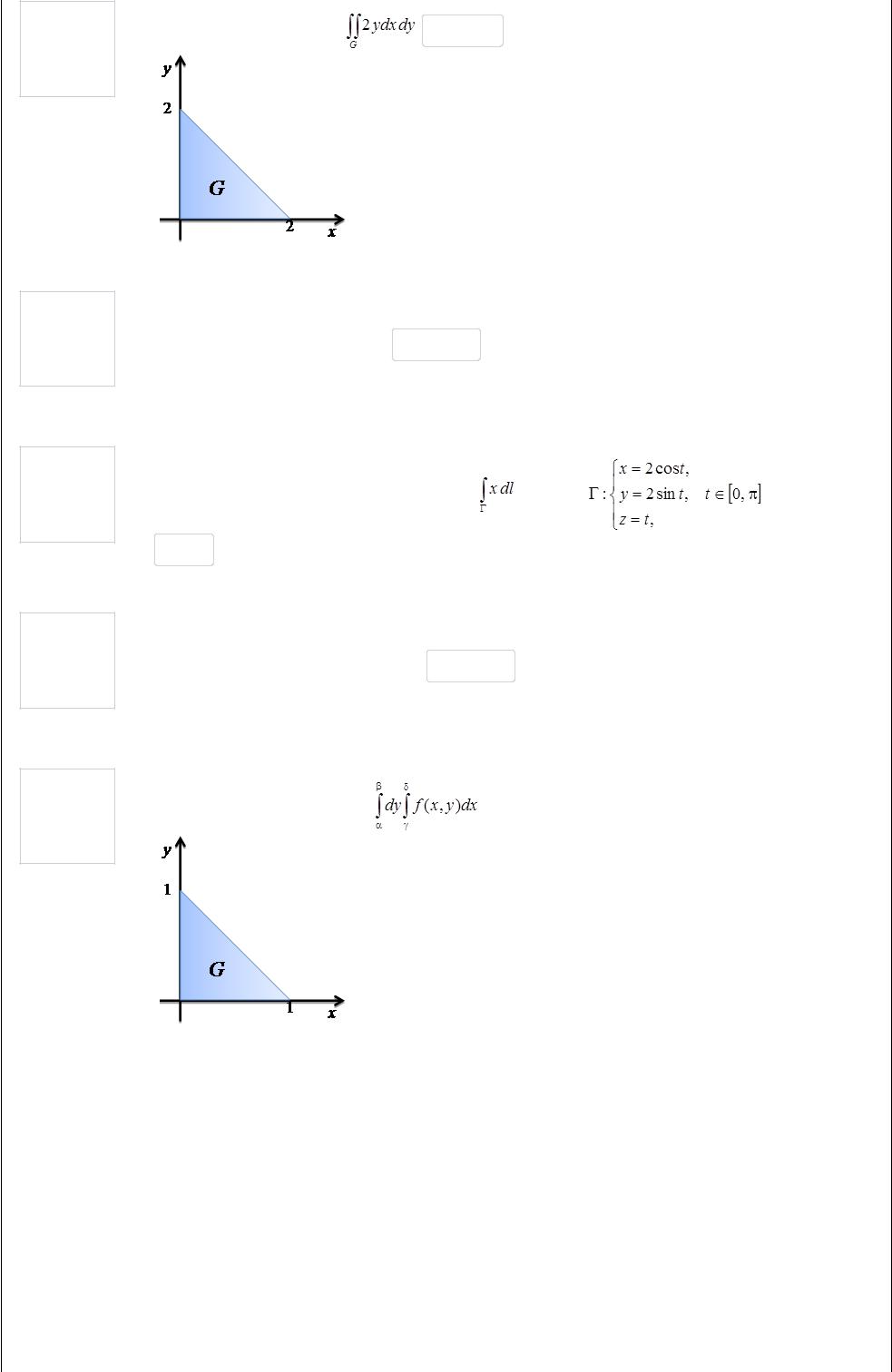
Вычислите двойной интеграл |
2.666 |
Найдите объем тела, ограниченного поверхностями, заданными уравнениями x2 + y2 = 4, x2 + y2 = z2, z = 0, z ≥ 0 ответ: 16.755
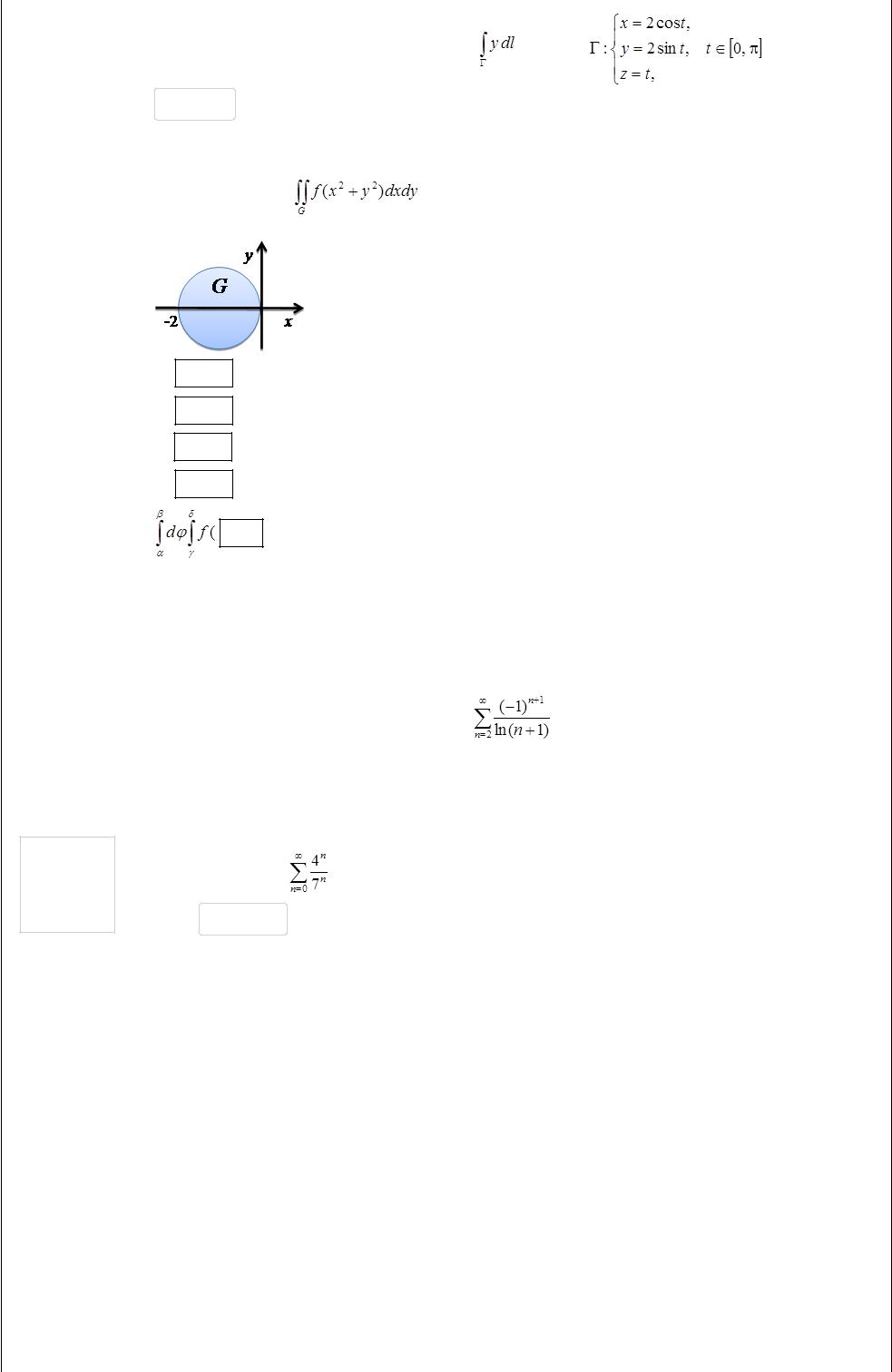
Вычислите криволинейный интеграл первого рода |
по кривой |
Ответ: |
0 |
|
|
Найдите объем тела, ограниченного поверхностями, заданными уравнениями
z = x2 + y2 + 6, z = x2 + y2 + 2, x2 + y2 = 1 ответ: 12.56
Перейдите от двойного интеграла |
к повторному, если область G изображена на рисунке. |
Введите пределы интегрирования
α = |
0 |
|
|
|
|
β = |
1 |
|
|
|
|
γ = |
0 |
|
|
|
|
δ = |
1 – y |
|
|
https://lms.spbstu.ru/mod/quiz/attempt.php?attempt=874787&cmid=18284 |
2/5 |
15.11.2020 |
|
Итоговый тест |
|
|
|
|
|
|
|
|
Вопрос 12 |
|
|
|
|
Пока нет |
Вычислите криволинейный интеграл первого рода |
по кривой |
Ответ: |
|
ответа |
|||
|
|
|
|
|
|
Балл: 1,00 |
|
|
|
|
|
8.94 |
|
|
|
|
|
|
Вопрос 13 |
В двойном интеграле |
сделайте замену переменных, перейдя к полярной системе |
|
Пока нет |
|||
|
|
||
ответа |
координат. Вставьте пропущенное |
|
|
|
|
||
Балл: 1,00 |
|
|
|
|
|
|
α = |
π/2 |
β = |
3π/2 |
γ = |
0 |
δ = –2cosφ
r2 |
)rdr |
tg φ |
|
|
r |
|
|
ctg φ |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2π |
|
|
π |
|
–2sinφ |
|
cosφ |
|
2sinφ |
|
2cosφ |
|
–π/2 |
||
Вопрос 14 |
Исследуйте на сходимость знакопеременный ряд |
. |
||
Пока нет |
||||
ответа |
|
|
|
|
Балл: 1,00 |
|
|
|
|
Ответ: |
сходится условно |
|
|
|
|
|
|
|
|
|
|
|
|
|
Вопрос 15 |
Найдите сумму ряда |
Пока нет |
|
ответа |
|
Балл: 1,00 |
Ответ: 2.333 |
https://lms.spbstu.ru/mod/quiz/attempt.php?attempt=874787&cmid=18284 |
3/5 |
15.11.2020
Вопрос 16
Пока нет ответа
Балл: 1,00
Вопрос 17
Пока нет ответа
Балл: 1,00
Вопрос 18
Пока нет ответа
Балл: 1,00
Вопрос 19
Пока нет ответа
Балл: 1,00
Итоговый тест
Разложите функцию sin x2 в ряд по степеням х.
Выберите один ответ:
Из перечисленных обобщенных гармонических рядов выберите все расходящиеся
Выберите один или несколько ответов:
Исследуйте ряд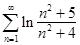 
с помощью признака сравнения. Сравните его с обобщенным гармоническим
рядом . В ответе укажите число p и сделайте вывод о сходимости (расходимости) исходного ряда.
p = 2
Исходный ряд сходится
Найдите интервал сходимости степенного ряда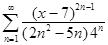 
В ответе укажите границы интервала (a; b)
a = 5
b = 9
https://lms.spbstu.ru/mod/quiz/attempt.php?attempt=874787&cmid=18284 |
4/5 |
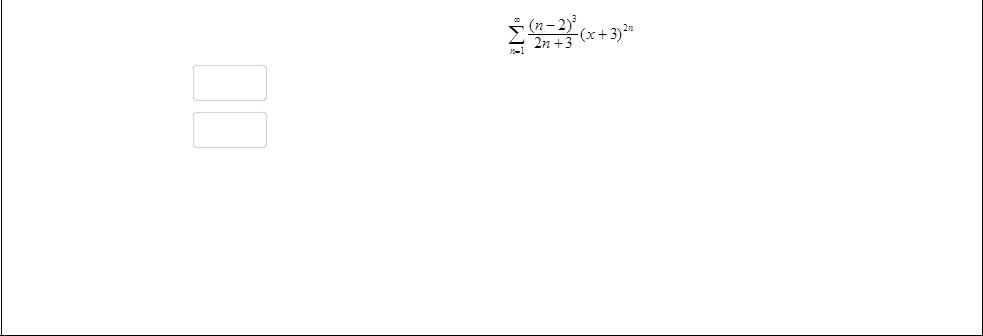
15.11.2020 |
|
|
|
Итоговый тест |
|
|
|
|
|
|
Вопрос 20 |
Найдите интервал сходимости степенного ряда |
В ответе укажите границы интервала (a; b) |
|
|
Пока нет |
|||
|
|
|
|
|
|
ответа |
|
|
|
|
Балл: 1,00 |
a = |
-4 |
|
|
|
b = |
-2 |
|
|
|
|
||
◄ Приложения степенных рядов |
Перейти на... |
ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ |
|
Лапласа ► |
|
|
|
|
|
|
https://lms.spbstu.ru/mod/quiz/attempt.php?attempt=874787&cmid=18284 |
5/5 |