10 модуль / 10_2
.pdf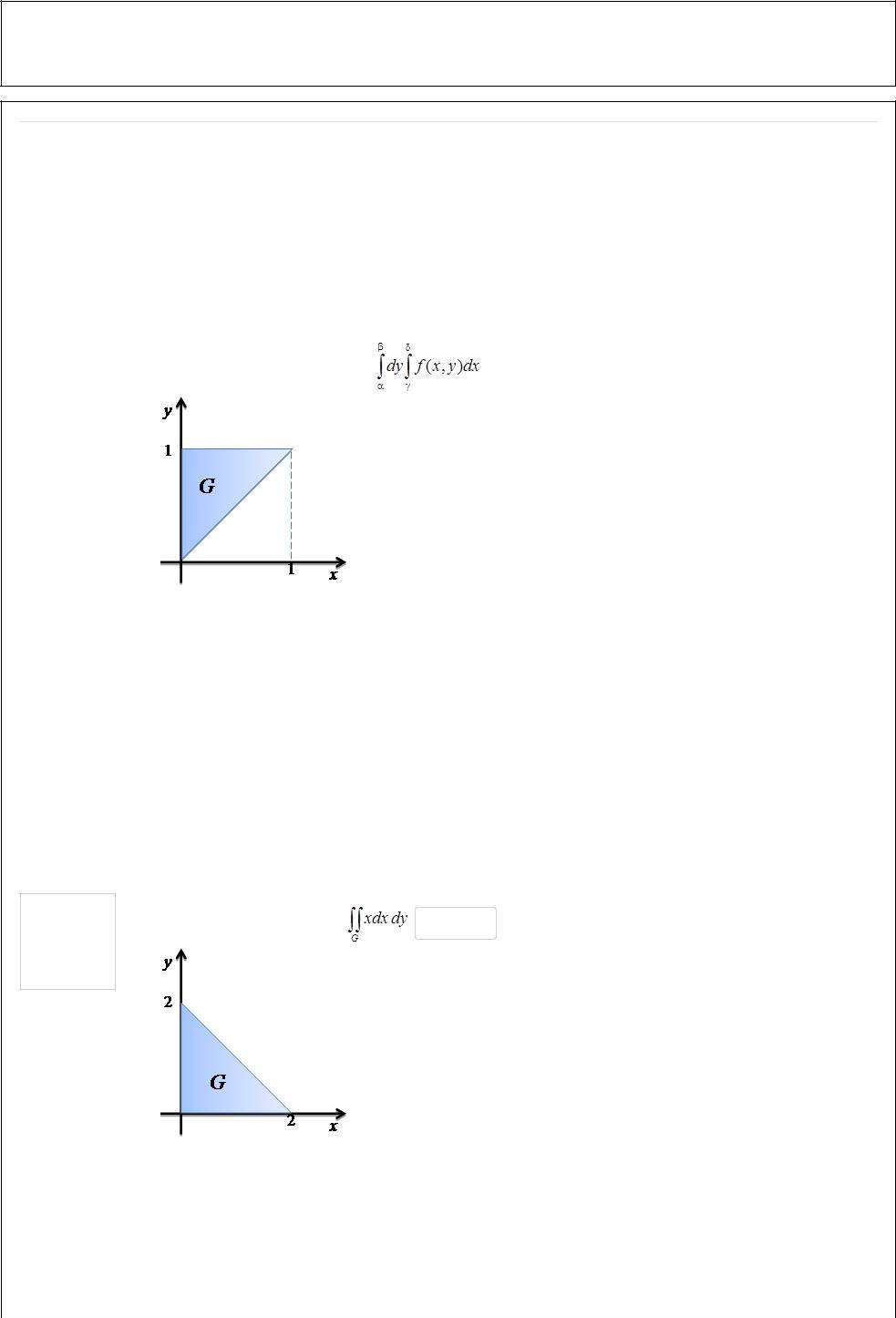
08.11.2020 |
Тест по разделу 10 |
Личный кабинет / Мои курсы / ВМТ - 3 и 4 семестры / Раздел 10. Интегральное исчиcление функций нескольких переменных / Тест по разделу 10
Тест начат |
Воскресенье, 8 ноября 2020, 14:30 |
|
|
Состояние |
Завершенные |
|
|
Завершен |
Воскресенье, 8 ноября 2020, 15:02 |
|
|
Прошло |
32 мин. 30 сек. |
|
|
времени |
|
|
|
Баллы |
2,10/7,00 |
|
|
Оценка |
6,00 из 20,00 (30%) |
|
|
Отзыв |
Тест не засчитан. Вы набрали менее 60% правильных ответов. |
||
|
|
|
|
Вопрос 1 |
|
Перейдите от двойного интеграла |
к повторному, если область G изображена на рисунке. |
Верно |
|
||
Баллов: 0,50 из |
|
|
|
1,00 |
|
|
|
|
|
|
|
Введите пределы интегрирования
α = |
0 |
|
|
|
|
|
|
|
β = |
1 |
|
|
|
|
|
|
|
γ = |
0 |
|
|
|
|
|
|
|
δ = |
y |
|
|
|
|
Верно
Оценка за этот ответ: 1,00/1,00. С учетом предыдущих попыток это дает 0,50/1,00.
Вопрос 2
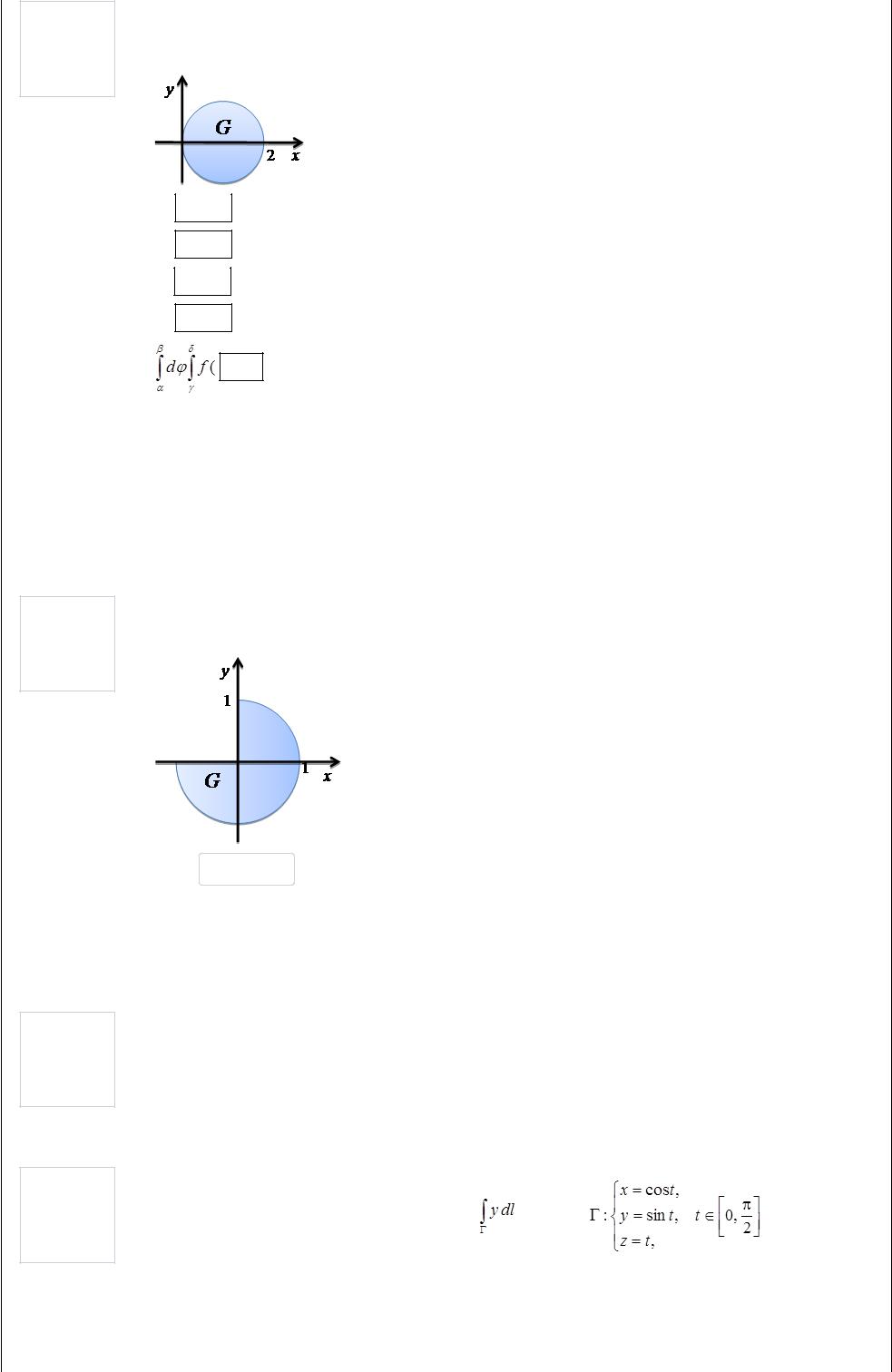
Вычислите двойной интеграл |
4 |
|
Неверно |
|
|
Баллов: 0,00 из
1,00
Неверно
Баллы за эту попытку: 0,00/1,00.
https://lms.spbstu.ru/mod/quiz/review.php?attempt=868394&cmid=18282 |
1/3 |
08.11.2020 |
Тест по разделу 10 |
Вопрос 3
Верно
Баллов: 0,60 из
1,00
Вопрос 4
Верно
Баллов: 1,00 из
1,00
Вопрос 5
Нет ответа
Баллов: 0,00 из
1,00
Вопрос 6
Нет ответа
Баллов: 0,00 из
1,00
В двойном интеграле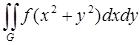 
сделайте замену переменных, перейдя к полярной системе координат. Вставьте пропущенное
α = |
–π/2 |
|
β = |
π/2 |
|
γ = |
0 |
|
δ = |
2cosφ |
|
r2 |
)rdr |
ctg φ |
|
|
tg φ |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2cosφ |
|
|
–2sinφ |
|
|
2sinφ |
|
–2cosφ |
|
2π |
|
π |
|
0 |
|
π/2 |
|
3π/2 |
|
cosφ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
–π/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Верно
Оценка за этот ответ: 1,00/1,00. С учетом предыдущих попыток это дает 0,60/1,00.
Вычислите двойной интеграл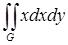 
, предварительно перейдите к полярным координатам.
Ответ: 0.333 |
|
Верно
Баллы за эту попытку: 1,00/1,00.
Найдите объем тела, ограниченного поверхностями, заданными уравнениями x2 + y2 = 1, x2 + y2 = z, z = 0 ответ: 
Вычислите криволинейный интеграл первого рода |
по кривой |
Ответ: |
https://lms.spbstu.ru/mod/quiz/review.php?attempt=868394&cmid=18282 |
2/3 |
08.11.2020 |
Тест по разделу 10 |
Вопрос 7 |
Найдите работу, совершаемую силой |
при перемещении материальной точки вдоль кривой Г y |
Нет ответа |
= –x2 Началом пути является точка А(-1; -1), |
|
|
||
Баллов: 0,00 из |
конец пути – точка В(1; -1) Ответ: |
|
1,00 |
|
|
|
|
|
◄ Вопросы и задачи для самоконтроля к |
Перейти на... |
Рекомендуемая литература ► |
главе 1 |
|
|
|
|
|
|
|
https://lms.spbstu.ru/mod/quiz/review.php?attempt=868394&cmid=18282 |
3/3 |