Билеты по электричеству и магнетизму

1. Электрический заряд. Модель точечного заряда. Инвариантность заряда. Закон сохранения заряда.

Электрический заряд – физическая величина, характеризующая свойство элементарных частиц вступать в электромагнитные силовые взаимодействия.

Единица измерения: 1 Кл (Кулон) Свойства электрического заряда:

1) Дискретность – любой электрический заряд кратен по величине элементарному заряду

( 1.6 × 10−19Кл)

Электрон – бесструктурная частица массой 9.1 × 10−31кг.

Протон – частица массой 1.67 × 10−27кг, обладающая внутренней структурой (состоит из трех кварков).

Кварки имеют дробный заряд (± 13 и ± 23 qe).

В свободном состоянии кварки не обнаруживаются, так как в объективном мире нет заряда меньшего, чем у электрона.

Модель точечного заряда:

Точечный заряд – модель заряженного тела, размерами которого можно пренебречь в условиях данной конкретной задачи ввиду малости размеров тела по сравнению с расстоянием от него до точки определения поля.

2)Электрический заряд релятивистски инвариантен – величина и знак заряда не зависит от выбора системы отсчета (т.е. от скорости). Это непосредственно следует из принципа относительности и принятого способа сравнения заряда путем измерения сил, действующих на неподвижные заряды.

3)Закон сохранения электрического заряда – в любой изолированной системе алгебраическая сумма зарядов не изменяется (в т.ч. при взаимопревращениях частиц).

(уравнение

непрерывности)

2. Закон Кулона. Полевая трактовка закона. Напряженность электрического поля.

Закон Кулона, классическая формулировка:

«Два точечных заряда q1 и q2, находящиеся на расстоянии r, взаимодействуют с силами

12 = 21 = 1 2, направленными вдоль прямой, соединяющей заряды.»

2

Полевая трактовка закона Кулона:

Если пробный заряд находится в точке пространства, в которой присутствуют поля нескольких точечных зарядов: результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.

Электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.

Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда:

=

Направление вектора Е в каждой точке пространства совпадает с направлением силы, действующей на положительный заряд.

Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим. Во многих случаях для краткости это поле обозначают общим термином – электрическое поле.

Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:

Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. В соответствии с законом Кулона напряженность электростатического поля, создаваемого

точечным зарядом Q на расстоянии r от него, равна по модулю

Если Q > 0, то вектор Е направлен по радиусу от заряда, если Q < 0, то вектор Е направлен к заряду.

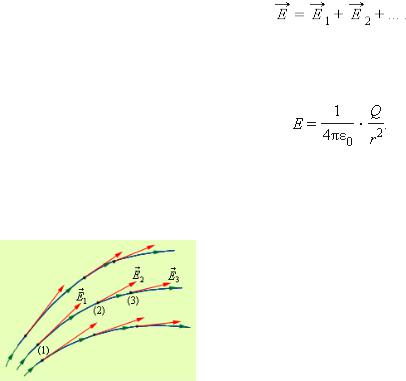
Для наглядного изображения электрического поля используют силовые линии. Эти линии проводят так, чтобы направление вектора Е в каждой точке совпадало с направлением касательной

к силовой линии. При изображении электрического поля с помощью силовых линий, их густота должна быть пропорциональна модулю вектора напряженности поля.

По принципу суперпозиции кулоновских полей точечных зарядов, изображенные на рис. поля можно рассматривать как элементарные структурные единицы («кирпичики») любого электростатического поля.

3.Электрический диполь. Дипольный момент. Поле

диполя.

Электрический диполь – система двух разноименных по знаку и одинаковых по величине точечных зарядов, находящихся на небольшом расстоянии один от другого. Вектор l, проведенный от отрицательного заряда к положительному, называется плечом диполя. Вектор =называется электрическим моментом диполя (количественная характеристика).

Напряженность поля (характеристика поля диполя), создаваемого диполем в точке, заданной радиус-вектором r, проведенным от центра диполя, (при условии l << r) приблизительно равна

4. Теорема Гаусса для электростатики (в интегральной и дифференциальной форме). Теорема Гаусса: поток вектора напряжённости электрического поля через любую,

произвольно выбранную, замкнутую поверхность равен алгебраической сумме заключённых в этой поверхности электрических зарядов, делённой на электрическую постоянная ε0.

Теорема Гаусса легко доказывается для частного случая одного точечного заряда:

Вслучае произвольного пространства распределение множества точечных зарядов используем принцип суперпозиции:

Вдифференциальной форме теорема Гаусса является локальной теоремой: дивергенция поля Е в данной точке зависит только от плотности электрического заряда r в той же точке и больше ни от чего.

Написание многих формул и действия с ними значительно упрощаются, если ввести векторный дифференциальный оператор (набла), под этим вектором подразумевается вектор с компонентами x, y, z. Следовательно, в декартовой системе координат оператор имеет вид:

5. Потенциальный характер электростатического поля. Интегральная и дифференциальная формулировки критерия потенциальности. Скалярный потенциал, разность потенциалов. Градиент потенциала. Уравнение Пуассона и Лапласа.

Работа при перемещении заряда q между двумя произвольно выбранными точками электростатического поля определяется только положением этих точек и не зависит от траектории перемещения, такие поля называются потенциальными.

Силы – центральные, поле сил – консервативное.

Интегральная и дифференциальная формулировки критерия потенциальности

«Циркуляция вектора напряженности электростатического поля по произвольному замкнутому контуру равна нулю.»

Из принципа суперпозиции следует потенциальность любого электростатического поля, созданного произвольным распределением зарядов.

Потенциал электростатического поля φ в заданной точке (r) определяется с точностью до произвольной константы.

Разность потенциалов φ между двумя точками поля определена однозначно. Нормировка потенциала на «ноль»:

- в теоретических расчетах (теория поля) φ( ) = 0

Потенциал поля нескольких точечных зарядов – на основе принципа суперпозиции:

Градиент потенциала (связь между потенциалом и напряженностью электростатического поля)

Градиент скалярной функции – вектор, направление которого совпадает наиболее быстрого возрастания функции, а модуль равен производной этой функции вдоль указанного направления.

6. Постоянное электрическое поле при наличии проводников. Электрическая емкость уединенного проводника.

Электростатическая индукция – перераспределение подвижных зарядов в проводнике под действием внешнего электростатического поля.

Поле внутри проводника В отсутствии тока, внутри проводника объемная плотность зарядов равна нулю.

Заряды могут быть только на поверхности (границе) проводящего тела. Поле вблизи поверхности проводника

Поверхность проводника – эквипотенциальна (в отсутствии тока). Электрическая емкость уединенного проводника

Потенциал проводника φ пропорционален его заряду q (экспериментальный факт):

7. Энергия электростатического поля. Энергия заряженного конденсатора. Энергия диполя во внешнем поле.

Энергия электростатического поля Поля и заряды, их образовавшие, не могут существовать обособленно. Их не разделить.

Однако переменные поля могут существовать независимо от возбуждавших их зарядов, и они переносят энергию. Эти факты заставляют признать, что носителем энергии является электростатическое поле.

При перемещении электрических зарядов силы кулоновского взаимодействия совершают определенную работу dА. Работа, совершенная системой, определяется убылью энергии взаимодействия -dW зарядов.

Электрическая энергия любой системы определяется через заряды и потенциалы: Можно определить энергию и через другие параметры электрического поля, в частности,

через напряженность E.

Рассмотрим плоский конденсатор с диэлектриком и определим его полную энергию:

Вобщем случае (для любого поля) полная энергия:

Ввыражении для энергии явным образом не входят параметры заряженных тел. Поэтому можно говорить о локализации энергии в самом электрическом поле.

Экспериментальные данные показывают, что носителем энергии является само поле.

Энергия заряженного конденсатора Для того чтобы зарядить конденсатор, нужно совершить работу по разделению

положительных и отрицательных зарядов. Согласно закону сохранения энергии эта работа равна энергии конденсатора.

Напряженность поля, созданного зарядом одной из пластин, равна Е/2, где Е — напряженность поля в конденсаторе. В однородном поле одной пластины находится

заряд q, распределенный по поверхности другой пластины. Согласно формуле Wp = qEd. Для потенциальной энергии заряда в однородном поле энергия конденсатора равна:

Так как Ed = U, где U — разность потенциалов между обкладками конденсатора, то его энергия равна:

Эта энергия равна работе, которую совершит электрическое поле при сближении пластин вплотную.

Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора, получим

Можно доказать, что эти формулы справедливы для энергии любого конденсатора, а не только для плоского.

Энергия диполя во внешнем поле

Найдем энергию, которую приобретает диполь, помещенный во внешнее электрическое поле. По определению потенциала энергия заряженной частицы во внешнем поле равна произведению ее заряда на значение потенциала в точке, где эта частица находится.

А энергия диполя:

Разложим эту функцию в ряд по малому парамтеру l с точностью до 2-го порядка малости:

Таким образом, энергия диполя во внешнем электрическом поле: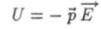

8. Постоянное электрическое поле при наличии диэлектрика. Поляризация диэлектрика. Диэлектрическая восприимчивость и диэлектрическая постоянная.

Постоянное электрическое поле при наличии диэлектрика В идеальном диэлектрике свободных зарядов, то есть способных перемещаться на

значительные расстояния (превосходящие расстояния между атомами), нет. Но это не значит, что диэлектрик, помещенный в электростатическое поле, не реагирует на него, что в нем ничего не происходит.

Любое вещество состоит из атомов, образованных положительными ядрами и отрицательными электронами. Поэтому в диэлектриках происходит поляризация.

Смещение электрических зарядов вещества под действием электрического поля называется поляризацией.

Поляризация диэлектрика

Поляризация – появление в веществе некомпенсированных поляризационных зарядов и индуцированного дипольного момента.

Диэлектрическая восприимчивость и диэлектрическая постоянная Степень поляризации характеризуется дипольным моментом единицы объема диэлектрика:

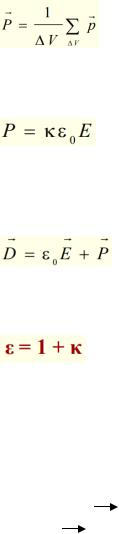
- вектор поляризации (поляризованность)

Для изотропных (поляризация всех молекул одинакова, у анизотропных – поляризация, и следовательно, вектор поляризации в разных направлениях разные.) диэлектриков:

(κ – диэлектрическая восприимчивость)

(Если внести в однородное электрическое поле диэлектрик, то поле возникших связанных зарядов будет направлено противоположно внешнему полю и ослабляет его.)

Введем вспомогательную величину, источником которой являются только сторонние заряды:

- вектор электрического смещения (электрической индукции)

Распишем Р: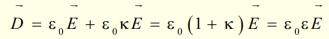

– диэлектрическая проницаемость среды: число, показывающее, во сколько раз напряженность поля в вакууме больше напряженности поля в однородном

диэлектрике.

9. Объемные и поверхностные поляризационные заряды в диэлектрике. Вектор электрического смещения. Теорема Гаусса при наличии диэлектрика. Граничные условия для вектора напряженности и смещения.

Объемные и поверхностные поляризационные заряды в диэлектрике

Положительный заряд, который пересечет поверхность dS при поляризации:

Объемные поляризационные заряды возникают только если вектор поляризации изменяется от точки к точке.

Следствие: на границе раздела двух различных диэлектриков в электрическом поле всегда возникают поляризационные поверхностные заряды.

Определим поверхностную плотность поляризационных зарядов σпол. Заряд внутри выделенного объема:

Вектор электрического смещения Для описания поля в диэлектрике удобно ввести еще одну величину – вектор электрического

смещения.

По теореме Гаусса, в поляризованном диэлектрике

-объемная плотность всех зарядов

-объемная плотность сторонних (свободных) зарядов

-объемная плотность поляризационных (связанных) зарядов

-вектор электрического смещения (вектор электрической индукции), так же зависит от свойств вещества.

Теорема Гаусса для диэлектрика

Винтегральной форме:

-описывает поле только сторонних (свободных) зарядов

-силовая характеристика поля всех (сторонних и поляризационных) зарядов

10. Молекулярная картина поляризации диэлектриков. Электронная, ионная и дипольная поляризации. Формула Клазиуса-Мосотти. Формула Дебая-Ланжевена.

Молекулярная картина поляризации диэлектриков Диэлектрики: полярные и неполярные.

Неполярные: симметричное распределение положительных и отрицательных зарядов (H2, CO2, CH4).

- индуцированный (полем) дипольный момент.

Полярные: несимметричное распределение зарядов (CO, N2O, SO2). - средний (по направлению) дипольный момент.

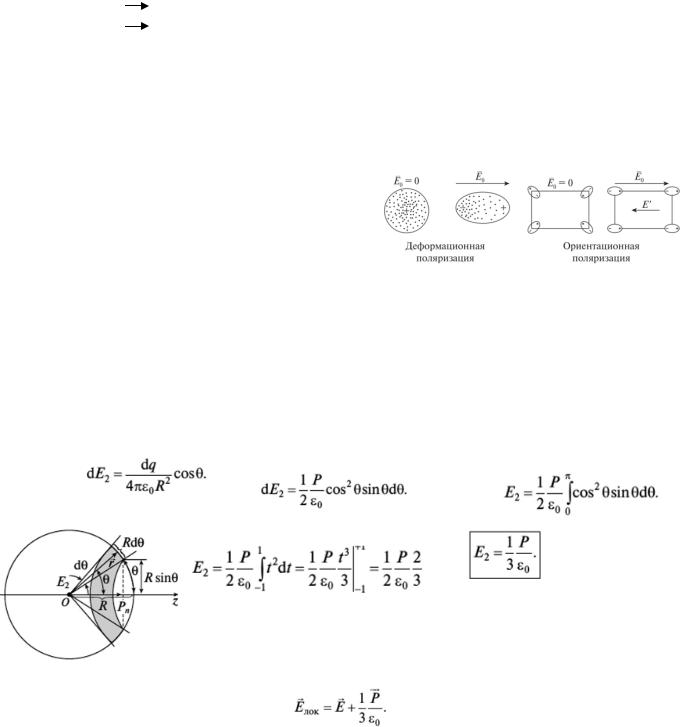
Электронная, ионная и дипольная поляризации Основные типы поляризации: деформационная и ориентационная.

Деформационная поляризация:

1)Электронная поляризация: смещение против поля электронных оболочек атомов. В линейном приближении, индуцированный дипольный момент атома:

2)Атомная поляризация: относительное смещение в молекулах (под действием поля) атомов разных типов.

3)Ионная поляризация: в твердых диэлектриках с ионными связями в кристаллической решетке (Na+Cl -)

Ориентационная (дипольная) поляризация: При отсутствии внешнего поля их дипольные

моменты ориентированы произвольным образом (изза тепловых движений). Под действием же внешнего поля дипольные моменты ориентируются преимущественно в направлении внешнего поля.

Формула Клазиуса-Мосотти. Формула Дебая-Ланжевена. Локальное поле в диэлеткрике:

Выделим на поверхности сферы Лоренца тонкое кольцо (сферический пояс) шириной AdO и с осевым (кольцевым) радиусом A sin 0. В пределах этого кольца поверхностную плотность заряда можно считать неизменной и равной Acos 0. Тогда заряд dq, распределенный по кольцу, найдем умножив площадь шарового пояса (dA = 2 л A2 sin 0d0) на поверхностную плотность заряда, т.е. d q = а' - 2 л A2 sin 0d0 = Acos 0 2лА2 sin 0d0. Этот заряд с учетом пространственного распределения создает в точке О напряженность поля

Напомним, что такая напряженность будет во всех точках внутри полости — поле ее полости однородно.

Таким образом, приближенное значение локального поля можно

записать в виде:

Применив теперь эту формулу для расчета поляризации диэлектрика .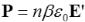

Где n - концентрация молекул диэлектрика, 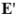- напряженность электрического поля, действующего на молекулу.

Поле 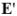создается всеми зарядами, за исключением зарядов самой молекулы, на которую оно действует. Среднее наблюдаемое поле создается всеми зарядами без исключения. Внутреннее поле относительно просто выразить для кристаллов с кубической решеткой:

В неполярных жидкостях и газах молекулы расположены хаотически – формула для внутреннего поля справедлива лишь приближенно.

Подставим и из полученного уравнения выразим P:

диэлектрике: Получим

Последнее уравнение должно выполняться тождественно для любых значений 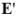, поэтому

откуда после преобразований получаем формулу Клаузиуса-Мосотти:

Равенство показывает, что для неполярных диэлектриков величина 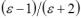прямо пропорциональна концентрации молекул, то есть – плотности вещества. При неизменной концентрации молекул диэлектрическая проницаемость не зависит от температуры, так как

поляризуемость молекул 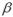зависит лишь от строения молекул, но не зависит от температуры.

Она справедлива только для неполярных диэлектриков. Ланжевен и Дебай обобщили её на случай полярных диэлектриков, в которых проявляется как электронная, так и ориентационная поляризация. Соответствующее выражение, носящее название формула Ланжевена-Дебая с учетом имеет вид:

11. Сегнетоэлектрики и пьезоэлектрики. Прямой и обратный пьезоэлектрический эффект.

Сегнетоэлектрики и пьезоэлектрики Сегнетоэлектрики – твердые полярные диэлектрики, обладающие спонтанной поляризацией (в

определенном интервале температур)

При Eвнеш = 0

Феноменологические особенности (основные свойства) сегнетоэлектриков:

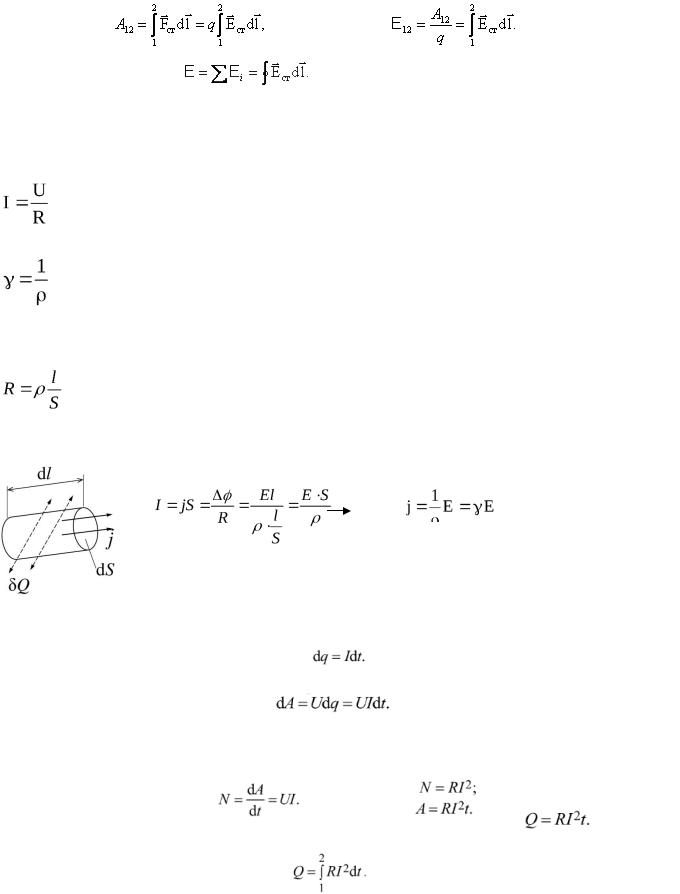
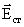– напряженность поля сторонних сил. Работа сторонних сил на участке 1 – 2:

Для замкнутой цепи:

13. Законы Ома и Джоуля-Ленца в дифференциальной и интегральной формах. Сила тока, протекающего по однородному проводнику, пропорциональна разности

потенциалов на его концах (напряжению).

- закон Ома в интегральной форме

Где R – электрическое сопротивление проводника [Ом]

- проводимость (обратная величина от сопротивления) [См] (Сименс)

R зависит от формы, размеров и материала проводника, от температуры, от распределения тока по проводнику.

В простейшем случае однородного проводника с постоянным сечением: S - сечение

l - длина проводника

Дифференциальная формулировака закона Ома

Модель: однородный изотропный проводник, в каждой точке которого j (плотность тока) || E

- закон Ома в дифференциальной

Закон Джоуля-Ленца в интегральной форме Рассмотрим произвольный участок цепи, к концам которого приложено

напряжение U. За время dt через каждое сечение проводника проходит заряд

При этом работа силы электрического поля на данном участке

Разделив работу на время, получим выражение для мощности

При протекании тока в проводнике выделяется количество теплоты

Закон Джоуля-Ленца в дифференциальной форме

Интегральная форма относится ко всему проводнику с сопротивлением R, по которому течет ток I. Получим закон в локально-дифференциальной форме, характеризуя тепловыделение в произвольной точке.