Федеральное агентство связи ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М. А. БОНЧ-БРУЕВИЧА» (СПбГУТ)

Факультет инфокоммуникационных сетей и систем Кафедра программной инженерии и вычислительной техники

ЛАБОРАТОРНАЯ РАБОТА №2 по дисциплине «Логическое и функциональное программирование»

Выполнил: студент 3-го курса дневного отделения группы ИКПИ-85

Коваленко Леонид Александрович Преподаватель:

доцент кафедры ПИиВТ Ерофеев Сергей Анатольевич

Санкт-Петербург

2020

Постановка задачи

Написать программу на языке Turbo Prolog 2.0 для построения натурального кубического сплайна.

Схема решения Приведем пример построения кубического сплайна на основе трех

точек (x1 , y1) , (x2 , y2) , (x3 , y3) .

1. Определим число отрезков.

Очевидна зависимость: Число отрезков = Число точек – 1. Число отрезков для трех точек — 2 (от x1 до x2 и от x2 до x3 ). 2. Определим число сплайнов.

Так как отрезков 2, то:

Нам предстоит найти коэффициенты a1 ,b1 ,c1 ,d1 ,a2 , b2 ,c2 , d2 .

3. Формируем систему уравнений, которая имеет следующие строки:

1) Строки кубических полиномов (по абсциссам), приравненных значениям соответствующих ординат.

a1 x31 +b1 x21+c1 x1 +d1= y1

a1 x32 +b1 x22+c1 x2 +d1= y2 a2 x32 +b2 x22+c2 x2 +d2= y2 a2 x33 +b2 x23 +c2 x3 +d2= y3

2) Строки с приравненными значениями первых производных двух полиномов в общей точке.

3a1 x22+2b1 x2+c1=3 a2 x22 +2 b2 x2+c2

3)Строки с приравненными значениями вторых производных двух

полиномов в общей точке.

6a1 x2 +2b1=6 a2 x2 +2 b2

4)Строки с приравненными нулю вторыми производными в граничных

точках. (В нашем случае — граничные точки (x1 , y1) , (x3 , y3) ).

6a1 x1 +2 b1=0

6a2 x3 +2 b2=0

Данные граничные условия нужны именно для натурального сплайна. 2

По итогу получим следующее:

Зависимость числа строк R в системе уравнений от числа точек P :

R=4 P−4

4. Решаем систему уравнений методом Гаусса.

Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Онлайн калькулятор метода Гаусса.

Код программы Входные данные поступают с клавиатуры либо файла, пример

содержимого которого приведен в табл. 1. Таблица 1 — Пример входных данных в файле

point(2,2)

point(1,1)

point(3,3)

Последовательность ввода точек (и с клавиатуры, и с файла) не имеет значения, они будут отсортированы по возрастанию координаты X . Точки с повторяющимися значениями X после сортировки будут удалены (кроме первой).

Код программы построения кубического сплайна приведен в табл. 2.

3

Таблица 2 — Код программы построения кубического сплайна

NOWARNINGS

%Раздел описания доменов

DOMAINS

file = datafile % Файл datafile

point = point(real, real) % Структура, описывающая точку points = point* % Список точек

list_of_real = real* % Список вещественных чисел

matrix = list_of_real* % Список списков вещественных чисел

%Раздел описания предикатов

PREDICATES

length(points, integer) input(points) input_action(points, integer) read_points_from_console(points) read_points_from_file(points) quicksort(points, points)

partition(points, real, points, points) merge(points, points, points) merge(list_of_real, list_of_real, list_of_real) merge(matrix, matrix, matrix)

distinct(points, points) form_system(points, matrix) create_list(real, integer, list_of_real)

create_equation(list_of_real, real, integer, integer, list_of_real) create_equation_1(point, integer, integer, list_of_real) create_equation_2(point, integer, integer, list_of_real) create_equation_3(point, integer, integer, list_of_real) create_equation_4(point, integer, integer, list_of_real) get_last(points, point)

stage_1(integer, points, matrix) stage_1_1(integer, point, list_of_real) stage_1_2(integer, points, matrix) stage_1_2(integer, points, matrix, integer) stage_1_3(integer, point, list_of_real) stage_2(integer, points, matrix) stage_2(integer, points, matrix, integer) stage_3(integer, points, matrix) stage_3(integer, points, matrix, integer) stage_4(integer, points, matrix)

gaussian_elimination_with_backsubstitution(matrix, list_of_real) gaussian_elimination(matrix, matrix, matrix) backsubstitution(matrix, list_of_real, list_of_real) backsubstitution_auxillary(list_of_real, list_of_real, real, real) pivot_row(matrix, list_of_real, matrix) normalized_pivot_row(list_of_real, list_of_real) normalized_pivot_row_auxillary(list_of_real, real, list_of_real) normalized_other_rows(matrix, list_of_real, matrix) normalized_other_row(list_of_real, real, list_of_real, list_of_real) output(points, list_of_real)

output_action(points, list_of_real, integer) write_coefficients(points, list_of_real)

%Раздел описания внутренней цели

GOAL

input(Points), % Ввод точек

quicksort(Points, SortedPoints), % Быстрая сортировка списка точек [O(N log N)] distinct(SortedPoints, SortedPointsWithoutDuplicates), % Удаление точек с повторяющимися X

[O(N)]

form_system(SortedPointsWithoutDuplicates, EquationSystem), % Формирование системы уравнений [O(N^2)]

gaussian_elimination_with_backsubstitution(EquationSystem, Result), % Решение системы

уравнений [O(N^3)]

output(SortedPointsWithoutDuplicates, Result), % Вывод результата readchar(_). % Завершение программы после нажатия клавиши клавиатуры

%Раздел описания предложений

CLAUSES

%Вспомогательные общие предикаты

%Длина списка

length([], 0). length([_|Xs], N) :-

length(Xs, P), N = P + 1.

% Ввод точек input(Points) :-

write("-== MENU ==-"), nl, write("1. Read from console;"), nl,

4

write("2. Read from file."), nl, write("Another button to exit"), nl, readint(C), % Считывание целого числа input_action(Points, C), % Ввод списка точек length(Points, Length), Length >= 3;

write("There must be at least three points!"), fail. % Если меньше 4 точек

%Ввод из диалогового окна input_action(Points, 1) :-

read_points_from_console(Points).

%Ввод из файла

input_action(Points, 2) :- write("File name: "),

readln(FileName), % Ввод названия файла existfile(FileName), % Существует ли файл openread(datafile, FileName), % Открытие файла для чтения readdevice(datafile), % Перенаправление ввода на файл read_points_from_file(Points), % Чтение точек из файла closefile(datafile), !; % Закрытие файла

write("Error reading file!"), nl, fail.

% Чтение точек с консоли read_points_from_console([point(X, Y)|Tail]) :-

write("X: "), readreal(X), % Чтение X write("Y: "), readreal(Y), % Чтение Y read_points_from_console(Tail).

read_points_from_console([]).

% Чтение точек с файла read_points_from_file([Point|Tail]) :-

readterm(point, Point), % Чтение терма point(X, Y) read_points_from_file(Tail).

read_points_from_file([]).

%Пример содержимого файла:

%point(2, 2)

%point(1, 1)

%point(3, 3)

%Быстрая сортировка

quicksort([point(X, Y)|Xs], Zs) :- partition(Xs, X, Left, Right), % Разбиение quicksort(Left, Ls), % Обработка левой части

quicksort(Right, Rs), % Обработка правой части merge(Ls, [point(X, Y)|Rs], Zs). % Объединение списков

quicksort([], []).

%Пример (для integer):

%quicksort([5, 3, 1, 2, 4], X)

%-> X = [1, 2, 3, 4, 5]

%Разбиение списка

partition([point(X, Y)|Xs], Z, Ls, [point(X, Y)|Rs]) :- X > Z,

partition(Xs, Z, Ls, Rs).

partition([point(X, Y)|Xs], Z, [point(X, Y)|Ls], Rs) :- X <= Z,

partition(Xs, Z, Ls, Rs). partition([], _, [], []).

%Примеры (для integer):

%partition([1, 2, 3, 4, 5], 2, L, X)

%-> L = [1, 2], X = [3, 4, 5]

%partition([1, 2, 3, 4, 5], 4, L, X)

%-> L = [1, 2, 3, 4], X = [5]

%Объединение двух списков

merge([H|Xs], Zs, [H|Ts]) :- merge(Xs, Zs, Ts). merge([], Zs, Zs).

%Пример (для integer):

%merge([1, 2, 3], [4, 5, 6], X)

%-> X = [1, 2, 3, 4, 5, 6]

%Удаление дубликатов точек по X [O(N) - нужна предварительная сортировка] distinct([], []). % В пустом списке нет дубликатов

distinct([Point], [Point]). % В списке из одной точки нет дубликатов distinct([point(X, Y1), point(X, _)|Tail], Result) :- % Если точки одинаковы по X

distinct([point(X, Y1)|Tail], Result).

distinct([Point1, Point2|Tail], [Point1|Result]) :- % Если точки разные по X distinct([Point2|Tail], Result).

%Пример (для integer):

%distinct([1, 1, 2, 2, 2, 3, 3, 4], X)

%-> X = [1, 2, 3, 4]

%Комментарий: без предварительной сортировки потребуется алгоритм со сложностью O(N^2)

5

% Формирование системы уравнений form_system(Points, Equations) :-

length(Points, Length),

% Строки кубических полиномов (по абсциссам), приравненных значениям соответствующих

ординат

stage_1(Length, Points, Equations1),

%Строки с приравненными значениями первых производных двух полиномов в общей точке stage_2(Length, Points, Equations2),

%Строки с приравненными значениями вторых производных двух полиномов в общей точке stage_3(Length, Points, Equations3),

%Строки с приравненными нулю вторыми производными в граничных точках

stage_4(Length, Points, Equations4),

% Объединение четырех систем уравнений merge(Equations1, Equations2, Equations12), merge(Equations3, Equations4, Equations34), merge(Equations12, Equations34, Equations).

%Создание списка длины N, заполненного значением X create_list(X, N, [X|L]) :-

N > 0, % Выполняем, пока N > 0, записывая в голову значение Х Next = N - 1, % Получаем следующее значение N

create_list(X, Next, L).

create_list(_, N, []) :- N <= 0. % Рекурсия останавливается, когда/если N меньше 1

%Создание уравнения

create_equation(List, Y, ZerosBeforeCount, ZerosAfterCount, Equation) :- create_list(0, ZerosBeforeCount, ZerosBefore), % Создание левой части уравнения create_list(0, ZerosAfterCount, ZerosAfter), % Создание правой части уравнения merge(ZerosBefore, List, EqPart1), % Слияние левой части с заполненной merge(EqPart1, ZerosAfter, EqPart2), % Последующее слияние с правой частью merge(EqPart2, [Y], Equation). % Добавление Y в конец

% Создание уравнения первого этапа

create_equation_1(point(X, Y), ZerosBeforeCount, ZerosAfterCount, Equation) :- AX = X * X * X, BX = X * X,

List = [AX, BX, X, 1], % List = [X^3, X^2, X, 1] create_equation(List, Y, ZerosBeforeCount, ZerosAfterCount, Equation).

% Создание уравнения второго этапа

create_equation_2(point(X, _), ZerosBeforeCount, ZerosAfterCount, Equation) :- AX = 3 * X * X, BX = 2 * X, NAX = -AX, NBX = -BX,

List = [AX, BX, 1, 0, NAX, NBX, -1, 0], % List = [3*X^2, 2*X, 1, 0, -3*X^2, -2*X, -1, 0] create_equation(List, 0, ZerosBeforeCount, ZerosAfterCount, Equation).

% Создание уравнения третьего этапа

create_equation_3(point(X, _), ZerosBeforeCount, ZerosAfterCount, Equation) :- AX = 6 * X, BX = 2, NAX = -AX, NBX = -BX,

List = [AX, BX, 0, 0, NAX, NBX, 0, 0], % List = [6*X, 2, 0, 0, -6*X, -2, 0, 0] create_equation(List, 0, ZerosBeforeCount, ZerosAfterCount, Equation).

% Создание уравнения четвертого этапа

create_equation_4(point(X, _), ZerosBeforeCount, ZerosAfterCount, Equation) :- AX = 6 * X, BX = 2,

List = [AX, BX, 0, 0], % List = [6*X, 2, 0, 0]

create_equation(List, 0, ZerosBeforeCount, ZerosAfterCount, Equation).

% Получение последней точки списка get_last([Head], LastPoint) :- Head = LastPoint.

get_last([_|Tail], LastPoint) :- get_last(Tail, LastPoint).

%Строки кубических полиномов (по абсциссам), приравненных значениям соответствующих ординат stage_1(Length, [Point|Tail], Equations) :-

get_last(Tail, LastPoint),

stage_1_1(Length, Point, Equation1), % Уравнение для первой точки

stage_1_2(Length, Tail, Equations2), % Уравнения для точек между первой и последней stage_1_3(Length, LastPoint, Equation3), % Уравнение для последней точки merge([Equation1], Equations2, Eq12), % Слияние уравнений

merge(Eq12, [Equation3], Equations).

%Уравнение для первой точки

stage_1_1(Length, Point, Equation) :- ZerosAfterCount = 4 * (Length - 2),

create_equation_1(Point, 0, ZerosAfterCount, Equation).

% Уравнения для точек между первой и последней

stage_1_2(Length, Tail, Equations) :- stage_1_2(Length, Tail, Equations, 1). stage_1_2(_, [_], [], _).

stage_1_2(Length, [Point|Tail], [Equation1, Equation2|Equations], CurrentIndex) :- ZerosBeforeCount1 = 4 * (CurrentIndex - 1),

ZerosAfterCount1 = 4 * (Length - CurrentIndex - 1), ZerosBeforeCount2 = 4 * CurrentIndex,

6

ZerosAfterCount2 = 4 * (Length - CurrentIndex - 2), create_equation_1(Point, ZerosBeforeCount1, ZerosAfterCount1, Equation1), create_equation_1(Point, ZerosBeforeCount2, ZerosAfterCount2, Equation2), NewCurrentIndex = CurrentIndex + 1,

stage_1_2(Length, Tail, Equations, NewCurrentIndex).

%Уравнение для последней точки stage_1_3(Length, Point, Equation) :-

ZerosBeforeCount = 4 * (Length - 2), create_equation_1(Point, ZerosBeforeCount, 0, Equation).

%Строки с приравненными значениями первых производных двух полиномов в общей точке stage_2(Length, Points, Equations) :- stage_2(Length, Points, Equations, 0). stage_2(Length, [_|Tail], Equations, 0) :- stage_2(Length, Tail, Equations, 1). stage_2(_, [_], [], N) :- not(N = 0).

stage_2(Length, [Point|Tail], [Equation|Equations], CurrentIndex) :-

ZerosBeforeCount = 4 * (CurrentIndex - 1), ZerosAfterCount = 4 * (Length - CurrentIndex - 2),

create_equation_2(Point, ZerosBeforeCount, ZerosAfterCount, Equation), NewCurrentIndex = CurrentIndex + 1,

stage_2(Length, Tail, Equations, NewCurrentIndex).

%Строки с приравненными значениями вторых производных двух полиномов в общей точке stage_3(Length, Points, Equations) :- stage_3(Length, Points, Equations, 0). stage_3(Length, [_|Tail], Equations, 0) :- stage_3(Length, Tail, Equations, 1). stage_3(_, [_], [], N) :- not(N = 0).

stage_3(Length, [Point|Tail], [Equation|Equations], CurrentIndex) :- ZerosBeforeCount = 4 * (CurrentIndex - 1),

ZerosAfterCount = 4 * (Length - CurrentIndex - 2), create_equation_3(Point, ZerosBeforeCount, ZerosAfterCount, Equation),

NewCurrentIndex = CurrentIndex + 1, stage_3(Length, Tail, Equations, NewCurrentIndex).

%Строки с приравненными нулю вторыми производными в граничных точках

stage_4(Length, [Point|Tail], [Equation1, Equation2]) :- First_ZerosAfterCount = 4 * (Length - 2), create_equation_4(Point, 0, First_ZerosAfterCount, Equation1), get_last(Tail, Last),

Last_ZerosBeforeCount = 4 * (Length - 2), create_equation_4(Last, Last_ZerosBeforeCount, 0, Equation2).

% Решение системы уравнений методом Гаусса gaussian_elimination_with_backsubstitution(Ass, Xs) :-

gaussian_elimination(Ass, [], ReversedReducedAss), % Прямой ход метода Гаусса backsubstitution(ReversedReducedAss, [], Xs). % Обратный ход метода Гаусса

%Пример:

%gaussian_elimination_with_backsubstitution([[1, 2, 3], [2, 2, 3]], X)

%-> X = [0, 1.5]

%Прямой ход метода Гаусса

gaussian_elimination([], Xss, Xss). gaussian_elimination(Lower, Upper, Xss) :-

pivot_row(Lower, PivotRow, OtherRows), % Получаем строку с опорным элементом normalized_pivot_row(PivotRow, NormalizedPivotRow), % Приводим строку с опорным

элементом к нормальному виду

normalized_other_rows(OtherRows, NormalizedPivotRow, NewLower), % Приводим другие строки

к нормальному виду

gaussian_elimination(NewLower, [NormalizedPivotRow|Upper], Xss). % Повтор

%Пример:

%gaussian_elimination([[1, 2, 3], [2, 2, 3]], [], X)

%-> X = [[(3-1*(3/2))/(2-1*(2/2))], [2/2, 3/2]] = [[1.5], [1, 1.5]]

%Получение опорного элемента

pivot_row([PivotRow], PivotRow, []). pivot_row([[X1|Row1],[X2|Row2]|Rows], PivotRow, [[X2|Row2]|Rest]) :-

abs(X1) > abs(X2), !, % Ищем максимальный по модулю элемент pivot_row([[X1|Row1]|Rows], PivotRow, Rest). % Ищем опорный элемент в первом столбце

матрицы

pivot_row([Row1,Row2|Rows], PivotRow, [Row1|Rest]) :- % Перебираем все строки pivot_row([Row2|Rows], PivotRow, Rest). % Для нахождения опорного элемента

%Приведение строки к нормальному виду normalized_pivot_row([Pivot|As], Bs) :-

not(Pivot = 0.0), % Недопускаем деления на нуль normalized_pivot_row_auxillary(As, Pivot, Bs).

%Приведение остальных строк к нормальному виду normalized_other_rows([], _, []). normalized_other_rows([[A|As]|Ass], PivotRow, [Bs|Bss]) :-

normalized_other_row(As, A, PivotRow, Bs), normalized_other_rows(Ass, PivotRow, Bss).

7

%Вспомогательный предикат для приведения строки к нормальному виду normalized_pivot_row_auxillary([], _, []). normalized_pivot_row_auxillary([A|As], Pivot, [B|Bs]) :-

B = A / Pivot, % Делим значение головы списка на значение опорного элемента normalized_pivot_row_auxillary(As, Pivot, Bs).

%Приведение строки к нормальному виду

normalized_other_row([], _, [], []). normalized_other_row([A|As], X, [P|Ps], [B|Bs]) :-

B = A - X * P, % Вычитаем строки из строки с опорным элементом normalized_other_row(As, X, Ps, Bs). % Берем следующие числа в списках

%Обратный ход метода Гаусса backsubstitution([], Xs, Xs).

backsubstitution([As|Ass], Ys, Xs) :- % Обратная подстановка backsubstitution_auxillary(Ys, As, 0, Y),

backsubstitution(Ass, [Y|Ys], Xs). % Обратная подстановка для оставшейся части

%Пример:

%backsubstitution([[1.5], [1, 1.5]], [], X)

%-> X = [1.5-(0+(1.5-0)*1), 1.5-0] = [0, 1.5]

%Вспомогательный предикат для обратного хода метода Гаусса

backsubstitution_auxillary([], [B], Acc0, Acc) :- % Ищем один неизвестный свободный член в строке

Acc = B - Acc0. % Вычитаем правую часть backsubstitution_auxillary([X|Xs], [A|As], Acc0, Acc) :-

Acc1 = Acc0 + X * A, % Подставляем предыдущие значения backsubstitution_auxillary(Xs, As, Acc1, Acc).

%Вывод результата output(Points, Result) :-

write("1. Write to console;"), nl, write("2. Write to file."), nl, write("Another button to exit"), nl, readint(C), % Считывание числа output_action(Points, Result, C); % Вывод write("The program is complete.").

%Вывод в диалоговое окно

output_action(Points, Result, 1) :- write_coefficients(Points, Result).

% Вывод в файл output_action(Points, Result, 2) :-

write("File name: "), readln(FileName), % Ввод названия файла

openwrite(datafile, FileName), % Открытие файла для записи writedevice(datafile), % Перенаправление вывода на файл write_coefficients(Points, Result), % Запись данных closefile(datafile). % Закрытие файла

% Вывод коэффициентов для каждого отрезка write_coefficients([_], []).

write_coefficients([point(X1, _), point(X2, Y2)|PointTail], [A, B, C, D|CoefTail]) :- write("From X=", X1, " To X=", X2), nl,

write("A: ", A), nl, write("B: ", B), nl, write("C: ", C), nl, write("D: ", D), nl, nl,

write_coefficients([point(X2, Y2)|PointTail], CoefTail).

Тестирование Для точек (1, 1) , (2 ,2) , (3 ,3) получим следующий результат:

a1=0 , b1=0 , c1=1 ,d1=0 , a2=0, b2 =0 ,c2=1 , d2 =0

Для точек (1, 1) , (2 ,8) , (3 ,27) получим следующий результат:

a1=3 , b1=−9 , c1=13 ,d1=−6 ,a2 =−3 ,b2=27 ,c2=−59 ,d2 =42

Для точек (−1, 0.5) , (0 , 0) , (3 ,3) получим следующий результат:

a1=0.1875 ,b1=0.5625,c1=−0.125 ,d1=0 , a2=−0.0625, b2=0.5625 ,c2=−0.125 ,d2 =0

Данные результаты совпадают с результатами онлайн сервиса.

8

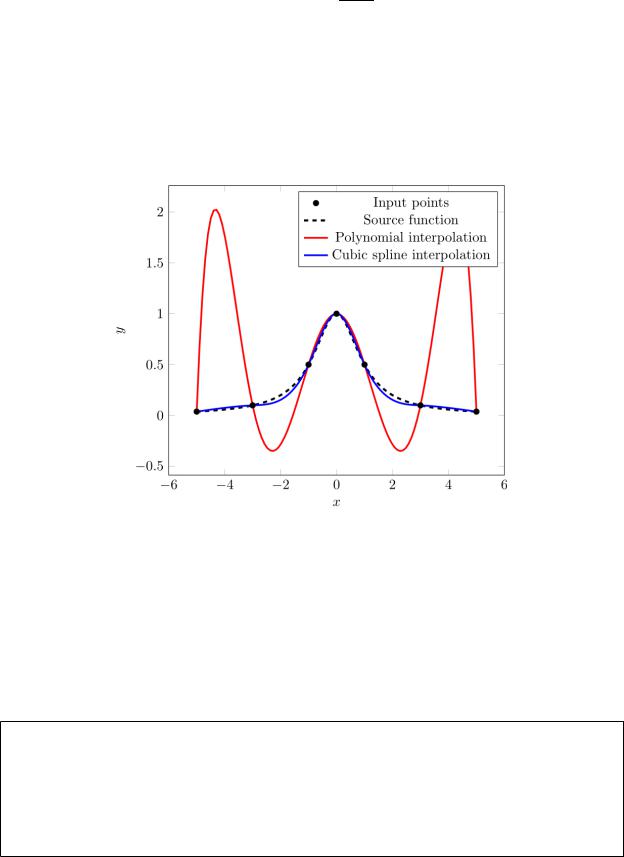
Феномен Рунге — эффект нежелательных осцилляций (колебаний), возникающий при интерполяции полиномами высоких степеней.

В качестве примера феномена Рунге обычно приводится функция:

f(x)=1+1x2

Если интерполировать её между −5 и 5 чисто полиномиально, то полученный интерполянт будет осциллировать ближе к концам интервала (с возрастанием степени полинома погрешность такой интерполяции стремится к бесконечности). Интерполяция кубическим сплайном в этом случае справляется гораздо лучше (рис. 1).

Рисунок 1 — Интерполяция кубическим сплайном и полиномиальным многочленом функции типа Рунге

Полиномиальная интерполяция была выполнена онлайн сервисом. Интерполяция кубическим сплайном выполнялась при помощи

разработанной программы и сверялась с онлайн сервисом. Входные данные приведены в табл. 3.

Таблица 3 — Входные данные с точками функции 1/(1+x2)

point(-5, 0.038461538) point(-3, 0.1) point(-1, 0.5) point(0, 1)

point(1, 0.5) point(3, 0.1) point(5, 0.038461538)

9

Результат работы программы был записан в файл (табл. 4). Таблица 4 — Файл с результатом построения кубического сплайна

From X=-5 To X=-3

A:-0.0021153846312

B:-0.031730769469

C:-0.11942307782

D:-0.029807693281

From X=-3 To X=-1

A:0.052884615406

B:0.46326923087

C:1.3655769232

D:1.4551923077

From X=-1 To X=0

A:-0.40230769232

B:-0.90230769232

C:0

D:1

From X=0 To X=1

A:0.40230769232

B:-0.90230769232

C:0

D:1

From X=1 To X=3

A:-0.052884615406

B:0.46326923087

C:-1.3655769232

D:1.4551923077

From X=3 To X=5

A:0.0021153846312

B:-0.031730769469

C:0.11942307782

D:-0.029807693281

Выводы В результате выполнения лабораторной работы мы разработали

программу на языке Turbo Prolog 2.0 для построения кубического сплайна. Было проведено тестирование отдельных предикатов и всей программы в целом. Программа полностью удовлетворяет заданным требованиям.

10