Система автоматического управления Митенков Ф.М., Чирков В.А

рого на долл ниже критического значения, скорость прироста реактивности

на случай неконтролируемой большой скорости перемещения регулирующих органов.

Из уравнения (3.74) следует, что контроль по периоду может обеспечить безопасность не только в отношении установившегося периода, но и в отношении такой скорости возрастания реактивности, которая может привести реактор к мгновенной критичности в очень короткое время.

Большие значения . При большой скорости изменения реактивности (несколько долларов в секунду и выше) плотность нейтронов существенно изменяется в интервале времени, в течение которого генерация запаздывающих нейтронов изменяется несущественно. В этом случае можно считать, что в начальный период времени

,

где индекс "0" - относится к исходному равновесному значению. Подстановка этого выражения в (3.29) приводит к уравнению (S* не учитывается):

- значение при . Уравнение (3.79) справедливо вплоть до значения ρ, соответствующего мгновенной критичности.

Для реактора, первоначально находившегося в подкритическом состоянии, можно использовать уравнения (3.77) и (3.78), отсчитывая время от момента достижения критичности, при котором

60

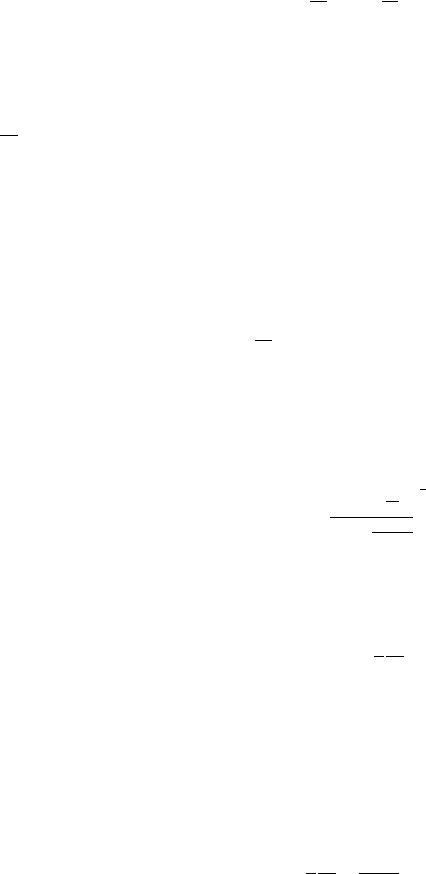
(3.80)

момент времени близка к значению, соответствующему постоянной реактивности, которая к данному моменту введена в реактор. Следовательно, период реактора должен быть близок к величине установившегося периода, определяемого соотношением (3.41) при значении реактивности, соответствующей данному моменту времени. В случае критического реактора, в котором реактивность начала изменяться в момент , справедливо приближение

(3.81)

где - начальный уровень плотности нейтронов; - установившийся обратный период, соответствующий реактивности,

имеющийся в момент времени t и

. (3.82)

Из уравнения (3.81) следует, что величина обратная периоду реактора, определяется выражением

Соотношение (3.82) можно представить в одногрупповом приближении, пренебрегая временем жизни мгновенных нейтронов, следующим образом

Тогда из уравнений (3.75) и (3.84) следует:

,

что находится в согласии с выражением (3.74).

Следовательно, и в случае малых значений скорости изменения реактивности сохраняется зависимость периода и от реактивности и от скорости ее изменения.

61

ГЛАВА IV

ОБРАТНЫЕ СВЯЗИ В РЕАКТОРЕ

§4-1. Общие сведения.

Вэнергетических реакторах изменение уровня мощности сопровождается изменением температуры ядерного топлива, замедлителя, теплоносителя, конструкционных материалов активной зоны, отражателя и т. д., а также величины отравления реактора.

Из-за этого изменяются ядерные сечения поглощения, рассеяния, деления

нейтронов и, в конечном итоге, коэффициент размножения следовательно, в реакторе существуют обратные связи.

Действительно, если в какой-то момент установившийся режим работы реактора нарушен введением извне реактивности, то в последующие моменты произойдет увеличение или уменьшение величины реактивности уже как следствие изменения режима его работы, т. е. соответствующего изменения физических параметров.

Различают внутренние и внешние обратные связи реактора. Внутренние обратные связи реализуются в результате внутриреакторных процессов. К внешним обратным связям относятся вмешательство оператора или воздействие автоматической системы регулирования, как реакция на те или иные отклонения режима работы реактора. Ниже будут рассматриваться только внутренние обратные связи.

Обратные связи в реакторе могут быть и положительные, и отрицательные. Примером положительной обратной связи в реакторе является уменьшение с ростом температуры сечения поглощения выгорающего поглотителя (например, 5B10) или материалов органов компенсации избыточной реактивности. Увеличение мощности реактора приводит к аналогичному эффекту, поскольку при этом, как правило, растет температура оставляющих элементов активной зоны реактора, включая материалы выгорающего поглотителя и органов компенсации.

Примером отрицательной обратной связи является ухудшение свойств воды как замедлителя в водо-водяных реакторах при увеличении температуры.

При изучении поведения энергетического реактора необходимо уметь определять все составляющие реактивности, обусловленные внутренними обратными связями.

Реактивность в уравнениях кинетики можно представить в виде:

внутренними процессами в данном реакторе и характером возмущения.

62

Очевидно, что в этом случае математическая модель реактора должна включать не только уравнения кинетики, но и всю совокупность уравнений, описывающих процессы, обуславливающие все обратные связи по реактивности.

Для исследования динамического поведения реактора наибольший интерес представляют температурные обратные связи (из-за их "быстродействия").

§ 4-2. Температурные обратные связи.

Под температурными обратными связями в общем случае подразумевают те изменения реактивности, которые являются следствием выделения энергии при делении ядер и последующего изменения температуры и плотности отдельных элементов активной зоны и реактора в целом. Принято температурные обратные

реакторов, поскольку изменение температуры приводит к самым разнообразным физическим и химическим эффектам (например, изменение агрегатного состояния или замедлителя, газовыделения).

Однако для гомогенного реактора температурный коэффициент реактивности может быть получен при некоторых упрощающих предположениях.

Гомогенные реакторы. Рассмотрим точечную модель гомогенного реак-

Поскольку для всех практически интересных случаев ф близко к 1, то хорошим приближением для инженерных расчетов может служить выражение

ф

63

В рассматриваемом приближении

где η - среднее число нейтронов, испускаемых при захвате одного теплового нейтрона ядрами топлива;

ε- коэффициент размножения на быстрых нейтронах;

-вероятность избежать резонансного поглощения;

-коэффициент теплового использования;

-вероятность избежать утечки для тепловых и быстрых нейтронов соот-

ветственно.

В соответствии с (3.5) и (3.6) получим

Температурный коэффициент для величины η обусловлен различной за-

Коэффициент размножения на быстрых нейтронах ε в гомогенных тепловых реакторах не зависит от температуры, поэтому температурный коэффи-

p определяется эффектом Допплера. С ростом температуры тепловое возбуждение атомов топлива приводит к уширению резонансных линий , а следовательно, и к увеличению поглощения в нем резонансных нейтронов. Однако в гомогенных тепловых реакторах концентрация топлива мала, и поэтому мал микроскопиче-

где индексы "г" и "з" относятся соответственно к топливу и замедлителю; N - ядерная плотность.

Из (3.11) следует, что

ратуры, выражение (4.12) при некоторых упрощающих посылках можно привести к виду

коэффициент реактивности приводит к следующим выражениям вместо (4.9) и

(4.10):

65

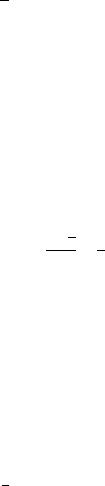
(4.14)

Здесь - температурный коэффициент объемного расширения; - константа 0.1, характеризующая температурную зависимость коэффициента

диффузии

, (4.16)

где использовано общепринятое обозначение

Если , , и малы, то , и температурный коэффициент реактивности гомогенного реактора без отражателя описывается выражением

по абсолютной величине с ростом температуры. Поскольку В2 входит в оба слагаемых в качестве множителя, можно заключить, что с уменьшением размеров гомогенного реактора при прочих равных условиях абсолютная величина ко-

реакторов с водяным замедлителем.

Гетерогенные тепловые реакторы. Для гетерогенного реактора расчет температурного коэффициента реактивности является значительно более сложной задачей, чем для гомогенного.

Это объясняется тем, что в гетерогенном реакторе увеличение температуры за счет реакции деления может быть весьма неоднородным. Известно, что основная часть тепловой энергии в активной зоне выделяется в результате торможения осколков деления, пробеги которых в твердых телах и жидкостях малы и составляют доли миллиметра. Поэтому мгновенные источники тепла, проявляющиеся практически без запаздывания, распределены, в основном, в объеме сердечников тепловыделяющих элементов. По отношению к ним температурные

66

изменения в теплоносителе, замедлителе, конструкционных материалах запаздывают и определяются нестационарными процессами теплопередачи. Для режимов работы гетерогенного реактора, сопровождающихся быстрым изменением мощности, температурный коэффициент целесообразно считать состоящим из мгновенной и запаздывающей компонент. Эффекты реактивности, зависящие от состояния топлива в данный момент времени (например, эффект Допплера, искривление тепловыделяющих элементов), могут рассматриваться как мгновенные, а эффекты, зависящие от состояния замедлителя, теплоносителя, конструкционных элементов (например, температура нейтронного газа, температурное расширение замедлителя и др.) являются в той или иной степени запаздывающими.

При исследовании очень быстрых и кратковременных изменений мощности запаздывающими эффектами можно пренебречь. В общем случае неоднородного изменения температуры в активной зоне необходимо оценивать вклады всех эффектов в изменение реактивности.

Следовательно, в случае гетерогенного реактора знания изотермического коэффициента реактивности совершенно недостаточно для исследования большинства практически важных режимов работы гетерогенных реакторов. Ниже приводится оценка составляющих изотермического коэффициента реактивности гетерогенного реактора.

Отношение микроскопических сечений в выражении для η зависит главным образом от спектра нейтронов, который определяется состоянием замедлителя. Следовательно, температурный коэффициент входит в состав запаздывающей части температурного коэффициента реактивности реактора. Как и в случае гомогенных реакторов, для всех видов топлива, кроме Pu239, коэффициент обычно мал.

Вгетерогенном реакторе коэффициент размножения на быстрых нейтронах е может изменяться с температурой по двум причинам: тепловое расширение ТВЭЛ изменяет вepoятность вылета быстрых нейтронов из топлива (этот эффект практически мгновенный; с изменением температуры топлива несколько изменяется пространственное распределение потока тепловых нейтронов в ячейке, а значит, и пространственное распределение источников быстрых нейтронов, что снова приводит к изменению вероятности вылета быстрых нейтронов из топлива. Выравнивание потока тепловых нейтронов в объеме элементарной ячейки с ростом температуры замедлителя происходит в основном за счет увеличения L2, следовательно, этот эффект изменения ε можно считать запаздывающим. Оба эффекта обычно очень малы.

Вгетерогенном реакторе с низкообогащенным топливом влияние температуры на вероятность избежать резонансного поглощения р (эффект Допплера) весьма существенно. Приближенная формула для р в гетерогенном реакторе имеет вид:

67

где - плотность ядер резонансного поглотителя в объеме топлива;

,- объемы топлива и замедлителя соответственно;

-замедляющая способность замедлителя;

-резонансный интеграл.

- линейная функция от отношения поверхности топлива к его массе.

(4.20)

Для случая быстрых изменений мощности, когда температура замедлителя не

компонентой . В случае жидкого замедлителя при изменении температуры весовое содержание его в активной зоне также изменяется. Поэтому, если

, то

где - объемный коэффициент расширения замедлителя. Следовательно

68

. (4.25)

Вытеснение замедлителя приводит к росту абсолютною значения отрицательного температурного коэффициента р, так как увеличивается отношение ядер топлива и замедлителя.

Для коэффициента теплового использования в гетерогенном реакторе справедлива формула:

где - коэффициент проигрыша, определяемый выражением

Величины с чертой - средние по объему замедлителя и топлива потеки нейтронов.

. (4.28)

Коэффициент проигрыша с увеличением Т уменьшается, поскольку пространственное распределение потока нейтронов выравнивается, что происходит в основном за счет увеличения L2 замедлителя при нагреве и является поэтому запаздывающим эффектом.

В предыдущем выражении можно считать, как и ранее, . В случае очень быстрых изменений все остальные члены в (4.28) также малы. Следовательно, в этом случае . При изменении мощности (длительном, быстром или достаточно медленном) замедлитель нагревается, что приводит к

Для жидкого замедлителя с фиксированным объемом з, учитывая (4.24), получим

очень сложен, и знак его всегда отрицателен (увеличение Т приводит к выравни-

69