Дискретная математика

DLQ TOJ VE FUNKCII f . tEOREMA O MINIMALXNOJ dnf. mINIMALXNAQ dnf SOSTOIT

TOLXKO IZ PROSTYH KON_@NKTOW.

dOKAZATELXSTWO. pUSTX K1 _ K2 _ : : : _ Ks MINIMALXNAQ dnf FUNKCII f . eSLI BY, NAPRIMER, KON_@NKT K1 NE BYL PROSTYM, TO UDALENIEM SOMNOVITELEJ IZ NEGO MOVNO BYLO BY POLU^ITX PROSTOJ KON_@NKT K10 . tOGDA K10 _K2_: : :_Ks { dnf FUNKCII f , IME@]AQ MENX[EE ^ISLO BUKW, ^TO PROTIWORE^IT MINIMALXNOSTI ISHODNOJ dnf. tEOREMA DOKAZANA.

oPREDELENIE 3. sOKRA]ENNOJ dnf FUNKCII f NAZYWAETSQ DIZ_@NKCIQ WSEH EE PROSTYH KON_@NKTOW.

tEOREMA O SOKRA]ENNOJ dnf. l@BAQ BULEWA FUNKCIQ f , NE RAWNAQ TOVDESTWENNO NUL@, RAWNA SWOEJ SOKRA]ENNOJ dnf.

dOKAZATELXSTWO. pUSTX P1; P2; : : : ; Pk WSE PROSTYE KON_@NKTY

FUNKCII f . dOKAVEM RAWENSTWO f(x1; : : : ; xn) = P1(x1; : : : ; xn)_ _P2(x1; : : : ; xn) _ : : : _ Pk(x1; : : : ; xn) . rASSMOTRIM PROIZWOLXNYJ NABOR (a1 ; : : : ; an) I RAZBEREM 2 SLU^AQ.

1) f(a1; : : : ; an) = 0 , TOGDA WSE Pi(a1; : : : ; an) = 0 , T.K. ONI QWLQ- @TSQ KON_@NKTAMI FUNKCII f . oTS@DA SLEDUET, ^TO DIZ_@NKCIQ

Pi(a1; : : : ; an) PO WSEM ZNA^ENIQM i = 1; 2; : : : ; k TOVE RAWNA 0 I ISKOMOE RAWENSTWO WERNO.

2) f(a1; : : : ; an) = 1 , TOGDA KON_@NKT K = x1a1 xa22 : : : xann RAWEN 1 NA \TOM NABORE. eSLI KON_@NKT K QWLQETSQ PROSTYM, TO ON IME-

ETSQ SREDI P1; P2 ; : : : ; Pk I, SLEDOWATELXNO, IH DIZ_@NKCIQ RAWNA 1 NA NABORE (a1 ; : : : ; an) . eSLI K NE QWLQETSQ PROSTYM, TO UDALENIEM NEKOTORYH SOMNOVITELEJ IZ NEGO POLU^AETSQ ODIN IZ PROSTYH KON_- @NKTOW, KOTORYJ I RAWEN 1 NA NABORE (a1; : : : ; an) I, ZNA^IT, SNOWA DIZ_@NKCIQ WSEH PROSTYH KON_@NKTOW RAWNA 1. tEOREMA DOKAZANA.

sLEDSTWIE. mINIMALXNAQ dnf POLU^AETSQ IZ SOKRA]ENNOJ UDALENIEM NEKOTORYH PROSTYH KON_@NKTOW (LIBO RAWNA EJ).

kAKIE IMENNO PROSTYE KON_@NKTY NADO UDALITX IZ SOKRA]ENNOJ dnf DLQ POLU^ENIQ MINIMALXNOJ dnf MOVNO UZNATX IZ TABLICY ISTINNOSTI DLQ PROSTYH KON_@NKTOW, SM. NIVE.

pRIMER 1. nAJTI SOKRA]ENNU@ I MINIMALXNU@ dnf FUNKCII f(x; y; z) = (1100 0111)T = (0; 1; 5; 6; 7) .

11

rE[ENIE. wYPI[EM STRO^KI 0; 1; 5;6; 7 , NA KOTORYH FUNKCIQ ISTINNA, TOGDA EE SOWER[ENNAQ dnf WYGLQDIT TAK:

f(x; y; z) = x0y0z0 _ x0 y0z1 _ x1y0z1 _ x1y1z0 _ x1y1z1 .

nAHOVDENIE WSEH PROSTYH KON_@NKTOW BUDEM PROWODITX UDALQQ PEREMENNYE PO PRAWILU SKLEIWANIQ AB _ AB = A OTTALKIWAQSX OT SOWER[ENNOJ dnf FUNKCII f . wMESTO KON_@NKTA K = x y z BUDEM PISATX SAMU STROKU ( ; ; ) , PO KOTOROJ K OBRAZOWAN. pROCEDURA SKLEIWANIQ BUDET WYGLQDETX TAK: 110 _ 010 = ;10 WMESTO

nABORY 0;1; 5; 6; 7 NA KOTORYH f RAWNA 1 ZAPI[EM, SORTIRUQ IH W GRUPPY PO KOLI^ESTWU EDINIC, I NAHODIM WSE WARIANTY DLQ PRIMENENIQ PRAWILA SKLEIWANIQ (SKLEIWA@]IESQ STRO^KI NAHODQTSQ W SOSEDNIH GRUPPAH). w REZULXTATE, SKLEIWANIEM KON_@NKTOW (0) I (1), (1) I (5), (5) I (7), (6) I (7), POLU^IM ZAMENQ@]IE IH KON_@NKTY

(0; 1) = 00; , (1; 5) = ;01 , (5; 7) = 1 ;1 , (6; 7) = 11; . kON_@NKTY

(0), (1), (5), (6) I (7) W REZULXTATE SKLEIWANIQ PROPALI. w ITOGE, OSTALISX ^ETYRE KON_@NKTA: 00; , ;01 , 1 ; 1 I 11; . pRAWILO SKLEIWANIQ PRIMENITX K NIM NEWOZMOVNO I W REZULXTATE POLU^I-

LASX SOKRA]ENNAQ dnf: f(x; y; z) = (00;)_(;01)_(1;1)_(11;) =

= x y _ yz _ xz _ xy .

pO TABLICE ISTINNOSTI DLQ PROSTYH KON_@NKTOW WIDNO (SM. TABL. 13), ^TO KON_@NKTY x y I xy NELXZQ UDALITX, A IZ DWUH OSTAW- [IHSQ KON_@NKTOW MOVNO ODNOGO UDALITX, T.E. f(x; y; z) IMEET DWE

MINIMALXNYE dnf: f(x; y; z) = x y _ yz _ xy = x y _ xz _ xy .

12

x7. rELEJNO-KONTAKTNYE SHEMY

oPREDELENIE 1. kONTAKTOM (PEREKL@^ATELEM, DWUHPOL@SNIKOM) NAZYWAETSQ USTROJSTWO, KOTOROE MOVET IMETX DWA SOSTOQNIQ: 0 I 1. eSLI K IME@]IMSQ U USTROJSTWA DWUM POL@SAM PODATX NAPRQVENIE, TO W SOSTOQNII 1 WOZNIKAET TOK, A W SOSTOQNII 0 USTROJSTWO TOK NE PROPUSKAET.

fIZI^ESKI KONTAKTY MOVNO REALIZOWATX S POMO]X@ RELE ILI SOOTWETSTWU@]IH TRANZISTORNYH SHEM.

iZ KONTAKTOW, SOEDINQQ IH W POL@SAH, MOVNO SOBRATX KONTAKTNU@ SHEMU, W KOTOROJ WYDELQ@TSQ DWA POL@SA I PODAETSQ NA NIH NAPRQVENIE. w ZAWISIMOSTI OT SOSTOQNIJ KONTAKTOW WSQ SHEMA LIBO PROPUSKAET TOK (SOSTOQNIE 1), LIBO NE PROPUSKAET (SOSTOQNIE 0). eSLI SOSTOQNIQ KONTAKTOW PRINADLEVAT fx1; x1; x2; x2; : : : ; xn; xng , TO SOSTOQNIE SHEMY QWLQETSQ BULEWOJ FUNKCIEJ y = f(x1 ; x2; : : : ; xn) , KOTORAQ NAZYWAETSQ FUNKCIEJ PROWODIMOSTI SHEMY.

sWOJSTWO 1. eSLI SHEMA SOSTOIT IZ KONTAKTOW x1 I x2 , SOEDINENNYH POSLEDOWATELXNO (SM. RIS. 1), TO ONA IMEET FUNKCI@ PROWODIMOSTI y = x1 x2 ; ESLI VE SHEMU SOSTAWITX IZ KONTAKTOW x1 I x2 , SOEDINENNYH MEVDU SOBOJ PARALLELXNO (SM. RIS. 2), TO EE FUNKCIEJ PROWODIMOSTI BUDET y = x1 _ x2 .

tEOREMA O KONTAKTNOJ SHEME. pO L@BOJ BULEWOJ FUNKCII f MOVNO POSTROITX KONTAKTNU@ SHEMU, DLQ KOTOROJ f QWLQETSQ FUNKCIEJ PROWODIMOSTI.

dOKAZATELXSTWO. eSLI f(x1; x2; : : : ; xn) 0 , TO EJ SOOTWETSTWUET SHEMA NE IME@]AQ KONTAKTOW. eSLI VE f(x1; x2; : : : ; xn) 60 , TO EE MOVNO REALIZOWATX W dnf. kAVDU@ \LEMENTARNU@ KON_@NKCI@, IZ KOTORYH SOSTOIT dnf, REALIZUEM POSLEDOWATELXNOJ CEPO^- KOJ KONTAKTOW, MEVDU SOBOJ \TI CEPO^KI SOEDINIM PARALLELXNO. pOLU^ENNAQ SHEMA IMEET f SWOEJ FUNKCIEJ PROWODIMOSTI. tEOREMA DOKAZANA.

pRIMER 1. pOSTROITX KONTAKTNU@ SHEMU, FUNKCIEJ PROWODIMOS-

TI KOTOROJ QWLQETSQ f(x; y; z) = (1100 0111)T = (0;1; 5; 6; 7) .

rE[ENIE. w PREDYDU]EM PARAGRAFE DLQ \TOJ FUNKCII BYLI NAJDENY DWE MINIMALXNYE dnf. wOZXMEM ODNU IZ NIH, NAPRIMER,

13

f(x; y; z) = x y_xz _xy . eSLI PO \TOJ dnf POSTROITX SHEMU, TO ONA BUDET SOSTOQTX IZ 6 KONTAKTOW, ESLI VE \TU dnf PREDWARITELXNO PREOBRAZOWATX TAK: f(x; y; z) = x y _ x(z _ y) , TO MOVNO POSTROITX SHEMU IZ 5 KONTAKTOW, IZOBRAVENNU@ NA RIS. 3.

x8. mINIMIZACIQ dnf S POMO]X@ KART kARNO

kARTA kARNO PREDSTAWLQET IZ SEBQ TABLICU ISTINNOSTI BULEWOJ FUNKCII, ZAPISANNU@ SPECIALXNYM KOMPAKTNYM SPOSOBOM I POZWOLQ@]U@ BYSTRO NAHODITX MINIMALXNU@ dnf, OSOBENNO DLQ FUNKCIJ TREH I ^ETYREH ARGUMENTOW.

kARTA kARNO DLQ FUNKCII f(x; y) = (a; b; c; d)T IMEET WID, PRIWEDENNYJ W TABL. 9. nOMERA STRO^EK STANDARTNOJ TABLICY ISTINNOSTI MY ZAPISALI W SOOTWETSTWU@]IH KLETKAH KARTY kARNO.

oTRAVAQ \TU KARTU SIMMETRI^NO OTNOSITELXNO OTNOSITELXNO PRAWOJ ILI NIVNEJ GRANICY POLU^AEM KARTU kARNO DLQ TREH PEREMENNYH, SM. TABL. 10. mOVNO PRODOLVITX PROCESS OTRAVENIQ I DALX[E, POLU^AQ KARTY kARNO DLQ ^ETYREH, PQTI I BOLX[EGO ^ISLA PEREMENNYH. kARTY kARNO DLQ ^ETYREH I PQTI PEREMENNYH PRIWEDENY NIVE, SM. TABL. 11 I 12.

pO KARTE kARNO MOVNO LEGKO NAHODITX SKLEIWA@]IESQ KON_- @NKTY DANNOJ FUNKCII. tAKIM KON_@NKTAM SOOTWETSTWU@T KLETKI NA KARTE kARNO, QWLQ@]IESQ SIMMETRI^NYMI DRUG DRUGU OTNOSITELXNO TEH WERTIKALXNYH ILI GORIZONTALXNYH LINIJ, OTNOSITELXNO KOTORYH PROISHODIL PROCESS OTRAVENIQ PRI POSTROENII KARTY kARNO. nAPRIMER, W TABL. 12 KLETKI 19 I 23 SKLEIWA@TSQ, A 19 I 20 NE SKLEIWA@TSQ.

pRIMER 1. nAJTI SOKRA]ENNU@ I MINIMALXNU@ dnf FUNKCII f(x; y; z) = (1111 0010)T , POSTROITX KONTAKTNU@ SHEMU PO MINIMALXNOJ dnf.

14

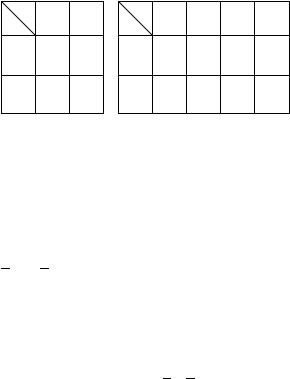
rE[ENIE. iZOBRAZIM ISTINNOSTNU@ TABLICU DLQ f W WIDE KARTY kARNO (SM. TABL. 10).

nA KARTE kARNO SKLEIWA@]IESQ KON_@NKTY | \TO SIMMETRI^- NYE KLETKI, PRI \TOM KLETKI (0) I (4) S^ITA@TSQ SIMMETRI^NYMI S KLETKAMI (2) I (6), SOOTWETSTWENNO. nA 1 \TAPE SKLEIWAQ KLETKI (0)

I (1), (0) I (2), (1) I (3), (2) I (3), (2) I (4), POLU^AEM INTERWALY RAN-

GA 1; NA 2 \TAPE, SKLEIWAQ SIMMETRI^NYE INTERWALY RANGA 1 (0; 1) c (2;3) ILI (0; 2) S (1; 3) , POLU^AEM INTERWAL (0; 1; 2; 3) RANGA 2. w ITOGE MNOVESTWO EDINIC FUNKCII f POKRYTO MAKSIMALXNYMI INTERWALAMI (0; 1; 2; 3) I (2; 6) , KOTORYE I DA@T PROSTYE KON_@NKTY:

x I yz .

pOLU^ENNAQ SOKRA]ENNAQ dnf, W \TOM PRIMERE, QWLQETSQ I MINIMALXNOJ, T.K. PRI UDALENII L@BOGO IZ \TIH INTERWALOW MY NE POKRYWAEM MNOVESTWA WSEH EDINIC. w \TOM MOVNO UBEDITXSQ I S POMO]X@ TABLICY ISTINNOSTI DLQ PROSTYH KON_@NKTOW.

kONTAKTNAQ SHEMA S FUNKCIEJ PROWODIMOSTI f(x; y; z) STROITSQ PO MINIMALXNOJ dnf yz _ x (SM. RIS. 4).

pRIMER 2. nAJTI MINIMALXNU@ dnf I POSTROITX KONTAKTNU@ SHEMU DLQ FUNKCII f(a; b; c; d) = (2; 4 ; 6; 8 ; 14) .

rE[ENIE. iZOBRAZIM ISTINNOSTNU@ TABLICU DLQ f W WIDE KARTY kARNO (SM. TABL. 11). oNA IMEET 11 INTERWALOW RANGA 0 | \TO KLETKI, GDE f RAWNA 1. sKLEIWAQ SIMMETRI^NYE INTERWALY RANGA 0 POLU^AEM 16 INTERWALOW RANGA 1: (2; 6) ; (6; 14) ; (14; 10) ; (2; 10) I T.D. pRI \TOM, KLETKI (0), (1), (3), (2) QWLQ@TSQ SIMMET-

RI^NYMI S (8), (9), (11), (10), A KLETKI (0), (4), (12), (8) SIMMET-

RI^NY (2), (6), (14), (10) SOOTWETSTWENNO. sKLEIWAQ SIMMETRI^NYE INTERWALY RANGA 1 POLU^AEM 6 INTERWALOW RANGA 2: (2; 6;14; 10) ;

15

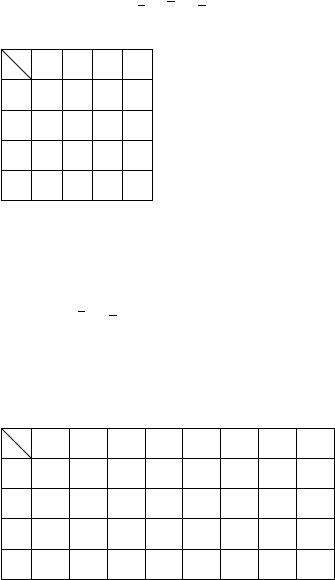
(8; 9; 11; 10) ; (12; 8; 14; 10) ; (4; 12; 6; 14) ; (12; 13; 8;9) ; (4; 5;12; 13) .

|TI 6 INTERWALOW QWLQ@TSQ MAKSIMALXNYMI, T.K. DALXNEJ[EE IH SKLEIWANIE NEWOZMOVNO I W REZULXTATE POLU^AETSQ SOKRA]ENNAQ

dnf: f(a; b; c; d) = ab _ bc _ cd _ ac _ bd _ ad .

tABLICA 11

pRI POSTROENII MINIMALXNOJ dnf MY ZAME^AEM, ^TO INTERWA-

LY (2; 6; 14; 10) , (8; 9; 11; 10) , (4; 5; 12;13) UDALITX NELXZQ, INA^E NE BUDUT POKRYTY KLETKI (2), (11) I (5), SOOTWETSTWENNO. pOSKOLXKU \TI OSTAW[IESQ INTERWALY UVE DA@T POKRYTIE WSEGO MNOVESTWA EDINIC FUNKCII f , TO OSTALXNYE KON_@NKTY MOVNO UDALITX. tAKIM OBRAZOM, ab _ bc _ cd | MINIMALXNAQ dnf, SHEMA KOTOROJ IZOBRAVENA NA RIS. 5.

w ZAKL@^ENIE, PRIWEDEM KARTU kARNO DLQ FUNKCII PQTI PERE-

MENNYH f(a; b; c; d; e) = (3; 4; 6; 7; 12; 14; 19; 20; 21; 23; 28;29) .

x9. mINIMIZACIQ dnf METODOM PREOBRAZOWANIJ

dLQ POLU^ENIQ SOKRA]ENNOJ dnf PRIMENQ@T K DANNOJ dnf DWA PRAWILA:

1) xA _ xB = xA _ xB _ AB

2) A _ AB = A { POGLO]ENIE.

tEOREMA O POLU^ENII SOKRA]ENNOJ dnf PO PRAWILAM OBRAZOWANIQ SO@ZOW I POGLO]ENIQ. eSLI K dnf FUNKCII f

PRIMENQTX PRAWILO POGLO]ENIQ I PRAWILO OBRAZOWANIQ SO@ZA, NE POGLO]AEMOGO DRUGIMI KON_@NKTAMI, TO NASTUPIT MOMENT, KOGDA NI ODNO IZ \TIH PRAWIL NE BUDET PRIMENIMO I W \TOT MOMENT POLU- ^ITSQ SOKRA]ENNAQ dnf FUNKCII f(x1; : : : ; xn) .

dOKAZATELXSTWO TEOREMY BUDET SOSTOQTX IZ TREH ^ASTEJ.

1. pOSKOLXKU IZ PEREMENNYH MOVNO OBRAZOWATX LI[X KONE^NOE ^ISLO RAZLI^NYH \LEMENTARNYH KON_@NKCIJ, TO W SLU^AE BESKONE^NOJ WOZMOVNOSTI PRIMENENIQ PRAWIL 1) I 2) NEKOTORYJ KON_@NKT K BUDET POGLO]ATXSQ, A ZATEM POQWLQTXSQ WNOWX W KA^ESTWE SO@ZA. pUSTX K POGLO]AETSQ KON_@NKTOM K1 , K1 POGLO]AETSQ K2 I T.D., Kl;1 POGLO]AETSQ Kl . nO OTS@DA SLEDUET, ^TO K POGLO]AETSQ Kl I PO\TOMU ON NE MOVET POQWITXSQ WNOWX, T.K. BUDET SRAZU POGLO]EN KON_@NKTOM Kl . tAKIM OBRAZOM, PROCESS PRIMENENIQ PRAWIL POGLO]ENIQ I OBRAZOWANIQ NEPOGLO]AEMYH SO@ZOW PREKRATITSQ I MY POLU^IM W REZULXTATE NEKOTORU@ dnf P1 _ P2 _ : : : Pm , SOSTOQ]U@ IZ KON_@NKTOW Pi DANNOJ FUNKCII f .

2. uBEDIMSQ, ^TO W dnf P1 _ P2 _ : : : Pm SODERVATSQ WSE PROSTYE KON_@NKTY FUNKCII f . eSLI KAKOGO-TO PROSTOGO KON_@NKTA P NET SREDI Pk , TO, WWIDU SWOEJ PROSTOTY, P OBLADAET SWOJSTWOM, ^TO NI ODIN IZ KON_@NKTOW Pk NE MOVET WHODITX W P W KA^ESTWE

WREMQ, NI ODIN IZ Pk NE BUDET SOMNOVITELEM S . |TO OZNA^AET, ^TO

SNEPOGLO]AEMYJ SO@Z Pi I Pj , A \TO PROTIWORE^IT USLOWI@.

3.iTAK, W dnf P1 _ P2 _ : : : Pm SODERVATSQ WSE PROSTYE KON_- @NKTY. lEGKO PONQTX, ^TO NEPROSTYH KON_@NKTOW W NEM NET, INA^E MOVNO BYLO BY PRIMENITX PRAWILO POGLO]ENIQ.

tEOREMA POLNOSTX@ DOKAZANA.

dLQ POLU^ENIQ MINIMALXNOJ dnf IZ SOKRA]ENNOJ MOVNO ISPOLXZOWATX TABLICU ISTINNOSTI DLQ PROSTYH KON_@NKTOW.

pRIMER 1. nAJTI SOKRA]ENNU@ I MINIMALXNU@ dnf, POSTROITX KONTAKTNU@ SHEMU DLQ f(a; b; c) = (a b)(b ! (a c)) _ a ! c .

rE[ENIE. iSKL@^AQ OPERACII !; ; POLU^AEM, ^TO

f(a; b; c) = (ab _ ab)(b _ ac _ ac) _ a _ c .

dALEE PRIMENQEM ZAKONY DE mORGANA, RASKRYWAEM SKOBKI I POSLE UPRO]ENIJ POLU^AEM DIZ_@NKTIWNU@ FORMU:

OSTAW[IHSQ KON_@NKTOW MOVNO ODNOGO UDALITX, TAKIM OBRAZOM

f(a; b; c) = ab _ ac _ ab = ab _ bc _ ab { DWE MINIMALXNYE dnf.

dLQ POSTROENIQ KONTAKTNOJ SHEMY, MOVNO IH PREOBRAZOWATX TAK:

ab _ a(b _ c) , b(a _ c) _ ab .

18

x10. kON_@NKTIWNAQ NORMALXNAQ FORMA (knf)

tEOREMA O REALIZACII BULEWOJ FUNKCII W SOWER[ENNOJ knf. dLQ L@BOJ FUNKCII f(x1; x2; : : : ; xn) , NE RAWNOJ TOVDEST-

KOTORYH FUNKCIQ f RAWNA 0.

mINIMIZACI@ knf PROWODQT ANALOGI^NO MINIMIZACII dnf. eSLI FUNKCIQ ZADANA TABLI^NO, TO DLQ MINIMIZACII knf PRIMENQ@T PRAWILO SKLEIWANIQ (x _ y)(x _ y) = x K SOWER[ENNOJ knf, MOVNO ISPOLXZOWATX I KARTY kARNO. eSLI FUNKCIQ ZADANA S POMO]X@ PROPOZICIONALXNOJ FORMULY, TO WNA^ALE POLU^A@T L@BU@ knf, ZATEM PRIMENQ@T K NEJ PRAWILO POGLO]ENIQ (x _ y)x = x I PRAWILO REZOL@CIJ (x _ y)(x _ z) = (x _ y)(x _ z)(y _ z) DO TEH POR POKA MOVNO PRIMENQQ IH POLU^ATX NEPOGLO]AEMYE REZOLXWENTY.

oPREDELENIE 1. fORMULA F WYWODIMA IZ FORMUL F1 ; F2; : : : ; Fn ,

OBOZNA^AETSQ F1; F2; : : : ; Fn ` F , ESLI F1 F2 : : : Fn ! F 1 .

F1F2 : : : Fn ! F = F1F2 : : : FnF . sLEDSTWIE. F1F2 : : : Fn ` F , F1F2 : : : FnF 0 .

dLQ PROWERKI LOVNOSTI F1F2 : : : FnF MOVNO PRIWESTI \TU FORMULU K knf I S POMO]X@ PRAWILA REZOL@CIJ POLU^ITX PROIZWEDENIE WIDA pp , QWLQ@]EESQ TOVDESTWENNO LOVNYM.

pRIMER 1. dOKAZATX, ^TO F1; F2; F3; F4; F5 ` F6 , GDE F1 = p_r_t ,

F2 = r , F3 = t _ p _ r , F4 = t _ q , F5 = p _ q _ r , F6 = q .

rE[ENIE. rASSMOTRIM KON_@NKCI@ F1F2 F3F4F5F6 ^TO ONA TOVDESTWENNO LOVNA, DOBAWLQQ REZOLXWENTY:

F7 = p _ t { REZOLXWENTA F1; F2 ; F8 = t { REZOLXWENTA F4; F6 ; F9 = p { REZOLXWENTA F7; F8 ;

F10 = p _ q

F11 = p { REZOLXWENTA F10 ;F 6 .

w REZULXTATE POLU^ILI KON_@NKCI@ F9 F11 = pp 0 , ^TO I TREBOWALOSX DOKAZATX.

zAME^ANIE. w PRIWEDENNOJ PRIMERE WSE \LEMENTARNYE DIZ_@NKCII SODERVALI NE BOLEE ODNOJ POZITIWNOJ PEREMENNOJ, TAKIE DIZ_-

19

@NKCII NAZYWA@TSQ DIZ_@NKTAMI hORNA. w \TOM SLU^AE UDOBNO POLU^ATX REZOLXWENTY ODINO^NYH POZITIWNYH PEREMENNYH I DIZ_- @NKTOW, IME@]IH OTRICANIE TOJ VE PEREMENNOJ.

x11. fUNKCIONALXNYE SHEMY

oPREDELENIE 1. fUNKCIONALXNYM \LEMENTOM NAZYWAETSQ USTROJSTWO, IME@]EE n UPORQDO^ENNYH WHODOW I ODIN WYHOD; ESLI NA KAVDYJ IZ WHODOW PODATX ODIN IZ SIGNALOW 0 ILI 1, TO ^EREZ WREMQ NA WYHODE BUDET REZULXTAT: 0 ILI 1.

w DALXNEJ[EM BUDEM RASSMATRIWATX TOLXKO SLU^AJ = 0 , TAKIE \LEMENTY NAZYWA@TSQ 0-TAKTNYMI.

iZ OPREDELENIQ SLEDUET, ^TO KAVDYJ FUNKCIONALXNYJ \LEMENT REALIZUET NEKOTORU@ BULEWU FUNKCI@ y = f(x1; x2; : : : ; xn) , IZOBRAVENIE SM. NA RIS. 6.

oPREDELENIE 2. pONQTIE FUNKCIONALXNOJ SHEMY DAETSQ INDUKTIWNO:

1)L@BOJ FUNKCIONALXNYJ \LEMENT S^ITAETSQ FUNKCIONALXNOJ SHEMOJ, WHODAMI I WYHODOM SHEMY QWLQ@TSQ WHODY I WYHOD \TOGO \LEMENTA;

2)ESLI S0 I S1 | FUNKCIONALXNYE SHEMY, TO MOVNO POLU^ITX NOWU@ SHEMU S , SOEDINIW WYHOD S1 S ODNIM IZ WHODOW S0 ; PRI \TOM

WYHODOM S QWLQETSQ WYHOD S0 , A WHODAMI S BUDUT WSE WHODY S0 I S1 , KROME TOGO WHODA S0 , S KOTORYM SOEDINEN WYHOD S1 (SM. RIS. 7); 3) ESLI S | FUNKCIONALXNAQ SHEMA, TO MOVNO POLU^ITX NOWU@ SHEMU S0 , OTOVDESTWIW (SOEDINIW) NESKOLXKO WHODOW S ; PRI \TOM WYHOD S0 SOWPADAET S WYHODOM S , A WHODAMI S0 QWLQ@TSQ WHODY S , PRI \TOM SOEDINENNYE WHODY S^ITA@TSQ ZA ODIN WHOD (SM. RIS. 8).

20