Лекции / ИК-спектроскопия

ИК- спектроскопия

Раздел.1. Теоретические основы метода.

1. Введение. ИК-спектроскопия - спектральный метод анализа, в основе которого лежит взаимодействие инфракрасного излучения с веществом.

Свет поглощается веществом избирательно: при некоторых длинах волн светопоглощение происходит интенсивно, а при некоторых - свет (электромагнитное излучение) не поглощается. Интенсивно поглощаются кванты света, энергия которых hν равна энергии возбуждения частицы, вероятность поглощения таких квантов больше 0. Молярный коэффициент поглощения ɛ при этих частотах (ν) достигает больших значений.

Распределение по частотам (или по длинам волн) значений молярного коэффициента (оптических плотностей, интенсивности света, прошедшего через поглощающую среду) называется спектром поглощения. Наибольший интерес представляют следующие характеристики спектра: число максимумов (или полос поглощения), их положение по шкале длин волн, высота максимумов, форма полос поглощения.

Появление полос поглощения обусловлено дискретностью энергетических состояний поглощающих частиц и квантовой природой электромагнитного излучения. Интенсивно поглощаются кванты света, которые соответствуют энергии возбуждения частицы. При поглощении квантов света происходит увеличение внутренней энергии частицы, которая складывается из энергии вращения частицы как целого, энергии колебания атомов в молекуле и энергии движения электронов: Е = Е_вр. + Е_кол. + Е_эл.

Сюда же надо суммировать энергии тонкой и сверхтонкой структуры, связанные с электронным и ядерным спином, и другие слагаемые, которыми в первом приближении можно пренебречь.

По энергии вращательное, колебательное и электронное движение различаются следующим образом: Е_вр. << Е_кол. << Е_эл. Для возбуждения вращения молекулы требуется энергия, примерно в тысячу раз меньшая, чем энергия для возбуждения колебаний. Для возбуждения высших энергетических состояний валентных электронов требуется энергия, примерно в тысячу раз большая, чем энергия для возбуждения колебаний атомов.

2. Вращательные спектры

Вращательную энергию молекул и, соответственно, вращательные переходы в молекуле рассматривают с помощью модели жесткого ротора (волчка), который представляет собой две массы, которые находятся друг от друга на фиксированном расстоянии (для двухатомной молекулы) (Рис.1).

r₁ r₂

.

.. m₁ m₂

s

r₀

Рис.1 – Модель жесткого ротора, где s – центр масс двухатомной молекулы, m₁ и m₂ – массы атомов, r₁ и r₂ – расстояния от центров соответствующих атомов до s, r₀ – фиксированное расстояние между атомами.

Вращательные переходы, как и другие изменения внутренней энергии микрочастиц, квантуются. Возможные значения энергии вращательных состояний зависят от момента инерции и вращательного квантового числа:

Е_вр =( h²/8π²I)∙J(J+1), (1)

где I – момент инерции молекулы (I = (m₁ m₂/ m₁+ m_)∙ r₀²), J = 0, 1, 2, 3, 4… - вращательное квантовое число.

Возбуждение вращательных уровней энергии происходит уже при поглощении далекого ИК и микроволнового излучения с длинами волн λ ≥ 10² мкм, которым соответствует энергия ≤ 1,2 кДж/моль.

Чисто вращательные спектры в аналитических целях не используются сейчас.

3. Колебательные спектры

В ИК-спектроскопии обычно спектры представляют собой распределение интенсивности света по волновым числам. Волновое число ν =1/λ, величина, обратная длине волны, измеряется в обратных сантиметрах см^-1.

Полосы, связанные с возбуждением колебательных уровней энергии, расположены в области спектра от 200-300 до 4000-5000 см^-1, что соответствует энергии квантов от 3 до 60 кДж/моль. Отсюда следует, что при обычных температурах энергетическое состояние молекул (как правило) характеризуется основным колебательным уровнем с квантовым колебательным числом V₀.

Простейшей моделью, которая используется при рассмотрении колебаний двухатомной молекулы, является модель гармонического осциллятора. Это система из двух масс, связанных упруго. При возбуждении колебаний такой молекулы межатомное расстояние увеличивается на величину ∆r. При этом возникает сила упругости: F = -k∆r, где k – силовая постоянная (в первом приближении характеризует прочность связи в молекуле). Согласно второму закону Ньютона:

F = M (d²(∆r)/dr²), (2)

где М – приведенная масса (1/М = 1/М₁ + 1/М₂).

Решая это дифференциальное уравнение относительно ∆r получаем:

∆r =a∙cos2πν_колt (a=const) (3)

Решая уравнение относительно ν_кол:

ν_кол =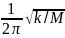 или ṽ = 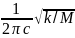в см^-1 (4)

Кривая потенциальной энергии гармонического осциллятора описывается параболой с вершиной, соответствующей равновесному расстоянию между атомами r₀ (Рис.2).

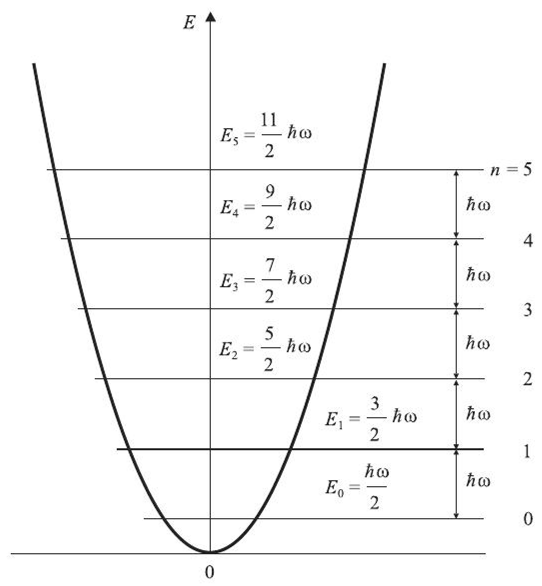
Рис.2.- Кривая потенциальной энергии гармонического осциллятора.

По оси ординат – потенциальная энергия, по оси абсцисс - r, n= 0,1,2,3….. – колебательные квантовые числа, которые в ИК-спектроскопии принято обозначать буквой V = 0, 1, 2, 3, 4, 5…

Частота колебаний для гармонического осциллятора не зависит от ∆r (ур-ие 4). Как и вращательная, колебательная энергия квантуется. Применяя квантовую теорию можно найти, что энергия колебательных переходов следующая:

Е_кол = (V + ½)hν₀, (5)

где V (0, 1, 2, 3, 4) – колебательное квантовое число, ν₀ – частота колебаний, соответствующая основному колебательному уровню с квантовым числом V₀. Из уравнения 5 следует, что колебания происходят всегда, даже при V = 0. Таким колебаниям соответствует энергия

Е_кол = ½hν₀ (6)

Правилами отбора в таких системах разрешены переходы, для которых ∆V = ±1 (7).

Из уравнений 6 и 7 следует, что расстояние между двумя соседними энергетическими уровнями гармонического осциллятора постоянно и равно hν₀. Т.о., в спектре будет наблюдаться только одна полоса с частотой ν_кол = .

В действительности же реальные колебания молекул ангармоничны, а в спектре наблюдается несколько спектральных полос (линий). Причина в том, что поведение молекулы описывается моделью гармонического осциллятора лишь приближенно.

С одной стороны, в ходе колебаний атомы не могут сближаться беспредельно, т.к. с уменьшением межатомного расстояния резко возрастают силы отталкивания. С другой стороны, ∆r не может беспредельно увеличиваться, это приведет к распаду молекулы.

В действительности любая молекула – это ангармонический осциллятор. На рис.3 представлена кривая потенциальной энергии ангармонического осциллятора.

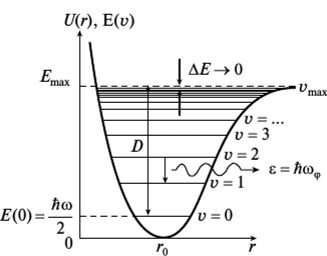
Рис.3 – Кривая потенциальной энергии ангармонического осциллятора.

Энергетические уровни ангармонического осциллятора с увеличением квантового числа сближаются. Их положения ограничены энергией диссоциации молекулы. Разрешены переходы между любыми уровнями, следовательно, в спектре наблюдается несколько полос. Наиболее интенсивной является первая полоса, возникающая при переходе с уровня V=0 на уровень V =1. Этой полосе соответствует основная или фундаментальная частота. Менее интенсивные полосы дают обертоны, т.е. частоты, характеризующие переход с уровня V=0 на уровень V =2 (первый обертон или вторая гармоника), на уровень V =3 (второй обертон или третья гармоника).

Колебательными или ИК-спектрами обладают не все молекулы, а только те, у которых при колебании происходит изменение их электронного дипольного момента, т.е. полярные молекулы (Напимер, HCl, HBr). Неполярные молекулы (О₂, Н₂ и др.) не обладают ИК-спектрами.

Сравнительная простота колебательных спектров двухатомных молекул обусловлена тем, что колебания происходят только вдоль линии, соединяющей ядра. В многоатомной молекуле колеблются все атомы. Число колебательных степеней свободы у нелинейной молекулы, состоящей из N атомов равно: f = 3N – 6, а у линейной f = 3N – 5.

Принять называть колебания в многоатомной молекуле нормальными колебаниями. Частота нормальных колебаний характеризуется положением пол

Число нормальных колебаний равно числу колебательных степеней свободы.

Нормальные колебания подразделяются на:

• валентные и

• невалентные (деформационные).

Валентные колебания - это колебания, в результате которых происходит изменение длины связи без существенного изменения углов между связями. Обозначают их v.

Невалентные (деформационные) происходят с изменением угла связи, обозначают их δ.

Пример. Нормальные колебания молекулы воды H₂O.

f = 3∙3 – 6 = 3 – число нормальных степеней свободы. У молекулы воды 2 типа валентных колебаний и один тип деформационных.

Валентные колебания

1. v ₁

2. v ₂

3. Невалентные (деформационные) колебания δ

Рис.4. Нормальные колебания молекулы воды.

Рис. 5. Аппаратура для колебательной спектроскопии