
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ ЭЛЕМЕНТОВ ВЫСШЕЙ МАТЕМАТИКИ
.docxТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ ЭЛЕМЕНТОВ ВЫСШЕЙ МАТЕМАТИКИ
КОМПЛЕКСНЫЕ ЧИСЛА
Z=a+bi – алгебраическая форма комплексного числа
«а» и «b» - действительные числа; i2= -1 - мнимая единица
ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ
Чтобы сложить (вычесть) комплексные числа нужно сложить (вычесть) их действительные и мнимые части.
Z1= a1+b1i; Z2=a2+b2i
Z1+Z2= (a1+a2) +(b1+b2) i
Z1-Z2= (a1-a2) +(b1-b2) i
Умножение комплексных чисел производится по правилу умножения многочленов.
Чтобы разделить два комплексных числа, нужно числитель и знаменатель дроби умножить на число, сопряженное знаменателем:
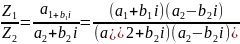
ВОЗВЕДЕНИЕ В СТЕПЕНЬ
i2=-1
i3= i2*i=-i
i4=(i2)2=(-1)2=1
i5=i2*i2*i=1
i6=(i2)3=(-1)3=-1
i7=(i2)3*i= -i
i8=(i2)4=1
ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА
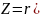
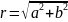 – модуль
комплексного числа
– модуль
комплексного числа
φ- аргумент комплексного числа
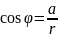 ;
;
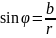
ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ В ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЕ
Z1= r1 (cos φ1+i sin φ2) ; Z2= r2 (cos φ2+i sin φ2)
Z1*Z2= r1*r2 (cos (φ1+φ2)+i sin (φ1+φ2))
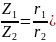
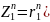
ПОКАЗАТЕЛЬНАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА
Z=r*eiφ
ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ В ПОКАЗАТЕЛЬНОЙ ФОРМЕ
Z1=r1eiφ1 Z2=r2eiφ2
Z1*Z2=r1*r2 ei(φ1+φ2)
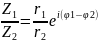
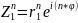
МАТРИЦЫ, ВИДЫ МАТРИЦ, ЭЛЕМЕНТЫ МАТРИЦЫ.
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ МЕТОДОМ КРАМЕРА И ГАУССА.
Прямоугольной
матрицей , порядка m*n
называется таблица составленная из
m;n-
чисел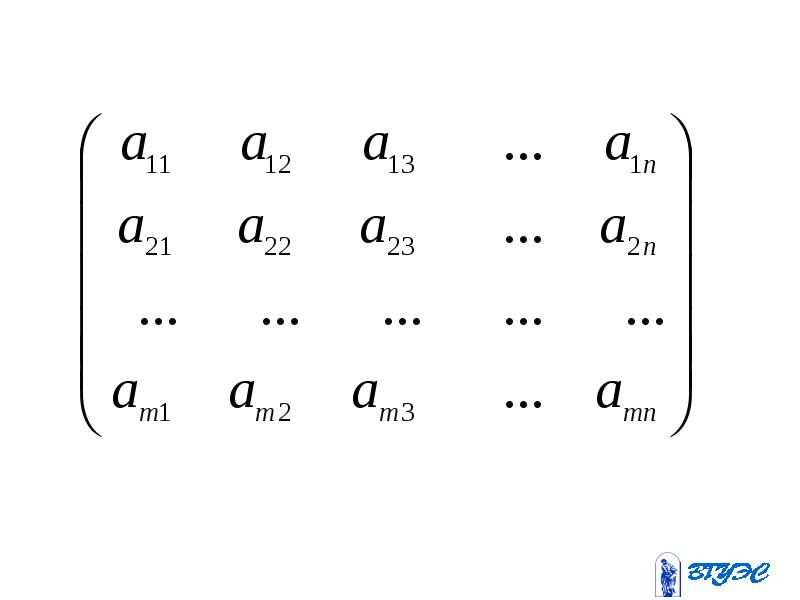
m-число строк
n-число столбцов
aij-элементы
i-номер строки
j-номер столбца
Если число строк равно числу столбцов, матрица называется квадратной.
Элементы: а11, а22, а33 вместе образуют главную диагональ матрицы.
Порядок матрицы определяется числом столбцов n
А=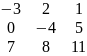 – квадратная матрица 3-го порядка
– квадратная матрица 3-го порядка
-3,-4,11- главная диагональ
7,-4,1- побочная
Е=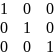 – единичная
– единичная
А=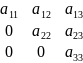 – ступенчатая
– ступенчатая
ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ МАТРИЦ
Строки матрицы можно менять местами
Строку матрицы можно умножить (разделить) на одно и то же отличное от 0 число.
Если в результате преобразований получили пропорциональные строки ( как частный случай равные нулю) , то их можно удалить оставив одну.
К строке матрицы можно прибавить другую строку , умноженную на отличное от 0 число.
Элементарные преобразования используют при решении систем уравнений методом Гаусса
ОПРЕДЕЛИТЕЛИ ВТОРОГО И ТРЕТЬЕГО ПОРЯДКОВ.
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ МЕТОДОМ КРАМЕРА.




МАТЕМАТИЧЕСКАЯ СТАТИСТИКА.
Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных её значений на вероятности этих значений:
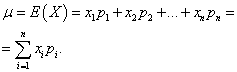
Дисперсией дискретной случайной величины X называется математическое ожидание квадрата отклонения её от математического ожидания:
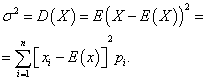
Средним
квадратическим отклонением![]() случайной
величины X называется
арифметическое значение квадратного
корня её дисперсии:
случайной
величины X называется
арифметическое значение квадратного
корня её дисперсии:
![]() .
.
РАСПРЕДЕЛЕНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

ПРИМЕР ГРАФИКА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ДИСКРЕТНОЙ ВЕЛИЧИНЫ
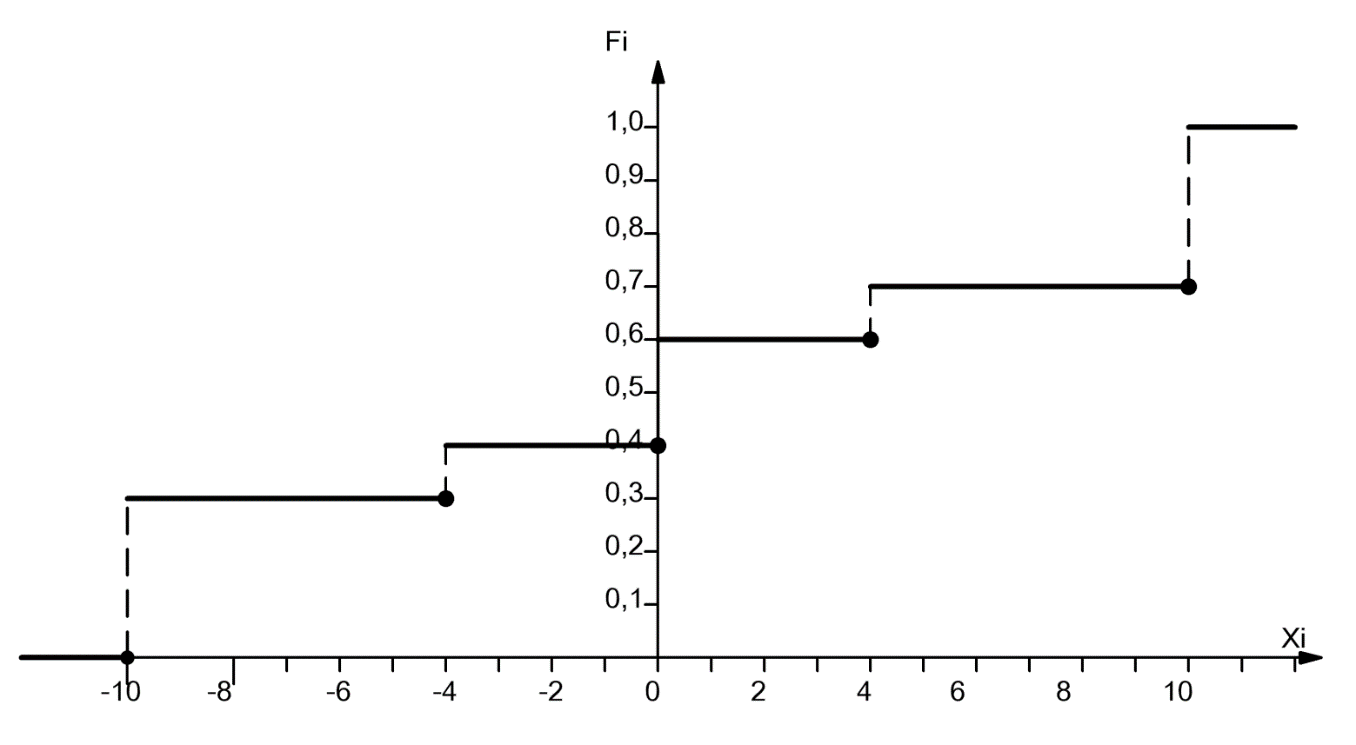
КОМБИНАТОРИКА.
ПЕРЕСТАНОВКИ.СОЧЕТАНИЯ.РАЗМЕЩЕНИЯ.
Факториал (произведение всех натуральных чисел от 1 до n включительно)
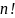
1!=1
2!=1*2=2
3!=1*2*3=6
4!=1*2*3*4=24
5!=1*2*3*4*5=120
6!=1*2*3*4*5*6=720
7!=1*2*3*4*5*6*7=5040
Перестановки. Сочетания, Размещения.
ПЕРЕСТАНОВКИ.
Формула: Pn=n!
Типичная смысловая нагрузка: «Сколькими способами можно переставить n объектов?»
СОЧЕТАНИЯ.
Формула
количества сочетаний:
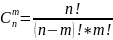
Типичная смысловая нагрузка: «Сколькими способами можно выбрать m объектов из n ?». Поскольку выборка проводится из множества, состоящего из n объектов, то справедливо неравенство 0 m n
РАЗМЕЩЕНИЯ.
Формула
количества размещений:

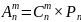
Типичная смысловая нагрузка: «сколькими способами можно выбрать m объектов (из n объектов) и в каждой выборке переставить их местами (либо распределить между ними какие-нибудь уникальные атрибуты)»
КОМБИНАТОРНОЕ ПРАВИЛО СУММЫ И КОМБИНАТОРНОЕ ПРАВИЛО ПРОИЗВЕДЕНИЯ.
Если объект A можно выбрать из некоторого множества объектов m способами, а другой объект B – n способами, то выбор объекта A или объекта B (без разницы какого) возможен m n способами.
Если объект A можно выбрать из некоторого множества объектов m способами и после каждого такого выбора объект B можно выбрать n способами, то упорядоченная пара объектов (A; B) может быть выбрана mn способами.
Данные принципы справедливы и для бОльшего количества объектов. Важная содержательная часть правил состоит в том, знак «плюс» понимается и читается как союз ИЛИ, а знак «умножить» – как союз И.
