10.Линейный двоичный блочный код. Кодирование и декодирование. Синдром. Аппаратные средства создания и проверки данного кода.

Линейный двоичный блочный код состоит из информационной части и проверочной. Проверочные или добавочные символы определяются с помощью поражающей матрицы путем умножения символа информационно части на символ, порождающий матрицы, с последующим сложением по модулю два. С помощью проверочных символов осуществляется обнаружение и исправление ошибок

С индромом называется вектор, который определяет разряд, в котором принятая кодовая комбинация содержит ошибку. Для нахождения требуется вычисления контрольных символов. Они определяется тем же методом, что и проверочные.

Средства кодирования и декодирования линейным двоичным блочным кодом:

Кодирование осуществляется помощью регистра сдвига и сумматоров по модулю 2. Регистр обязательно содержит в себе столько триггеров, сколько разрядов в нашей кодовой комбинации. Информация в триггеры записывается параллельно, а выдается последовательно. Сначала (до кодирования) в четыре первых триггера записывается информационная часть будущей кодовой комбинации. Далее, выходы этих триггеров соединяются со входами сумматоров по модулю 2. Соединения проводятся в соответствии со столбцами матрицы коэффициентов.

Для декодирования используется тот же регистр сдвига и те же сумматоры по модулю 2.

11. Непрерывные помехоустойчивые коды. Сверточный код. Кодирование (схема кодера) и декодирование (решетчатая диаграмма – иметь схему с собой на листочке).

Коды, в которых операции кодирования и декодирования производятся непрерывно над последовательностью посылок без деления их на блоки, называются непрерывными.

Сверточный код относится к подклассу не блочных помехоустойчивых кодов, когда исходная непрерывная последовательность двоичных символов b, проходя через кодер, преобразуется в выходную последовательность c, причем выходных символов больше, чем входных.

Рассмотрим пример кодирования:

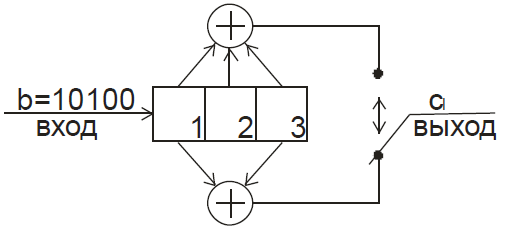Кодер строится на основе регистра сдвига, и сумматоров по модулю 2. Общее соотношение, по которому строится кодер для сверточного кодирования: ν>n>k, где ν – число триггеров в регистре (длина регистра); n – число сумматоров; k – количество символов последовательности b, подающихся на вход кодера за один такт его работы.

Порядок следования слева-направо:

Т1] верхний сумматор: 1⊕0⊕0=1; нижний сумматор 1⊕0=1; Т2] верхний сумматор: 0⊕1⊕0=1; нижний сумматор 0⊕0=0

Т3] верхний сумматор: 1⊕0⊕1=0; нижний сумматор 1⊕1=0; Т4] верхний сумматор: 0⊕1⊕0=1; нижний сумматор 0⊕0=0

Т5] верхний сумматор: 1⊕0⊕0=1; нижний сумматор 1⊕0=1;

Декодирование сверточного кода осуществляется с помощью решетчатой диаграммы. Эта диаграмма устанавливает связи между всеми возможными комбинациями битов, которые могут быть поданы на вход кодера, и выходных битов кодера, а также состояний кодера.

12. Алгоритм оптимального приема цифрового сигнала в шумах по порогу принятия решения. Критерии выставления порога: максимальное правдоподобие и максимум апостериорной вероятности (вывод значений порогов).

Приемник всегда работает по порогу принятия решения. Рассмотрим порог U0. Этот порог делит ось z на две части. Теперь, если амплитуда входного сигнала окажется левее порога (Z<U0), то принимается решение, что был передан S0*, а если Z≥U0, это значит, что был передан S1 *. «Звездочка» здесь означает решение приемника, т.е. оценка входного сигнала

Критерий максимального правдоподобия. Для этого критерия важно знать только плотности распределения вероятностей. Порог U0, выставляется в точке, где плотности равны между собой.

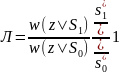
Критерий максимум апостериорной вероятности. Для этого критерия важно знать не только плотности распределения вероятностей, но и априорные вероятности.

Вывод формулы: Апостериорная вероятность посылки сигнала S1 в канал равна , а сигнала S0

Тогда приемник будет принимать то решение, для которого апостериорная вероятность окажется больше: (1)

Мы имеем два последовательных события – а) был передан в канал связи сигнал, например, S1 и б) он был оценен приемником как Zk. Совместная вероятность этих событий:

Отсюда:

Подставим в (1): и перенесем

13. Алгоритм оптимального приема цифрового сигнала в шумах по порогу принятия решения. Критерий выставления порога: минимум среднего риска (вывод значения порога).

Критерий минимума среднего риска. Для этого критерия вводится понятие платы за принятие неверного решения. Любое неверное решение наносит ущерб, и ущерб может быть неодинаков от ошибок разного вида (ЛТ и ПС).

14. Суммарная вероятность принятия ошибочного решения (формула и ее объяснение по рисунку).

, где где p(Si) i=0;1 – априорные (доопытные) вероятности посылки сигналов S1 или S0 в канал связи

15. Когерентный прием (вывод правила оптимального корреляционного приема) и структурная схема приемника.

Для того, чтобы передавался именно сигнал можно выразить системой неравенств:

Устремим

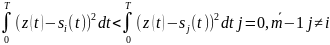
Для двоичного канала связи: (1)

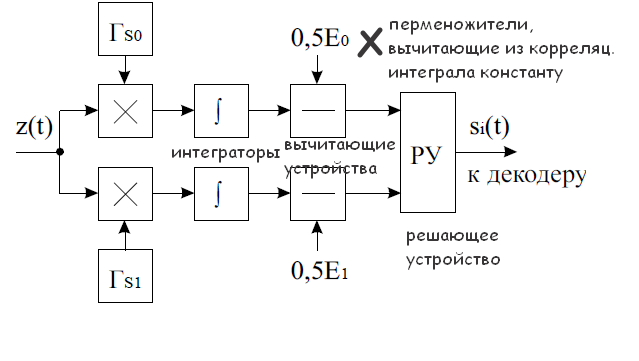Стандартная схема имеет квадраторы, применим эквивалентный метод, не требующий возведения в квадрат. Раскроем скобки и приведем подобные слагаемые:

16. Согласованный фильтр. Принцип работы и структурная схема. Реализация оптимального корреляционного приема на согласованных фильтрах.

Согласованный фильтр (СФ) представляет собой радиотехническое устройство, согласованное с определенной формой сигнала. Это означает, что устройство настроено определенным образом именно на такую форму сигнала. Если теперь подать на вход СФ сигнал этой формы, отклик фильтра будет максимальным в момент времени окончания входного сигнала t=T. Если же на входе СФ действует сигнал любой другой формы (не той, на которую фильтр настроен), то максимум отклика в момент времени t=T будет меньше, чем в первом случае. Таким образом, в этом случае фильтр работает как корреляционный интеграл, т.е. выделяет сигнал, на который настроен, среди всех других.

Рассмотрим условия, при которых СФ будет работать как корреляционный приемник. Корреляционный интеграл:

Если на вход фильтра подать принимаемый сигнал z(t), то напряжение на выходе фильтра y(t):

,

Необходимо выбрать g( ) такой, чтобы в момент окончания входного сигнала z(t=T), напряжение на выходе фильтра y(T) совпадало бы с корреляционным интегралом (1). Тогда фильтр будет осуществлять оптимальный прием сигнала. Это правило будет выполнено, если импульсная характеристика будет симметрична входному сигналу относительно вертикальной оси Т/2

при 0

Реализация оптимального корреляционного приема на согласованных фильтрах