
- •1.Количество информации (логический вывод формулы) и энтропия источника сообщений.
- •2.Условная энтропия (вывод формулы), избыточность и производительность источника сообщений.
- •3.Взаимная информация; информация в непрерывных сигналах и дифференциальная энтропия (вывод формулы для Гауссовского процесса).
- •4.Теорема кодирования для источника сообщений и теорема кодирования для канала с помехами (шумами).
- •5.Пропускная способность дискретного канала связи (вывод формулы).
- •6.Пропускная способность непрерывного канала связи (вывод формулы).
- •7.Эпсилон-энтропия и эпсилон-производительность (вывод формулы)
- •8.Эффективное кодирование. Цель и принцип. Коды Хаффмена и Шеннона-Фано.
- •9.Помехоустойчивое кодирование. Цель и принцип. Основные параметры пу кодов.
- •10.Линейный двоичный блочный код. Кодирование и декодирование. Синдром. Аппаратные средства создания и проверки данного кода.
- •11. Непрерывные помехоустойчивые коды. Сверточный код. Кодирование (схема кодера) и декодирование (решетчатая диаграмма – иметь схему с собой на листочке).
- •17. Потенциальная помехоустойчивость при когерентном приеме (вывод формулы).
- •19. Алгоритм оптимального приема аналогового (непрерывного) сигнала в шумах (Объяснение правила). Корреляционный интеграл. Схема следящего измерителя.
- •20. Помехоустойчивость при оптимальном приеме непрерывных сигналов. Выигрыш (понятие, основная формула).
- •21. Выигрыш при ам (вывод формулы).
- •22. Выигрыш при фм (вывод формулы).
- •23. Выигрыш при чм (вывод формулы).
- •24. Икм. Принцип и основные соотношения. Мощность шумов квантования и ложных импульсов.
- •25. Дикм. Принцип работы и структурная схема.
- •26. Дм. Принцип работы и структурная схема.
- •27. Многоканальная система связи с врк. Принцип и структурная схема.
- •28. Многоканальная система связи с чрк. Принцип и структурная схема.
- •29. Многоканальная система связи с кодовым разделением каналов (по форме сигналов). Принцип, структурная схема и пример используемых сигналов.
- •30. Асинхронно-адресные системы связи. Принцип, преимущества и недостатки, пример используемых сигналов.
5.Пропускная способность дискретного канала связи (вывод формулы).
Пропускная способность канала связи – это максимально возможная скорость передачи информации по каналу связи.
C = Vk‧maxI(A,B)
Найдем пропускную способность дискретного симметричного n-разрядного канала:
 (1)
(1)
Найдем
энтропию шума H(B|A):

Так как канал симметричный, то все
сообщения на его входе появляются с
одинаковой вероятностью. Поэтому
P( )=1/n
)=1/n
При
верной передаче символа i=k:
P( )
= 1–p
)
= 1–p
При ошибочной передаче символа i≠k: P( ) = p/(n–1)
Поскольку на вход канала поступает всего n сообщений, то количество всех случаев ошибочной передачи будет n*(n-1).
Подставим все в формулу энтропии шума и разобьем двойную сумму на случай правильной и неправильной передачи:

H(B)=log(N)
Подставить все в формулу (1)
6.Пропускная способность непрерывного канала связи (вывод формулы).
Найдем пропускную способность непрерывного канала связи:
 (1)
(1)
h(Z|S)
соответствует гауссовскому закону:
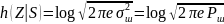 , потому что дисперсия пропорциональная
плотности шума
, потому что дисперсия пропорциональная
плотности шума
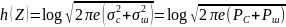
Подставим все в (1):
 =
=
7.Эпсилон-энтропия и эпсилон-производительность (вывод формулы)
Эпсилон-энтропия Hε(B) это то минимальное количество информации, которое необходимо передать по каналу связи чтобы принятый сигнал b*(t) был бы еще эквивалентен переданному b(t).
 (1)
(1)
H(B|A)
соответствует гауссовскому закону:
 ,
где Pε
– это мощность шума воспроизведения
,
где Pε
– это мощность шума воспроизведения
H(B) тоже
подчиняется гауссовскому закону:
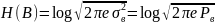 ,
где Pв – мощность сигнала посылаемого
от кодера в канал связи
,
где Pв – мощность сигнала посылаемого
от кодера в канал связи
Подставим в (1) и сократим:

Эпсилон-производительность источника непрерывной информации – это минимальное количество информации, которое необходимо передать за 1 с, чтобы принятый сигнал был еще эквивалентен переданному:
 ,
где Fв - верхняя частота спектра сообщения
,
где Fв - верхняя частота спектра сообщения
8.Эффективное кодирование. Цель и принцип. Коды Хаффмена и Шеннона-Фано.
Эффективное кодирование осуществляется с применением неравномерных кодов, в которых более короткие кодовые комбинации соответствуют более вероятным символам сообщения, а более длинные — менее вероятным символам.
Основными требованиями, предъявляемыми к эффективному коду, являются: 1) однозначность декодирования, т. е. каждому символу кодируемого сообщения должна соответствовать своя кодовая комбинация и для всех символов комбинации должны быть различны; 2) в среднем на один символ сообщения должно приходиться минимальное число элементов кодовой комбинации эффективного кода; 3) ни какая более короткая комбинация эффективного кода не должна являться началом другой, более длинной комбинации.
Цель эффективного кодирования – снижение первоначальной избыточности источника и уменьшение тем самым времени передачи информации. Достигается это за счет неравной вероятности появления сообщений источника.
9.Помехоустойчивое кодирование. Цель и принцип. Основные параметры пу кодов.
Помехоустойчивым (корректирующим) кодированием называется кодирование, при котором осуществляется обнаружение либо обнаружение и исправление ошибок в принятых кодовых комбинациях. Возможность помехоустойчивого кодирования осуществляется на основании теоремы, сформулированной Шенноном.
Основным принципом помехоустойчивого кодирования является использование избыточных кодов, причем если для кодирования сообщения используется простой код, то в него специально вводят избыточность. Необходимость избыточности объясняется тем, что в простых кодах все кодовые комбинации являются разрешенными, поэтому при ошибке в любом из разрядов приведет к появлению другой разрешенной комбинации, и обнаружить ошибку будет невозможно. В избыточных кодах для передачи сообщений используется лишь часть кодовых комбинаций (разрешенные комбинации). Прием запрещенной кодовой комбинации означает ошибку.
Основные понятия и характеристики помехоустойчивых кодов: 1) q (кратность ошибки) – количество ложных импульсов в принятой кодовой комбинации; 2) d(bi, bj) (кодовое расстояние) – расстояние между двумя кодовыми комбинациями; 3) dmin (минимальное кодовое расстояние) – минимальное расстояние среди всех пар кодовых комбинаций данного кода. Если dmin = 1, код считается не помехоустойчивым; 4) кратность исправляемой ошибки qи=(dmin-1)/2 неч и qи=(dmin/2)-1 чет; 5) кратность обнаруживаемой ошибки qо=dmin-1

