1.Количество информации (логический вывод формулы) и энтропия источника сообщений.

Количество информации – это некоторая количественно мера, позволяющая оценивать содержащуюся в сообщении и переносимую сигналом информацию. Свойства: 1) Количество информации – аддитивная величина I(a)=I(a1)+I(a2); 2) Количество информации в сообщении о достоверном событии равно нулю; 3) Количество информации не зависит от качественного содержания сообщения.

P(a) – это вероятность того, что источник сообщений выдает сообщение а. Поскольку P(a)≤1, используют 1/P(a), чтобы значение логарифма было положительным. Основание логарифма может быть любым, но обычно его выбирают равным 2, поскольку для передачи информации в системах связи, как правило, используются двоичные коды.

Энтропия – это количество информации, приходящемся в среднем на одно сообщение источника, т.е. математическое ожидание. Свойство: 1) Энтропия неотрицательна; 2) Энтропия аддитивна; 3) Энтропия максимальна в равновероятных событиях.

2.Условная энтропия (вывод формулы), избыточность и производительность источника сообщений.

Избыточность показывает какая доля от максимально возможной энтропии не передается источником, а могла бы передаваться. Избыточность меняется от нуля, до единицы.

Производительностью (бит/с) источника сообщений H’(A) называют суммарную энтропию сообщений, переданных за единицу времени

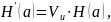где Vu - количество сообщений, выдаваемых источником в секунду.

Условная энтропия H(B|A) – это мера неопределенности ансамбля B при условии, что какое-то из сообщений ансамбля A уже было принято.

Вывод:

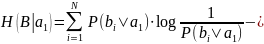зафиксируем ансамбль сообщений А: пусть A=a1, т.е. получатель интерпретирует любое сообщение из ансамбля B как a1. То же самое делаем и для A=a2.

усредним и подставим предыдущее выражение в эту формулу

3.Взаимная информация; информация в непрерывных сигналах и дифференциальная энтропия (вывод формулы для Гауссовского процесса).

Взаимная информация – это количеством информации, содержащейся в В относительно А и наоборот: I(A,B) = H(A)–H(A|B) = H(B) –(B|A), где H(A|B) – это ненадежность канала, а (B|A) – это энтропия шума.

Информация в непрерывных сигналах:

г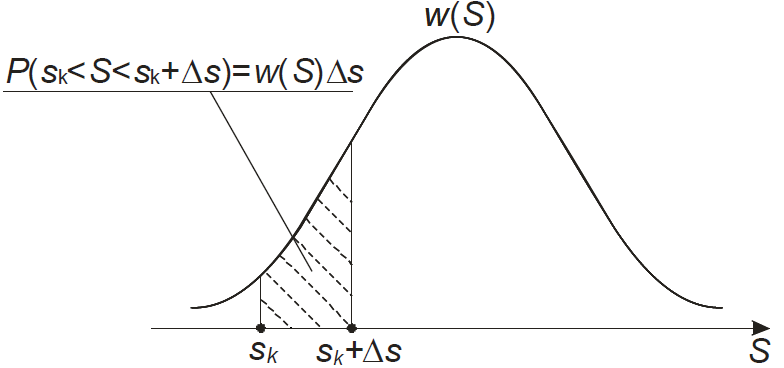 де S – это непрерывная величина, w(S) – е плотность распределения вероятности.

Кол-во информации:

Энтропия:

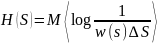
I(S,Z) = h(S)–h(S|Z), где h(S) - дифференциальная энтропия, а h(S|Z) - условная дифференциальная энтропия

Вывод дифференциальной энтропии для гауссовского случайного процесса:

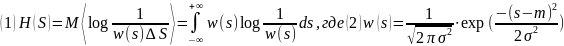
Подставляем (2) в (1) с учетом свойств логарифмов:

4.Теорема кодирования для источника сообщений и теорема кодирования для канала с помехами (шумами).

Теорема кодирования для источника: если количество кодовых символов на одно сообщение Vk/Vu больше энтропии источника то существует способ кодирования, при котором потери информации сводятся к сколь угодно малой величине (практически к нулю). Если же соотношение не выполняется, то такого способа не существует, и потери информации при кодировании неизбежны.

Теорема кодирования для канала с помехами: если производительность источника сообщений H’(A) меньше пропускной способности канала H’(A) < С, то существует способ кодирования (преобразования сообщения в сигнал) и декодирования (преобразования сигнала в сообщение), при котором вероятность ошибочного декодирования и ненадежность канала H(A|B) могут быть сколь угодно малы. Если же H’(A) > С, то таких способов кодирования и декодирования не существует.