
- •2. Состав электрической цепи и схема ее замещения
- •3. Пассивные элементы цепи
- •4. Топологические параметры схем цепей:
- •5. Активные элементы цепей
- •5А. Независимый источник напряжения и его характеристики
- •5Б. Независимый источник тока и его характеристики
- •6. Взаимные преобразования источников энергии
- •7. Законы Ома и Кирхгофа
3. Пассивные элементы цепи
 Пассивными
называют
элементы, которые не могут генерировать
электрическую энергию. К
пассивным элементам относят:
резисторы,
индуктивные катушки и
конденсаторы (рис.
1.3).
Пассивными
называют
элементы, которые не могут генерировать
электрическую энергию. К
пассивным элементам относят:
резисторы,
индуктивные катушки и
конденсаторы (рис.
1.3).
Резистор – пассивный элемент электрической цепи, предназначенный для использования его электрического сопротивления R (Ом).
У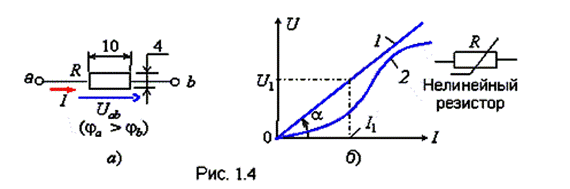 словное
графическое обозначение линейного
резистора на схеме цепи показано на
рис. 1.4а.
словное
графическое обозначение линейного
резистора на схеме цепи показано на
рис. 1.4а.
Основной параметр резистора – его сопротивление. Электрическое сопротивление постоянному току – скалярная величина R, равная отношению постоянного напряжения между выводами пассивного двухполюсника к постоянному электрическому току в нём, т.е.
![]()
Зависимость электрического напряжения на выводах пассивного элемента электрической цепи от электрического тока в нём называют уравнением данного элемента или компонентным уравнением. На рис. 1.4б представлены вольтамперные характеристики (ВАХ) линейного (1) и нелинейного (2) резисторов.
Связь тока IR с напряжением UR отображает закон Ома для участка цепи с резистором R:
![]()
UR = RIR или
Мощность (Вт) преобразования электрической энергии в резисторе в тепловую равна
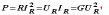
где G = 1/R – электрическая проводимость (в дальнейшем – проводимость) резистора в сименсах (См).
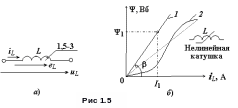 Индуктивная
катушка −
пассивный
элемент цепи, предназначенный для
использования его собственной
индуктивности L
и/или его магнитного поля.
Условные графические обозначения
линейного и нелинейного индуктивных
элементов на схеме цепи показаны на
рис. 1.5а,
б.
Индуктивная
катушка −
пассивный
элемент цепи, предназначенный для
использования его собственной
индуктивности L
и/или его магнитного поля.
Условные графические обозначения
линейного и нелинейного индуктивных
элементов на схеме цепи показаны на
рис. 1.5а,
б.
При нарастании тока в индуктивной катушке происходит преобразование электрической энергии в магнитную и её накопление в магнитном поле катушки, а при убывании тока – обратное преобразование энергии магнитного поля в электрическую энергию, возвращаемую источнику.
Энергия в джоулях (Дж), запасённая в магнитном поле катушки,
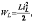
где L – индуктивность катушки; iL – ток, протекающий через катушку и создающий в ней магнитный поток Ф и потокосцепление Ψ в веберах (Вб), равное
Ψ = wФ,
где w – число витков катушки (предполагается, что магнитный поток Ф пронизывает все витки катушки).
Потокосцепление и ток в линейной катушке (см. вебер-амперную характеристику 1 на рис. 1.5б) пропорциональны и связаны соотношением Ψ = Li или
L = Ψ/i.
Откуда единица основного параметра катушки – индуктивности
[ L] = [Ψ] / [I] = В·t / A = Ом·c = Гн (генри).
Согласно закону электромагнитной индукции при изменении потокосцепления в катушке индуктируется ЭДС самоиндукции, равная (при её эксплуатации на линейном участке вебер-амперной характеристики)
eL = – dΨ/dt = – LdiL/dt.
Знак "минус" показывает, что ЭДС самоиндукции, согласно правилу Ленца, препятствует изменению в ней тока. В индуктивной катушке будет протекать ток, если напряжение uL на её зажимах компенсирует ЭДС eL и падение напряжения на электрическом сопротивлении R провода катушки.
Пренебрегая активным сопротивлением R (uL = - eL + RiL ≈ – eL), получим компонентное уравнение идеального индуктивного элемента (катушки):
![]() eL
=
LdiL/dt
и
eL
=
LdiL/dt
и
Условные положительные направления ЭДС самоиндукции eL и напряжения uL на схемах всегда совпадают (см. рис. 1.5а), а направление тока iL произвольное (обычно выбирают направление тока iL, совпадающее с направлением напряжения uL).
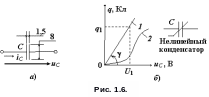
Конденсатор – пассивный элемент цепи, предназначенный для использования его электрической ёмкости С. Условное графическое обозначение линейного ёмкостного элемента на схеме цепи показано на рис. 1.6а.
 При
нарастании напряжения на зажимах
конденсатора в нём происходит
преобразование
электрической энергии внешнего источника
в энергию электрического поля за
счёт накопления зарядов противоположных
знаков на двух его электродах (пластинах).
При
нарастании напряжения на зажимах
конденсатора в нём происходит
преобразование
электрической энергии внешнего источника
в энергию электрического поля за
счёт накопления зарядов противоположных
знаков на двух его электродах (пластинах).
При уменьшении напряжения происходит обратное преобразование энергии электрического поля конденсатора в электрическую энергию, возвращаемую источнику.
Энергия, запасаемая в электрическом поле конденсатора,
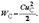
где С – ёмкость (основной параметр конденсатора), определяемая из кулон-вольтной характеристики 1 (линейного) или 2 (нелинейного) конденсаторов (рис. 1.6б).
Накопленный заряд q на одном из электродов линейного конденсатора пропорционален приложенному к его зажимам напряжению uC
q = CuC, а ёмкость С = q/uC,
Откуда единица ёмкости
[C] = [q] / [U] = Кл / В = А·с / В = с / Ом = Ф (фарад).
При изменении напряжения uC накопленные в конденсаторе заряды перераспределяются, вызывая появление тока
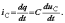
 Итак,
компонентное
уравнение
ёмкостного элемента (незаряженного
конденсатора):
Итак,
компонентное
уравнение
ёмкостного элемента (незаряженного
конденсатора):
