
Поверхности на базе точек. Nurbs-поверхности
Исходная информация для построения уравнения поверхности представляет собой совокупность характеристических точек. Эти точки являются вершинами многогранника, ребра которого образуют сетку, составленную из характеристических ломаных. Множество ломаных условно разбивается на два подмножества: образующих и направляющих. При этом ломаные, принадлежащие одному подмножеству, не имеют общих точек. Переход от одной ломаной к другой на подмножестве образующих характеризуется параметром v ,на подмножестве направляющих - параметром w.
Пример. На рисунке 3.35 показана NURBS-поверхность третьего порядка по каждому из двух направлений. Характеристический многогранник изображен тонкими линиями.

Рисунок 3.35 - NURBS-Поверхность
Поверхности на базе кривых
Пусть задана кривая в параметрической форме f(v) – образующая поверхности. Перемещением этой кривой по направляющей g(w) (рисунок 3.36) можно получить поверхность.
Образующая и направляющая заданы в глобальной системе координат xyz. За базовую кривую при построении поверхности примем направляющую. Введем местную подвижную систему координат, связанную с направляющей g(w) и определяемую единичными ортогональными векторами i1,i2,i3.

Рисунок 3.36 - Образующая и направляющая
Центр местной системы координат лежит на направляющей и определяется параметром w. Пусть направление одной из осей (i3) совпадает с направлением касательной к g(w) в точке w. Для построения поверхности перемещаем образующую таким образом, чтобы положение кривой относительно местной системы координат стало таким же, каким оно было относительно глобальной системы.
Изменение параметра w приводит к перемещению местной системы координат вместе с образующей и позволяет получить непрерывный ряд образующих, задающих поверхность. Поверхность, полученную описанным способом, называют поверхностью заметания (рисунок 3.37).

Рисунок 3.37 - Незамкнутая поверхность заметания
Если перемещать кривую f(v) вдоль направляющей g(w) без поворота, то получим поверхность сдвига (рисунок 3.38).
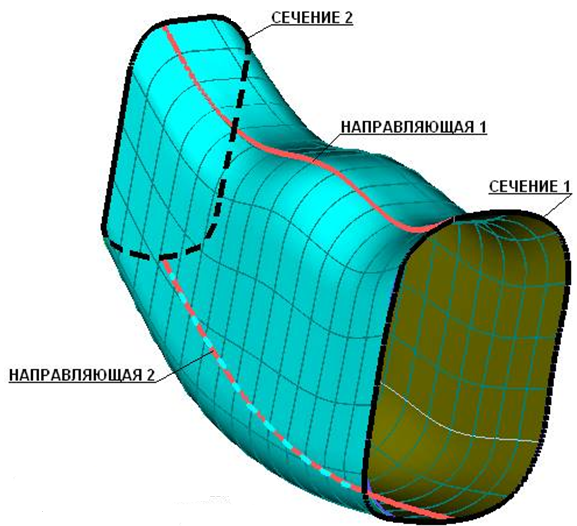
Рисунок 3.38 - Поверхность сдвига по подобным сечениям
Поверхности на базе поверхностей
Эквидистантная поверхность строится по заданной базовой поверхности (рисунок 3.39).

Рисунок 3.39 - Эквидистантная поверхность
Вопросы для самоконтроля
1.Перечислите основные группы функций (5) моделирования твёрдого тела.
2.В чём суть функций создания примитивов и булевых операторов?
3.В чём суть функций заметания, качания (вращения) и скининга?
4.В чём суть функций скругления (плавного сопряжения) и поднятия?
5.В чём суть функций моделирования границ?
6.В чём суть функций объектно-ориентированного моделирования?
7.Какие линии называют кривыми?
8.Перечислите кривые, получаемые сечением плоскостью поверхности конуса. Условия их образования.
9.Как формируется цилиндрическая винтовая линия?
10.В чём суть плазового - шаблонного метода моделирования поверхностей?
11.В чём состоят методы интерполяци и аппроксимации кривых? Чем они отличаются?
12.Приведите пример интерполяции (полином Лагранжа). В чём его недостатки?
13.Объясните суть аппроксимации (интерполяции) массива точек сплайнами.
14.Перечислите методы конструирования кривых линий и поверхностей. Какой подход при этом используют?
15.Сравните формы построения кривых (Эрмита, Безье, В-сплайна). Приведите графические примеры.
16.В чём преимущества и суть построения сплайнов и поверхностей Безье (в том числе составных)?
17.В чём отличие NURBS от В-сплайнов? Перечислите преимущества NURBS.
18.Перечислите классы (4) задания поверхностей в компьютерной графике. Приведите примеры.
