Сравнение форм Эрмита, Безье и b-сплайнов

Каждое из этих представлений оказывается полезным в разных ситуациях. Форма Эрмита пригодна для аппроксимации уже имеющихся поверхностей, когда необходимо добиться как соответствия точек, так и соответствия касательных векторов, в то время как представление в виде B-сплайнов удобно для аппроксимации точек.

Формы Безье и B-сплайнов пригодны для работы в интерактивном режиме, так как их геометрические векторы состоят из одних только точек. Обе эти формы обладают свойством выпуклой оболочки, которое оказывается полезным при изображении кривых. Отметим, что кривую, первоначально заданную в одной форме, можно преобразовать в другую форму.

На рисунке 3.28 и рисунке 3.29 показано различие в поведении кривых, построенных разными методами на основе одного и того же точечного базиса.

Рисунок 3.28 - Три формы построения кривых: а – форма Эрмита;

б – форма Безье; в – форма В-сплайна

Рисунок 3.29 - Сглаживание фигуры: а – исходная фигура;

б – форма В-сплайна; в – форма Безье; г – форма Эрмита

Одними из самых популярных сплайнов, применяемых в компьютерном моделировании, являются "кривые Безье" и NURBS-кривые (Non-Uniform Rational B-Spline - неоднородный рациональный фундаментальный сплайн). Эти сплайны обладают высокой степенью гладкости, легко вычисляются и управляются.

Кривая (сплайн) Безье задаётся вершинами многоугольника и в общем случае не проходит через базовые точки (рисунок 3.30).

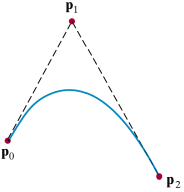
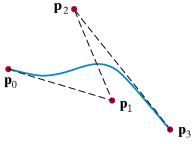
Рисунок 3.30 - Сплайны Безье

Для получения кривой, проходящей через заданные точки применяются составные кривые Безье, которые также можно использовать для задач интерполяции.

Поверхности Безье используются при интерактивном проектировании по тем же причинам, что и кривые Безье: управляющие точки позволяют легко изменять форму куска поверхности. Поверхности Безье так же, как и кривые Безье, обладают свойством выпуклой оболочки. Геометрическая матрица состоит из 16 управляющих точек (рисунок 3.31).

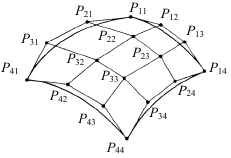
Рисунок 3.31 - Шестнадцать управляющих точек бикубического куска Безье

Для достижения непрерывности в поперечном направлении относительно ребер кусков необходимо равенство четырех управляющих точек, принадлежащих общим ребрам соседних кусков. Для непрерывности касательного вектора требуется, чтобы две четверки управляющих точек по обеим сторонам общего ребра были коллинеарны другим ребрам. Коллинеарными будут следующие совокупности управляющих точек: (P13, P14, P15), (P23, P24, P25), (P33, P34, P35), (P43, P44, P45). Отношения длин коллинеарных отрезков должны быть постоянными (рисунок 3.32).

Рисунок 3.32 - Составные поверхности Безье

На рисунках 3.33 и 3.34 приведены примеры B-сплайновых поверхностей.

Рисунок 3.33 - Пример В-сплайновой поверхности

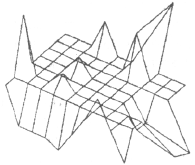
Рисунок 3.34 - Каркас и В-сплайновая поверхность

Неоднородный рациональный В-сплайн или NURBS подобен обычному неоднородному В-сплайну.

NURBS-кривые не проходят через базовые точки, а усредняют - аппроксимируют их, причём узловые точки могут быть расставлены неравномерно. Такие линии называются неоднородными, а каждый такой узел, имеющий свой вес (коэффициент, определяющий влияние данной точки на кривизну линии), - рациональным. Перемещая узловые точки, можно управлять формой кривой (рисунок 3.35).

Рисунок 3.35 - Интерактивное управление формой гладких NURBS-кривых

NURBS позволяет точно воспроизвести все конические сечения - окружность (см. рисунок 3.35 справа), эллипс, параболу и гиперболу. В NURBS - представлении можно работать не только с коническими сечениями, но с кривыми Безье, рациональными кривыми Безье и В-сплайнами. Преобразование всех этих кривых к NURBS может значительно сократить объем программирования.

Задание поверхностей в компьютерной графике

Поверхность может быть задана различными способами, которые можно свести к четырем классам: аналитическое задание, задание на базе точек, на базе линий и на базе поверхностей. Далее рассмотрены несколько примеров, характерных для каждого из перечисленных классов.

Аналитическое описание

Эта форма записи наиболее удобна для моделирования, поскольку позволяет точно определить любую точку поверхности, выполнять преобразования поверхности и проводить расчеты.

Для аналитического представления поверхности необходимо записать уравнение поверхности в выбранной системе координат. Чаще всего применяют описания поверхности в прямоугольной системе координат, которое в общем виде записывают следующим образом f(x,y,z)=0.

Например:

- уравнение плоскости - a₁x+a₂y+a₃z+a₄=0.

Поверхности второго порядка можно описать каноническими уравнениями:

- эллипсоид -

- однополостный гиперболоид -

- эллиптический параболоид -

Эти уравнения справедливы только при определенном выборе направления осей и начала координат (например, оси координат должны совпадать с осями эллипсоида).

В некоторых случаях удобно представлять уравнение поверхности в параметрическом виде.