Добавил:

AnonimusPro Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технологический университет "Станкин"

Предмет:

Физика

Файл:

Семинар 1 Механика

.pdf

Скачиваний:

Добавлен:

10.01.2021

Размер:

300.12 Кб

Скачать

☆

Семинар №1

Динамика материальной точки

В классической нерелятивистской механике, где скорость движения тел считается много меньше скорости света в вакууме c 3 108 м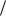с , основным законом динамики является II-ой закон Ньютона. Согласно этому закону в

инерциальной системе отсчета первая производная импульса тела по

времени t			равна полной силе				, действующей на это тело,
времени t			равна полной силе			F	, действующей на это тело,
								(1.0.1)
					dp F .			(1.0.1)

					dt
Здесь								dt - мгновенная скорость тела,
Здесь		p m		, m – инертная масса тела, dr				dt - мгновенная скорость тела,
	-	радиус-вектор тела,				определяющий		его положение в выбранной
r (t)	-	радиус-вектор тела,				определяющий		его положение в выбранной

инерциальной системе отсчета.

При определении мгновенной скорости тела рассматривается как материальная точка, т.е. линейные размеры тела считаются малыми по сравнению с характерными расстояниями решаемой задачи и не учитывается вращательное движение тела.

Если масса тела m при движении сохраняется постоянной, уравнение (1.0.1)упрощается и принимает вид

d 2 r

(m ) m

(1.0.2)

где

- мгновенное

ускорение

тела.

Это

обыкновенное

d 2 r dt 2

дифференциальное уравнение второго порядка по времени. Для однозначного определения решения уравнение (1.0.2), т.е. нахождения

					t t0
функции	r (t) , необходимо в некоторый момент времени				t t0	задать два
начальных условия:
				,			.
	r	r0		,		0	.
(1.0.3)		t t0				t t0
(1.0.3)
В этом случае при заданной силе				все последующие состояния тела
В этом случае при заданной силе			F	все последующие состояния тела			r (t) ,

	для t t0	находятся однозначно.
(t)

Определение движения тела по заданным начальным условиям и известной силе называется прямой задачей динамики. В обратной задаче требуется найти силу, которая обеспечивает необходимые характеристики движения тела (это задача управления движением тела).

Задача № 1

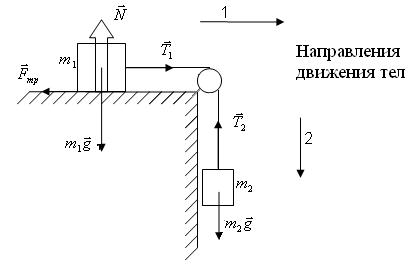
Два тела с массами m1 и m2 связаны между собой нерастяжимой и невесомой ( m 0 ) нитью, перекинутой через невесомый блок. Коэффициенты трения скольжения между телом 1 и горизонтальной поверхностью 0,2.

Ускорение свободного падения g 9,8 м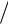с2 . Блок считается невесомым. Трением в блоке можно пренебречь. Определить ускорения тел a1 и a2 , если

в начальный момент времени t 0	они были неподвижны. Рассмотреть два
случая: 1) m1 10кг, m2 5кг ;	2) m1 10кг, m2 1кг .

Решение Это прямая задача динамики, где по заданным действующим силам

необходимо рассчитать движение тел в системе с кинематическими связями. Решение задачи выполняется с помощью следующего алгоритма.

1. Укажем все силы, которые согласно условиям задачи действуют на тела системы с отличной от нуля массой (движение невесомых тел определяется


связями): силы тяжести		m g	и	m g ,	силы натяжения	T	и	T	, сила реакции
		1		2		1		2
опоры N , сила трения	Fтр .
2. Согласно II-ому закону Ньютона запишем в векторной форме уравнения
движения тел 1 и 2:

	m1a1 T1			m1g	N Fтр ,				(1.1.1)

	m2a2		T2 m2 g .						(1.1.2)

3. Поскольку тела движутся вдоль прямых, то удобно перейти от векторных уравнений к одномерным скалярным уравнениям, используя проекции уравнений (1.1.1)-( 1.1.2) на направления соответствующих движений:

m1a1 T1 Fтр ,	(1.1.3)
0 m1 g N ,	(1.1.4)
m2 a2 m2 g T2 .	(1.1.5)
В полученные 3 уравнения входят 6 неизвестных величин:	a1 , a2 ,T1 ,T2 , N и

Fтр . Для однозначного нахождения всех 6 неизвестных систему уравнений

(1.1.3)-(1.1.5) необходимо дополнить еще тремя независимыми уравнениями. 4. Для получения дополнительных уравнений воспользуемся условиями задачи и законами физики.

Поскольку нить нерастяжима, то величины ускорений должны быть одинаковыми

a1 a2 a 0 .

(1.1.6)

Нить и блок считаются невесомыми, трение в блоке не учитывается, поэтому величины сил натяжения равны друг другу во всех точках нити

T1 T2 T .

(1.1.7)

Сила трения имеет различную физическую природу и величину в зависимости от того, движется тело 1 относительно поверхности или нет:

Fтр	Fтр.п. (тело 1 неподвижно) ,
Fтр	Fтр.ск. (тело 1 движется) .	(1.1.8)

Здесь Fтр.п. – сила трения покоя и Fтр.ск. – сила трения скольжения.

В зависимости от условий задачи возможны два решения.

I. Допустим, что действующие силы обеспечивают движение тел и

Fтр Fтр.ск. N .

В этом случае полная система уравнений принимает вид: m1a T N ,

0 m1g N , m2a m2 g T .

Решая эту систему равнений, получим:

a m2 m1 g, m1 m2

T (1 )	m1m2		g,
	m m	2
1
N m1g .

Данное решение справедливо, если a 0 или m2 m1 .

(1.1.9)

(1.1.10)

(1.1.11)

(1.1.12)

(1.1.13)

(1.1.14)

(1.1.15)

Физический смысл последнего условия заключается в том, что сила тяжести m2 g , действующая на тело 2, должна превышать максимальное значение силы трения покоя Fтр.п. Fтр.ск. N m1g , действующей на

тело 2 и препятствующей движению.
II. Если m2 m1 , тела остаются в состоянии покоя и
Fтр Fтр.п. .	(1.1.16)
Соответствующая полная система уравнений принимает	вид (
a1 a2 0 ):
0 T Fтр.п. ,	(1.1.17)
0 m1g N ,	(1.1.18)

0 m2 g T .

(1.1.19)

Решение этой системы дает:

T Fтр.п. m2 g ,

(1.1.20)

N m1g .

Для m1 10кг , m2 5кг и

0,2 справедливо условие m2 m1 ,

поэтому тела движутся с ускорением

a a

g 1,96 м с2

(1.1.21)

При m1 10кг , m2 1кг и 0,2 выполняется условие m2

m1 , сила

трения покоя Fтр.п. m2 g и тела остаются в состоянии покоя

a1 a2 0 .

(1.1.21)

Ответ: 1)

a1 a2

m2 m1

g 1,96 м с2 ; 2) a1

a2 0 .

m1 m2

Задача №2

На

краю горизонтального

диска радиусом

R 0,1м

неподвижно

лежит маленькая шайба. В момент времени t 0 диск начинает вращаться вокруг вертикальной оси, проходящей через его центр, с угловым

ускорением 1 рад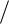с2 . Через какое время t1 шайба соскользнет с диска, если коэффициент скольжения между шайбой и поверхностью диска

0,2 ?

Угловая скорость и угловое ускорение определяются следующим образом

d	,	d	d 2	,	(1.2.1)
dt		dt	2
			dt

где - угол поворота диска вокруг вертикальной оси.

Шайба

совершает

ускоренное движение

по

окружности, где

еѐ

удобно представить в виде векторной суммы.

ускорение a

an .

(1.2.2)

Здесь

–

тангенциальное

ускорение,

направленное

по касательной

окружности

(1.2.3)

- единичный

вектор

касательной

окружности,

направленный

по

где

вектору

скорости

Это

ускорение

определяет

скорость

изменения

величины

скорости

Ускорение

–

нормальное

ускорение,

перпендикулярное к касательной окружности в точке нахождения шайбы и направленное к центру окружности

	2
an	R		n .	(1.2.4)
	R
Единичный вектор нормали		перпендикулярен к вектору
Единичный вектор нормали	n	перпендикулярен к вектору		и направлен к

центру окружности. Нормальное ускорение определяет скорость изменения

направления направление .

Решение Это пример обратной задачи динамики, где по заданному ускорению

тела требуется найти необходимую силу.

1. Определим все силы, которые действуют на шайбу согласно условиям

задачи: сила тяжести		, сила реакции опоры		и сила трения покоя
	mg		N		Fтр.п.

(шайба считается неподвижной относительно поверхности диска).

2. Запишем в векторной форме уравнение движения шайбы в лабораторной системе отсчета


	ma	mg	N Fтр.п. .			(1.2.5)
Поскольку ускорение шайбы в вертикальном направлении равно нулю, то

	mg	N 0				(1.2.6)
и уравнение (1.2.5) упрощается

	ma	Fтр.п. .				(1.2.7)

Используя разложение полного ускорения шайбы на тангенциальное a и

нормальное an	ускорения, запишем уравнение (1.2.7) в виде
			m an
	m a F ,		m an	Fn ,		(1.2.8)

где Fтр.п. Fn F .
3. Перейдем от векторной формы записи уравнения						(1.2.8) к скалярной,

используя проекции на направления ускорений an					и a	,
	ma	F ,	man	Fn .		(1.2.9)

4. Определим зависимость величины полного ускорения шайбы

a2 an2

(1.2.10)

от времени. Согласно определению

a	d	d	( R) R	d	R .	(1.2.11)
	dt	dt		dt

Здесь использована известная формула для линейной скорости материальной точки, движущейся по окружности, R . Нормальное ускорение определяется выражением

an	2	2 R2
an		2 R	,
	R	R
(1.2.12)

в которое входит неизвестная угловая скорость (t) . Для нахождения (t) используем определение углового ускорения

	d
	dt .	(1.2.13)

Разделим в этом дифференциальном уравнении относительно угловой скорости переменные и t

dt d	(1.2.14)
и проинтегрируем левую часть по времени от t 0	до текущего момента

времени t , а правую часть по угловой скорости от начального значения 0 до текущего значения (t)

t	(t )
dt	d .	(1.2.15)
0	0
Выполняя интегрирование
t t		(1.2.16)
и подставляя (1.2.16) в (1.2.10), найдем, что
an (t) 2 Rt 2 .		(1.2.17)
Из (1.2.10), (1.2.11) и (1.2.17) следует, что величина полного ускорения

a(t)	R2 2 R2 4t 2	(1.2.18)

монотонно растет со временем.

5. В соответствии с ростом величины ускорения должна расти сила трения покоя, обеспечивающая это ускорение,


Fтр.п. ma(t) m R2 2 R2 4t 2 .			(1.2.19)

Однако величина силы трения покоя ограничена сверху величиной силы трения скольжения Fтр.ск. N mg

Fтр.п. mg ,		(1.2.20)
поэтому условие движения шайбы вместе с диском принимает вид

m R2 2 R2 4t 2	mg .	(1.2.21)

Отсюда находим, что в момент времени t1 , когда

		m R2 2 R2 4t12		mg ,			(1.2.22)
шайба слетит с диска. Таким образом,

		t 4	2 g 2 R2 2		4,5с.		(1.2.23)
		1	4 R2				(1.2.23)
Отметим, что при		g R шайба слетит с диска				сразу после начала
вращения.
Ответ: t1 4,5с.
			Задача №3
Автомобиль		массой	m 2000кг движется			прямолинейно со
скоростью	0 72 км ч . В		момент времени t 0			на него	начинает
действовать	тормозящая сила, линейно растущая со					временем	согласно

формуле Fт t , где 103 Н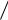с . Определите время t1 , необходимое

для полной остановки автомобиля, и соответствующий тормозной путь S1 . Решение

Это прямая задача механики, где по заданной силе необходимо определить движение тела.

1. При t 0 на автомобиль действует единственная горизонтальная сила

Fт , направленная против вектора скорости автомобиля. Векторное уравнение движения автомобиля в горизонтальной плоскости запишется

следующим образом:

m d		F

		т .				(1.3.1)
	dt	т .				(1.3.1)
	dt
2. Перейдем к скалярной форме				записи с		помощью проекции

уравнения (1.3.1) на направление вектора скорости						:
m	d	F	t		.	(1.3.2)
m		F	t
	dt	т
	dt

Это обыкновенное дифференциальное уравнение первого порядка по времени относительно неизвестной функции .

3. Дифференциальное уравнение (1.3.2) решается методом разделения переменных и t :

d	tdt .	(1.3.3)
	m

Проинтегрируем левую часть по скорости от еѐ начального значения 0 до текущей величины (t ) , а правую часть по времени от начального момента t 0 до текущего момента времени t

(t )	t	tdt		t
d				tdt .
0	0	m	m	0

Выполняя интегрирование, получим

(t) 0 t 2 m 2

или

(t) 0 t 2 . m 2

4. В момент остановки автомобиля t t1

(t1 ) 0 ,

поэтому из (1.3.6) находим, что

(1.3.4)

(1.3.5)

(1.3.6)

(1.3.7)

t	2m 0	8,94с	.	(1.3.8)

1

5. Тормозной путь S1 находится с помощью определения величины скорости для прямолинейного движения

S1 dS S1

dSdt , dS dt,

t1 t1

dt ( 0

0t1

t 2 )dt m 2

t13 2

2m 3 3 0

Ответ: t1 8,94с ; S1 119м .

(1.3.9)

(1.3.10)

t1 t 2

m 2

t 2 dt

2m 0

119м.

(1.3.11)

Соседние файлы в предмете Физика

#
10.01.20217.63 Mб69Презентация термодинамика и статистич физика Лекция 2.ppt
#
10.01.202120.39 Mб31Презентация термодинамика и статистич физика Лекция 4.ppt
#
10.01.202134.1 Mб31Презентация термодинамика и статистич физика Лекция 5..ppt
#
10.01.20211.74 Mб38Презентация термодинамика и статистич физика Лекция 6..ppt
#
10.01.202148.75 Mб27Презентация термодинамика и статистич физика Лекция 7..ppt
#
10.01.2021300.12 Кб5Семинар 1 Механика.pdf
#
10.01.2021281.25 Кб10Семинар 1. Термодинамика.pdf
#
10.01.2021277.17 Кб9Семинар 2 Механика.pdf
#
10.01.2021218.42 Кб7Семинар 2. Термодинамика.pdf
#
10.01.2021313.57 Кб4Семинар 3 Механика.pdf
#
10.01.2021208.42 Кб8Семинар 3. Уравнение Ван-дер-Ваальса.pdf