- •Термодинамика и статистическая физика
- •Лекция № 2
- •Внутренняя энергия
- •В термодинамике важно знать не абсолютное значение внутренней энергии,
- •Внутренняя энергия U одного моля идеального одноатомного газа равна:
- •В каждом состоянии система обладает
- •Внутренняя энергия U ν молей
- •Работа и теплота
- •Работа, совершаемая системой при бесконечно
- •РАБОТА ПРИ
- •РАБОТА – ХАРАКТЕРИСТИКА ПРОЦЕССА
- •Количество теплоты Q , представляет собой энергию, которая передаётся от одного тела к
- •Первое начало термодинамики
- •Закон сохранения энергии для
- •Теплота Q и работа А зависят от того, каким образом совершен переход из
- •Теплотой называется энергия, передаваемая от тела с более высокой температурой телу с мень-
- •Если идеальный газ, получив теплоту,
- •Особое значение в термодинамике имеют круговые или циклические процессы, при которых система, пройдя
- •Цикл, совершаемый идеальным газом, можно разбить на
- •Если за цикл совершается положительная работа
- •Прямой цикл
- •Прямой цикл используется в тепловых двигателях – периодически действующих установках, совершающих работу за
- •Термический коэффициент полезного действия ( КПД ) для кругового процесса:
- •Термический процесс называется обратимым, если он может происходить как в прямом, так и
- •Реальные процессы сопровождаются диссипацией энергии (из-за трения, теплопроводности и т.д.) и являются необратимыми.
- •При адиабатическом расширении газа условие теплоизолированности системы исключает непосредственный теплообмен между системой и
- •Тепловые машины
- •Любая тепловая машина работает по принципу кругового (циклического) процесса, т.е. возвращается в исходное
- •Но чтобы при этом была совершена полезная работа, возврат должен быть произведен с
- •Принцип действия тепловых двигателей
- •Зачем холодильник? Так как в тепловой машине реализуется круговой процесс, то вернуться в
- •Прямой цикл используется в
- •От термостата с более высокой температурой Т1, называемого
- •КПД тепловых двигателей
- •КПД тепловых двигателей
- •КПД тепловых двигателей
- •КПД тепловых двигателей
- •КПД тепловых двигателей
- •Обратный цикл используется в холодильных машинах –
- •Цикл Карно (обратимый).
- •Карно Никола Леонард Сади
- •Цикл Карно является самым экономичным и представляет собой круговой процесс, состоящий из двух
- •ТЕОРЕМА КАРНО
- •Количество теплоты Q2 , отданное газом холодильнику при изотермическом сжатии, равно работе сжатия
- •Термический КПД цикла Карно:
- •Холодильная машина
- •Обратный цикл Карно
- •Холодильный коэффициент К для холодильных машин Карно:
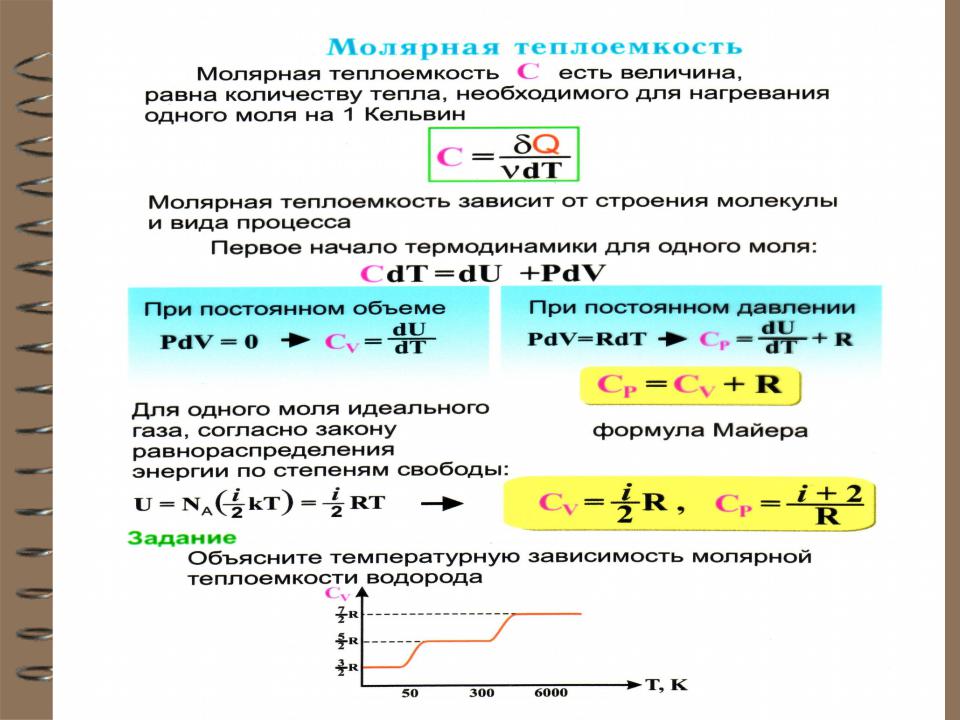
- •Теплоёмкость идеального газа
- •Удельная теплоёмкость Суд – есть
- •Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании.
- •СР – теплоемкость
- •Следовательно, проводимое тепло затрачивается и на нагревание и на совершение работы. Отсюда ясно,
- •При изобарическом процессе кроме увеличения внутренней энергии происходит совершение работы газом (из I
- •В общем случае C
- •Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V,
- •Внутренняя энергия одного моля идеального одноатомного газа равна: U NA 32 kT 32
- •Внутренняя энергия одного моля идеального газа c i степенями свободы равна:
- •Учитывая физический смысл R для изобарических процессов можно записать:
- •Для одного моля идеального газа:
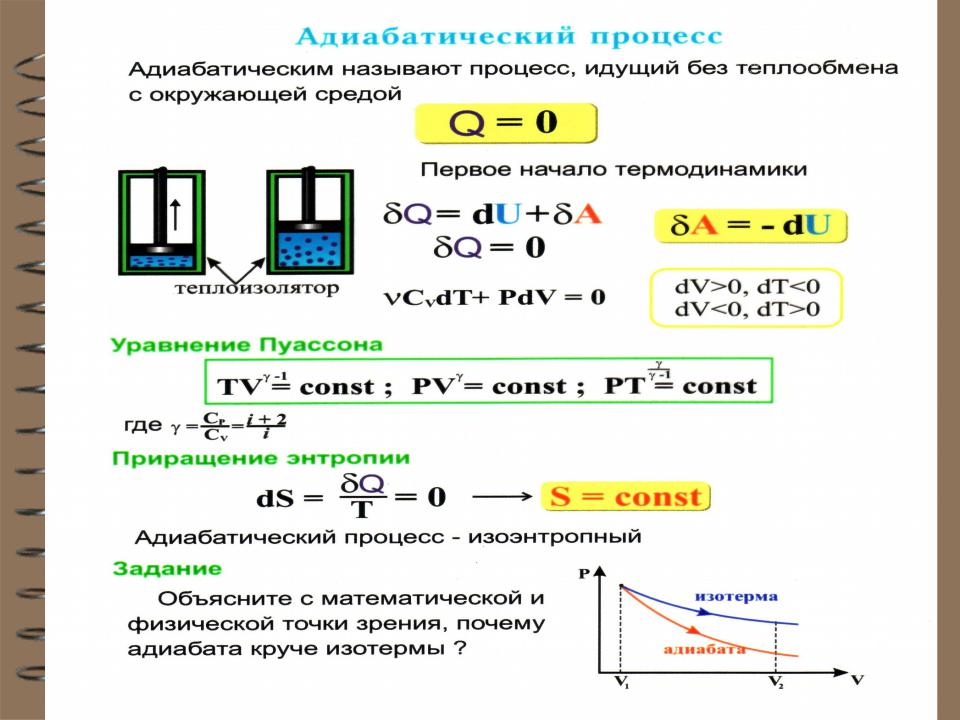
- •Адиабатный (адиабатический) процесс
- •Здесь уместно рассмотреть еще и
- •С помощью показателя n можно легко описать любой изопроцесс:
- •ИЗОПРОЦЕССЫ
- •ЛЕКЦИЯ ЗАКОНЧЕНА!

В общем случае C |
U |
|
|
|
|
V |
|
|
|
|
T V |
так как внутренняя энергия U может зависеть
только от температуры.
В случае 1 моля идеального газа спра- ведлива формула изм. внутренней энергии:
dUμ CV dT
Из этого следует, что для 1 моля:
T |
|
Uμ CV dT CVT |
Uμ CVT |
0

Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р и тому подобных величин), поэтому формула
U CV T справедлива для любого процесса ( для 1 моля).
Для произвольной массы идеального
газа: m
U CV T

Внутренняя энергия одного моля идеального одноатомного газа равна: U NA 32 kT 32 RT
U 32 RT
dU |
|
3 |
R 12,5 |
Дж |
, |
||
CV |
|
|
|
|
|||
2 |
моль К |
||||||
|
dT V |
|
|
|
|||
- молярная |
|
теплоемкость при |
|||||
постоянном объеме СV – величина постоянная, от температуры не зависит.

Внутренняя энергия одного моля идеального газа c i степенями свободы равна:
U 2i RT
dU |
|
i |
|
||
CV |
|
|
|
R |
|
2 |
|||||
|
dT V |
|
|
||
молярная теплоемкость при постоянном объеме СV – величина
постоянная, от температуры не зависит.

Учитывая физический смысл R для изобарических процессов можно записать:
dQP dUμ RdT
(для одного моля). Отсюда для одноатомного:
Тогда, |
CP 3 R R 5 R |
|
2 |
2 |
|
молярная теплоемкость при |
||
постоянном давлении для одноатомных газов:
CP 5 R 20,8 |
Дж |
|
моль К |
||
2 |
Для одного моля идеального газа:
CP 2i R R i 22 R
Постоянная адиабаты (коэффициент Пуассона) для идеального
газа: |
С |
Р |
i 2 |
|
|
С |
i |
||
|
|
|
||
|
V |
|
|
|
Для одноатомного идеаль-
ного газа (i = 3): 20,8 1,67
12,5

Адиабатный (адиабатический) процесс |
Это процесс, происходящий без теплообмена с окружающей средой, т.е. Q 0
При адиабатном процессе работа системы (или над системой) совершается за счет изме- нения внутренней энергии газа: dU A 0
(из I начала ТД: |
Q dU A |
при |
). |
|
|
Q 0 |
|
Вывод уравнения адиабаты. |
|
|
|
dU C dT и |
A = PdV : |
|
|
V |
|
|
|
CV dT РdV 0
Для 1 моля идеального газа:
РV RT T PV / R

|
dT PdV |
VdP Подставляя dT в уравнение: |
|||
|
|
R |
R |
|
|
|
R PdV VdP PdV 0 |
|
|||
|
СV |
|
|
|
Группируя PdV: |
|
СV R PdV CVVdP 0 |
||||
|
|
||||
|
CV R CP |
|
|
||
|
CP PdV CVVdP 0 |
Делим на СV PV |
|||
|
|
dV |
dP |
|
СP |
|
|
V |
P 0, |
где CV |
|
Т.к. γ = const ( для одноатомного газа γ = 5/3 ), то

|
|
dVV dPP |
0 lnV ln P const |
|||
|
|
ln PV const |
||||
|
|
|
|
|
|
|
|
|
PV |
|
const |
|
- |
|
|
|
|
уравнение Пуассона или |
||
|
|
|
|
|
|
уравнение адиабаты для |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
идеального газа |
Или в переменных Т и V уравнение адиабаты для идеального газа:
ТV 1 const