какая-то теория / деревья

ДИСКРЕТНАЯ МАТЕМАТИКА

ГРУППЫ 1/42, 1/147, 1/184

Ксенофонтова Ольга Леонидовна

ТЕОРИЯ ГРАФОВ

ДЕРЕВЬЯ

лекция

Деревья

Рассмотрим особый вид графов, называемый «деревом». Впервые ввел понятие деревьев физик Г. Кирхгофф в 1847 году. Будучи студентом Кёнигсбергского университета, он сформулировал законы, управляющие течением тока в электрических сетях.

Сети проводов могут быть рассмотрены как графы. Уравнения, которые вытекают из законов Кирхгоффа, не являются независимыми, и Кирхгофф использовал деревья для получения независимого подмножества уравнений. Независимо от Кирхгоффа А. Кэли, перечисляя изомеры насыщенных углеводородов, еще раз ввел понятие деревьев и первым исследовал их свойства. Как чисто математический объект деревья были введены и исследованы К. Жорданом.

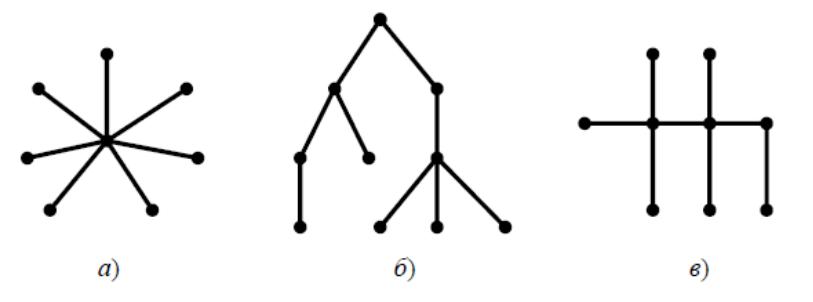
Примеры неориентированных деревьев

Неориентированные деревья

Неориентированным деревом называется связный неориентированный граф, не содержащий циклов. Можно сказать, что дерево является минимальным связным графом в том смысле, что при удалении хотя бы одного ребра он теряет связность.

Несвязный неориентированный граф без циклов, связные компоненты которого есть деревья, называется

лесом.

Любая часть леса или дерева также не имеет циклов, то есть является лесом или деревом.

Свойства деревьев

Теорема. Пусть граф G = (V, E) имеет n вершин и m ребер.

Тогда эквивалентными являются такие

утверждения:

1)G является деревом;

2)G является ациклическим графом и m = n −1;

3)G является связным графом и m = n −1;

4)любые две вершины графа G соединяет

единственная простая цепь;

5)G является ациклическим графом, но добавление любого нового ребра способствует

возникновению ровно одного цикла.

Деревья

Следствие. В любом дереве с числом вершин n ≥ 2 имеется не менее двух концевых вершин.

Следствие. Пусть G − лес с n вершинами и k компонентами, тогда G имеет n − k ребер.

Теорема (теорема Кэли). Число различных деревьев, которые можно построить на n вершинах, равно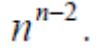

Остовное дерево

Остовным деревом или остовом

неориентированного графа G называется остовной подграф, содержащий все вершины графа G и являющийся деревом.

Остовным лесом неориентированного графа G называется остовной подграф, являющийся лесом.

В каждом графе существует остовное дерево. Его можно получить при помощи алгоритма поиска в ширину.

Остовное дерево

Остовное дерево

Построение последовательности деревьев при нахождении остовного дерева алгоритмом поиска в ширину равносильно удалению лишних ребер в каждом цикле исходного графа.

Число ребер, которые необходимо удалить в графе G для получения остовного дерева, называется

цикломатическим числом графа G и обозначается v(G) .