1.16.1. Моделирование вычислительного процесса систолического вычислителя

Моделирование вычислительного процесса систолического вычислителя для преобразования координат из одной системы координат в другую проведено на языке С. Окно программа имеет:

- 3 буфера памяти для элементов матрицы преобразования (матрица), исходных координат точки 3-х мерного пространства (вход) и преобразованных координат точки (выход);

- процессорное поле из 6-ти ПЭ, в которых отображаются результаты вычислений за последний такт;

- 2-е кнопки «Такт» - «Обнуление» и «Выход» , назначение которых состоит в последовательном переводе вычислительных тактов, обнулении измененных ячеек буферной памяти и ПЭ, выходе и завершении работы программы.

Программа может находиться в следующих состояниях:

- ввод данных в матрицу и вектор;

- вычислительный такт 1 – 14;

- обнуление;

- выход из программы.

Состояние ввода данных в матрицу и вектор позволяет задать положительные и отрицательные целочисленные значения для элементов матрицы и вектора. Поскольку матрица преобразования координат и вектор координат точки имеют фиксированную структуру, то нельзя изменять значения элементов матриц а₃₁, а₄₂, а₄₃, а₄₄ и элемент вектора в₁.

Состояния вычислительных тактов отображают стартовое, промежуточное и конечное состояние буферной памяти и процессорных элементов.

Состояние обнуления позволяет перевести программу из конечного в начальное состояние. При этом все ячейки буферной памяти обнуляются.

Состояние выхода из программы отображается после завершения вычислений и получения результата преобразования координат. При этом на кнопке «Такт» появляется надпись «Обнуление».

На следующих 4 рисунках приведены состояния программы в начале (такт 1), во время (такты 6, 9) и в конце вычислений (такт 14).

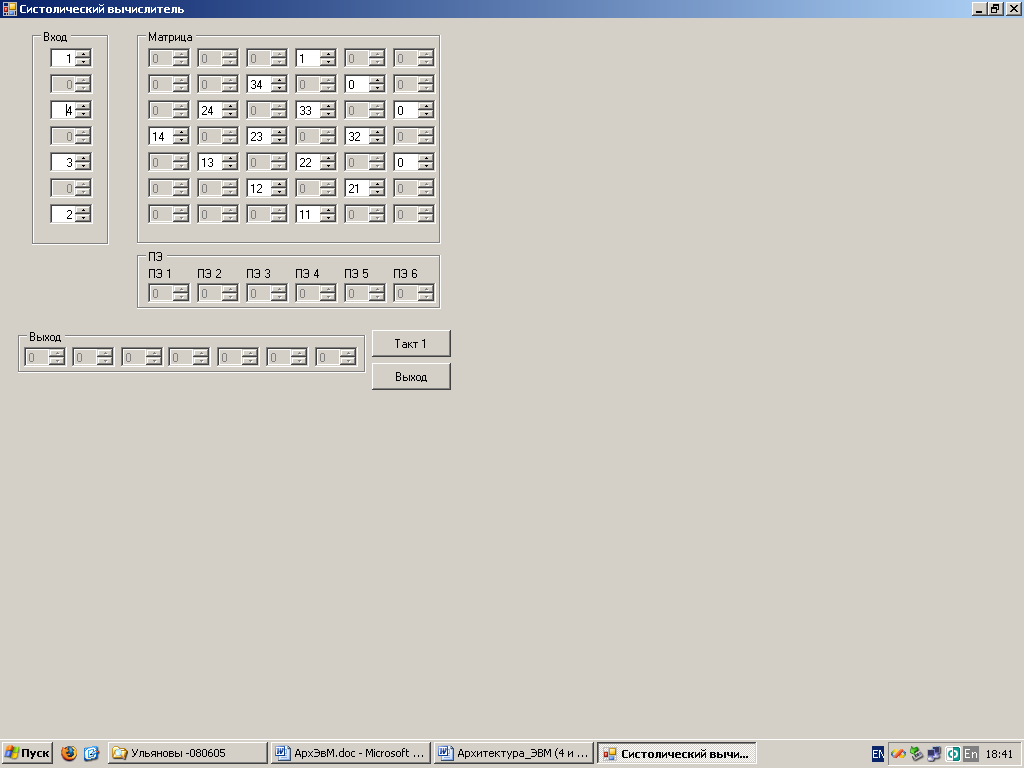
Рис. Ввод данных в матрицу и вектор Рис. Вычисления. Такт 6

Рис. Вычисления. Такт 9 Рис. Вычисления. Такт 14

Программа позволяет осуществить моделирование и визуализацию вычислительных и коммуникационных процессов в систолическом поле преобразования координат точки из одной системы координат в другую.

1.16.2. Разработка программы сравнительной оценки

Программа для сравнительной оценки ускорения, достигаемого в систолическом поле преобразования координат, создана в среде MATLAB2008. Сравнение производится с последовательным алгоритмом, выполняемым на одном ПЭ той же производительности. Графики достигаемого ускорения являются функцией от размерности матриц и соответственно от количества ПЭ в процессорном поле умножения матрицы на вектор. Матрица размерности (4Х4) и вектор размерности (4х1) соответствуют преобразованию координат в 3-х мерном пространстве. В общем случае матрица размерности (NХN) и вектор размерности (Nх1) соответствуют преобразованию координат в (N-1)- мерном пространстве.

Рис. Графики ускорения для систолического умножителя матрицы на вектор

(Этот график должен быть заменен на действительный!!!)

На рисунке показаны и совмещены графики ускорения для систолического умножителя матрицы на вектор в зависимости от размерности матриц и векторов и числа процессоров.

1.17. Постановка задачи по разработке параллельного алгоритма решения прямой задачи

Задана кинематическая схема манипулятора с шестью вращательными парами (рис.5). При этом число степеней свободы данного манипулятора равно шести. В некоторый момент времени известны значения обобщенных координат, поступающие с датчиков угловых относительных положений звеньев робота, определяющие положения всех звеньев манипулятора друг относительно друга.

Рис. 29 Кинематическая схема манипулятора с шестью вращательными парами

Требуется:

1. Определить положение и ориентацию последнего звена манипулятора (схвата).

2. Разработать последовательный алгоритм для прямой задачи.

3. Разработать параллельный алгоритм на основе последовательного для прямой задачи.

4. Выбрать структуру транспьютерных плат и распределить вычисления по

5. транспьютерам