
4879
.pdf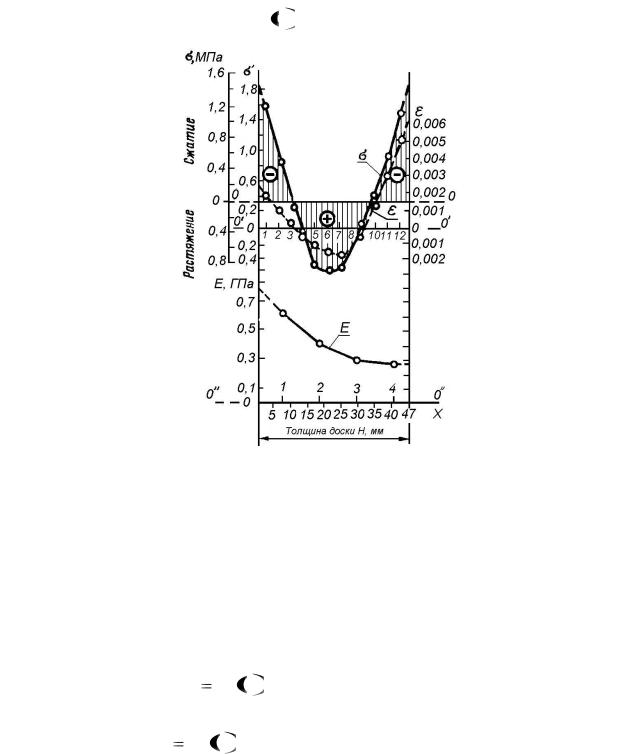
11
Масштаб принимают следующий: 1 см ординаты соответствует деформации, равной 0,001. Величины деформации со знаком плюс (+) откладывают вниз, а со знаком минус (–) – вверх от горизонтальной оси О'—О'. По полученным точкам строят кривую 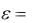 f1 x .
f1 x .
а
б
Рис. 3. Эпюра напряжений: а – кривые напряжений σ и деформаций ε; б – кривая модуля упругости Е
4.3.2. В нижней части графика (рис. 3, б) на участке горизонтальной оси О"—О", также равном величине Н в масштабе 2 : 1, откладывают значения высоты образцов секции 6, учитывая при этом ширину пропилов. На ординатах, проходящих через точки, соответствующие середине высоты каждого образца (рис. 3,б цифры 1; 2; 3; 4 на оси О" — О"), откладывают значения модуля упругости в масштабе: 1 см соответствует 1·108 Па (1·103 кгс/см2). По полученным
точкам строят кривую Е |
|
f2 |
x . |
4.3.3. По точке пересечения ординаты каждого слоя секции 5 с кривой |
|||
модуля упругости Е f |
2 |
x |
определяют значение Е для данного слоя. Полу- |
ченные значения Е для всех слоев секции 5 заносят в соответствующую графу табл. 2.
4.3.4. Напряжение (σ') в Па (кгс/см2) вычисляют по формуле
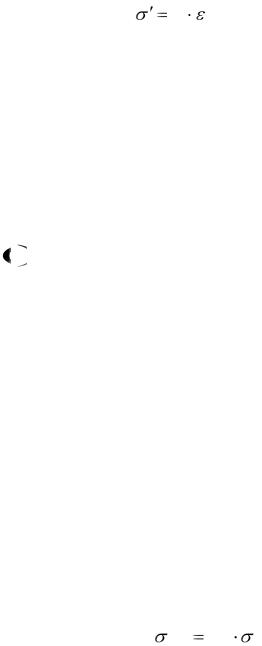
12 |
|
Е , МПа, |
(7) |
где Е – модуль упругости данного слоя, Па (кгс/см2); ε – деформация слоя.
Вычисление производят с погрешностью не более 5·103 Па (0,05 кгс/см2). Знак напряжений ζ' соответствует знаку деформации.
Полученные значения напряжений заносят в табл. 2.
4.3.5. Значения напряжений ζ' откладывают (рис. 3, а) на ординатах каждого слоя в зависимости от их знака вверх или вниз от оси О'—О' в масштабе: 1 см соответствует 2·105 Па (2 кгс/см2). По нанесенным на графике точкам строят кривую 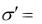 f3 x .
f3 x .
4.3.6. Исходя из условий равновесия напряжений, нулевую линию эпюры переносят из положения О'—О' в положение О—О с таким расчетом, чтобы площади эпюры с разными знаками были равны. Площади эпюры измеряют планиметрированием или другим способом с погрешностью не более 1 мм2. Соответственно новому положению нулевой линии переносят и шкалу напряжений. Окончательно величину напряжений а определяют по второй левой шкале (рис. 3, а). Для определения максимальных напряжений по ширине доски необходимо напряжения ζ увеличить в 1,3 раза.
4.4.7.Надпись к графику с эпюрой напряжений должна содержать марку пробы, название породы, влажность W1 в момент взятия пробы и влажность W2 после выдерживания.
4.4.8.Допустимая величина остаточных напряжений определяется по
формуле
доп |
0,7 |
, |
(8) |
|
|
|
где ζ – предел прочности на разрыв поперек волокон, МПа.
Выводы
По внешнему виду доски, по значению влажности пиломатериала, измеренному для секции 1, по перепаду влажности по толщине секции 2, а также по величине остаточных внутренних напряжений секции 4 определить категорию качества сушки исследуемого пиломатериала. По эпюре напряжений дать характеристику напряженного состояния древесины.
13
ПРАКТИЧЕСКАЯ РАБОТА № 2
НАГРЕВАНИЕ ДРЕВЕСИНЫ В РАЗЛИЧНЫХ СРЕДАХ
1. Цель работы
Определение температуры в заданных точках нагреваемого сортимента (пластины, цилиндра, куба) и построение расчетных температурных кривых в зависимости от времени нагревания, построения графиков распределения температурного поля по толщине прогреваемого сортимента.
2.Общие положения
Косновным технологическим целям тепловой обработки относятся: снижение твердости древесины (для улучшения качества еѐ механической обработки); повышение податливости древесины (для облегчения еѐ гнутья или прессования) и ускорение процессов склеивания древесины.
Способы тепловой обработки древесины различаются по используемым для этой цели видам теплообмена и по применяемым агентам обработки. Средой для нагревания древесных сортиментов могут служить воздух или его смесь с топочными газами, насыщенный водяной пар, вода. Насыщенный пар и вода имеют при тепловой обработке древесины преимущественное применение. Их использование характеризуется весьма интенсивным поверхностным теплообменом.
Основная задача расчета процессов нагревания древесных сортиментов – установить продолжительность доведения их до заданной температуры или, наоборот, установить температуру материала после обработки в течение заданного времени.
Процессы теплообмена сложны и определяются состоянием среды и характером нагреваемого материала (порода, влажность, температура, направление теплового потока и др.).
Условия нагревания древесины по температурным режимам, размерам и свойствам материала разнообразны. Для унификации решения подобных задач разработаны и применяются обобщенные теплофизические комплексы, называемые критериями теплового подобия.
14
3.Содержание работы
3.1.Теоретическое определение температуры пиломатериалов в заданных точках при нагревании их в горячей воде, воздухом и паром графоаналитическим методом.
3.3.Построение теоретических (расчетных) температурных кривых для заданных точек нагреваемого сортимента в зависимости от времени нагревания
ипостроение графиков (опытных и расчетных) распределения температурного поля по толщине нагреваемого сортимента.
3.4.Сравнение температурных кривых и определение наибольшего отклонения между расчетными данными при нагревании в горячей воде, воздухом и паром.
3.5.Выводы по результатам работы.
4.Исходные данные
Исходные данные для выполнения расчетов:
-порода;
-размеры пиломатериалов (толщина × ширина × длина), размеры круглых лесоматериалов (диаметр, длина);
-начальная влажность W, %;
-продолжительность нагрева, ч;
-координаты расчетных точек;
-температура нагревающей среды, °С;
-начальная температура древесины, °С.
Исходные данные для выполнения расчетов принимают по заданию преподавателя.
5. Определение температуры древесины графоаналитическим методом при нагревании в воде
Нагревание древесины представляет собой типичный нестационарный процесс, при котором температурное поле изменяется во времени.
Задачи расчета процесса нагревания тела сводятся обычно к одной из
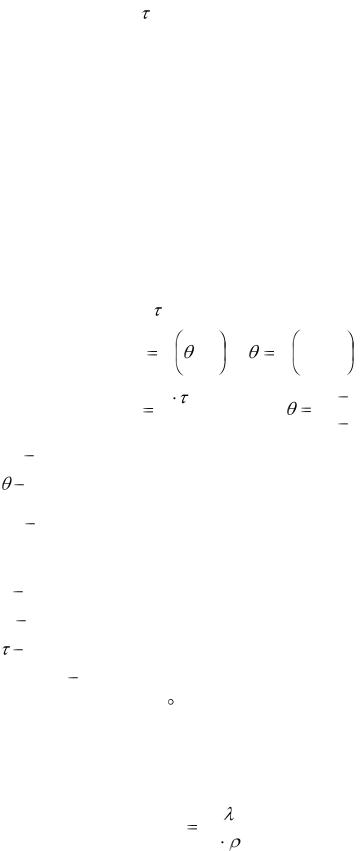
15
двух задач:
- определение температуры t, которую будет иметь тело в заданной точке по прошествии времени ;
- определение времени, необходимого для нагревания тела в точке до заданной температуры.
Связи между искомыми переменными заложены в дифференциальном уравнении теплопроводности.
На практике расчеты нагревания материалов, в том числе и древесины, проводятся графическими методами, основанными на связях между безразмерными величинами (критериями, числами), характерными для данного процесса, вытекающими из решений уравнений теплопроводности.
В условиях интенсивного теплообмена, характерного для нагревания в воде и насыщенном паре, когда (tn = tc) задача по определению температуры по заданному времени tx = f ( ; x) преобразуется в задачу
|
F |
f |
; |
x |
и |
f F ; |
x |
|
|
||
|
|
|
|
|
|
||||||
|
o |
|
|
R |
|
o |
R |
|
|
||
|
F |
a |
, |
|
(9) |
|
tc |
|
t x |
, |
(10) |
|
|
|
|
|
|
|
|||||
|
o |
R2 |
|
|
|
|
tc |
|
to |
|
|
|
|
|
|
|
|
|
|
|
|||
где |
F0 критерий Фурье; |
|
|
|
|
|
|
|
|
|
|
|
безразмерная температура; |
|
|
|
|
|
|
||||
x |
безразмерная координата точки, в которой определяется темпе- |
|
|
||
R |
||
|
||
|
ратура; |
храсстояние точки от поверхности сортимента, м;
R радиус цилиндра или половина толщины пластины, м;
продолжительность нагревания, с;
tо; tc; tx соответственно температура среды, начальная и искомая температура тела, С.
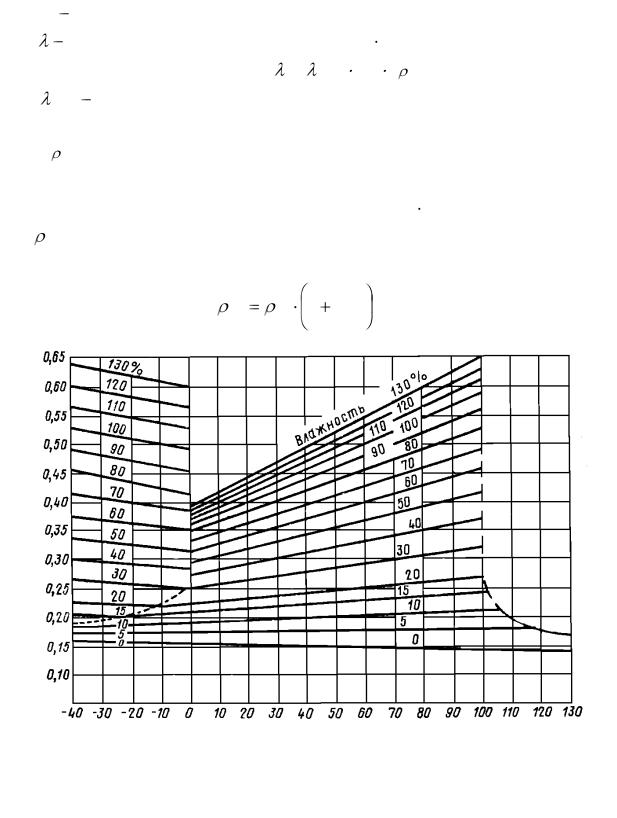
Для практического решения задачи необходимо располагать данными о теплофизических характеристиках материала, которые связаны между собой
соотношением |
|
|
|
|
а |
|
|
, м2/с, |
(11) |
С |
|
|||
|
w |
|
||
|
|
|
||
16
где |
а коэффициент температуропроводности, м2с; |
|
|||||||
|
коэффициент теплопроводности, Вт/м град, который равен |
|
|||||||
|
|
|
= ном Кх К , |
|
(12) |
||||
где |
ном определяется в зависимости от влажности и температуры мате- |
||||||||
|
риала, (рис. 4); |
|
|
|
|
|
|
|
|
|
К ; Кх – соответственно поправки на плотность, направление теплового |
||||||||
|
потока; |
|
|
|
|
|
|
|
|
|
С – удельная теплоемкость древесины, кДж/(кг град), (рис. 5);. |
|
|||||||
|
w – плотность древесины при определенной влажности, кг/м3, (рис. 6); |
||||||||
при начальной влажности Wн >30 %, также можно пользоваться формулой |
|
||||||||
|
|
|
|
Wн |
3 |
|
|
||
|
w |
б |
1 |
|
|
|
, кг/м |
. |
(13) |
|
100 |
||||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
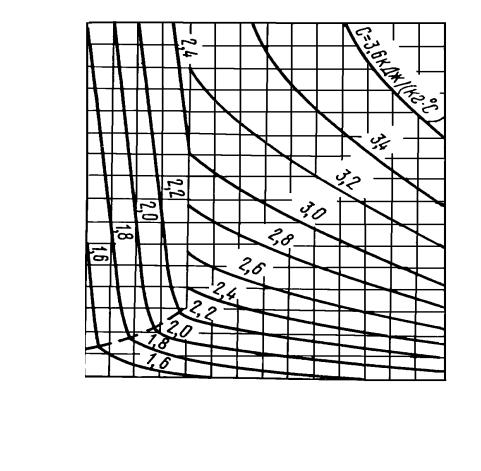
Коэффициент теплопроводности λ, Вт/(м∙ºС)
Температура t, ºC
Рис. 4 Диаграмма номинального (ρб = 500 кг/м3) коэффициента теплопроводности древесины поперек волокон при атмосферном давлении
Значение коэффициента Кρ в зависимости от базисной плотности древесины
ρб , кг/м3 |
350 |
400 |
450 |
500 |
550 |
600 |
650 |
|
|
|
|
|
|
|
|
Кρ |
0,81 |
0,87 |
0,93 |
1,0 |
1,11 |
1,26 |
1,45 |
|
|
|
|
|
|
|
|
17
Значение коэффициента Кх, учитывающего направление теплового потока
Группы пород |
Коэффициент Кх при направлении теплового потока |
||
|
|
|
|
|
радиальном |
тангенциальном |
вдоль волокон |
|
|
|
|
Хвойные |
1,0 |
1,0 |
2,2 |
|
|
|
|
Лиственные с неразвитыми серд- |
|
|
|
цевинными лучами (береза, осина, |
1,0 |
1,0 |
2,0 |
липа и др.) |
|
|
|
|
|
|
|
Лиственные с развитыми сердце- |
|
|
|
винными лучами (дуб, бук, клен и |
1,0 |
0,87 |
1,6 |
др.) |
|
|
|
|
|
|
|
Все теплофизические характеристики определяются на графиках с учетом породы, влажности, температуры древесины и направления теплового потока.
|
160 |
|
150 |
|
140 |
|
130 |
|
120 |
|
110 |
, % |
100 |
90 |
|
Влажность |
80 |
70 |
|
60 |
|
|
50 |
|
40 |
|
30 |
|
|
|
20 |
|
10 |
|
0 |
-40 -20 |
0 |
20 |
40 |
60 |
80 |
100 |
|
|
Температура, ºС |
|
|
|
|
Рис. 5 Диаграмма удельной теплоѐмкости древесины
Прямоугольные сортименты (доски, брусья) можно принимать за неограниченные пластины, если отношение их толщины S1 к ширине S2 меньше 0,3.
|
|
18 |
|
При |
S1 |
0,3 доску или брус следует рассматривать как параллелепипед неог- |
|
S2 |
|||
|
|
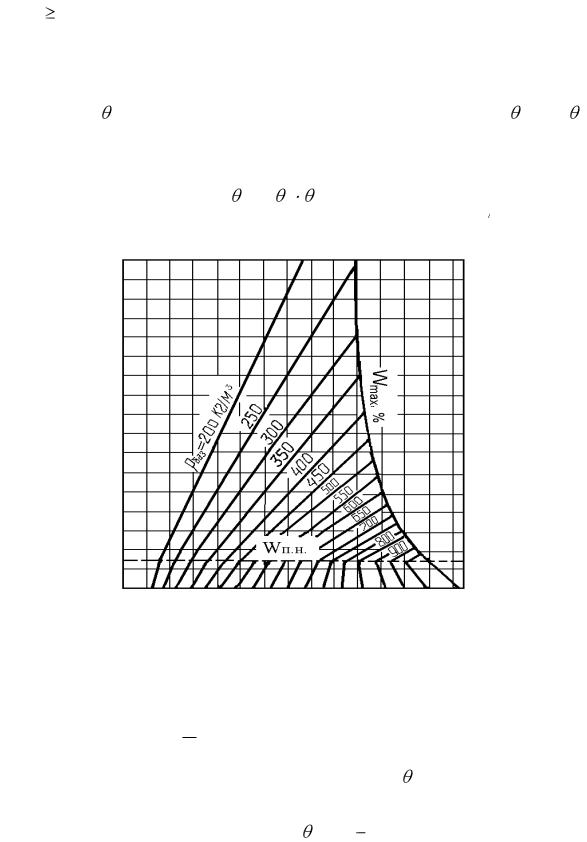
раниченной длины, образованный пересечением двух пластин толщиной S1 и S2. Безразмерная температура в определенной точке этого прямоугольного параллелепипеда пр равна произведению безразмерных температур 1, θ3 и 2, которые получились бы в этой точке при раздельном нагревании пластин и S1, S2 и S3
Влажность, %
пр = 1 |
2 ·θ3. |
(14) |
300
260
220
180
140
100
60
20
200 400 600 800 1000
Плотность, кг/м3
Рис. 6. Плотность древесины
В задаче по определению температуры tx последовательность расчетов
следующая: по заданной x и подсчитанному значению F0 по номограмме (рис.
R
7) определяют значение безразмерной температуры . Фактическая температура tх определяется из выражения
tх = tс  пр·(tс t0). (15)
пр·(tс t0). (15)
По данным табл. 4 построить графики изменения температуры нагрева бруска в заданных точках в зависимости от продолжительности нагревания в
|
19 |
координатах: |
(время в мин. на оси абсцисс), t температура ( С) на оси ор- |
динат рис. 8 и графики распределения температурного поля по толщине нагреваемого бруска на каждый этап продолжительности нагревания бруска рис. 9.
|
|
а |
|
|
|
|
б |
|
|
|
|
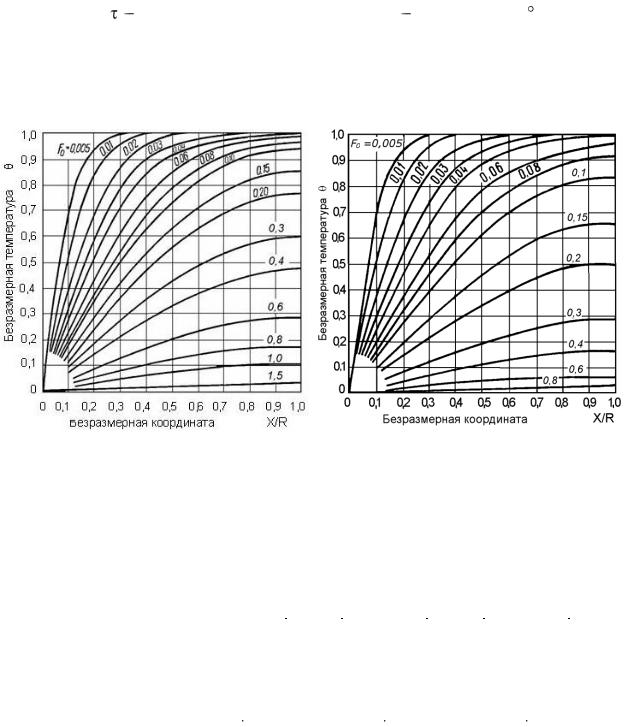
Рис. 7. Номограмма для определения безразмерной температуры: |
|
|
|||||||
|
а – неограниченной пластины; б – неограниченного цилиндра |
|
|
|||||||
|
|
|
|
|
|
|
|
Таблица 4 |
||
|
|
Расчет продолжительности нагревания древесины |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Вре- |
Крите- |
Крите- |
Точка 1 |
Точка 2 |
|
Точка 3 |
|
|||
мя |
рий |
рий |
|
|
|
|
|
|
|
|
Общая без- |
Иско- |
Общая без- |
Иско- |
|
Общая без- |
Иско- |
|
|||
нагре |
Фурье, |
Фурье, |
размерная |
мая |
размерная |
мая |
|
размерная |
мая |
|
вания |
Fo1 |
Fo2 |
температу- |
темпе- |
температу- |
темпе- |
температу- |
темпе- |
|
|
τ, с |
(S1) |
(S2) |
ра |
ратура, |
ра |
ратура, |
|
ра |
ратура, |
|
|
|
|
θ=θ1 θ2·θ3 |
t, ºC |
θ=θ1 θ2·θ3 |
t, ºC |
|
θ=θ1 θ2·θ3 |
t, ºC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20
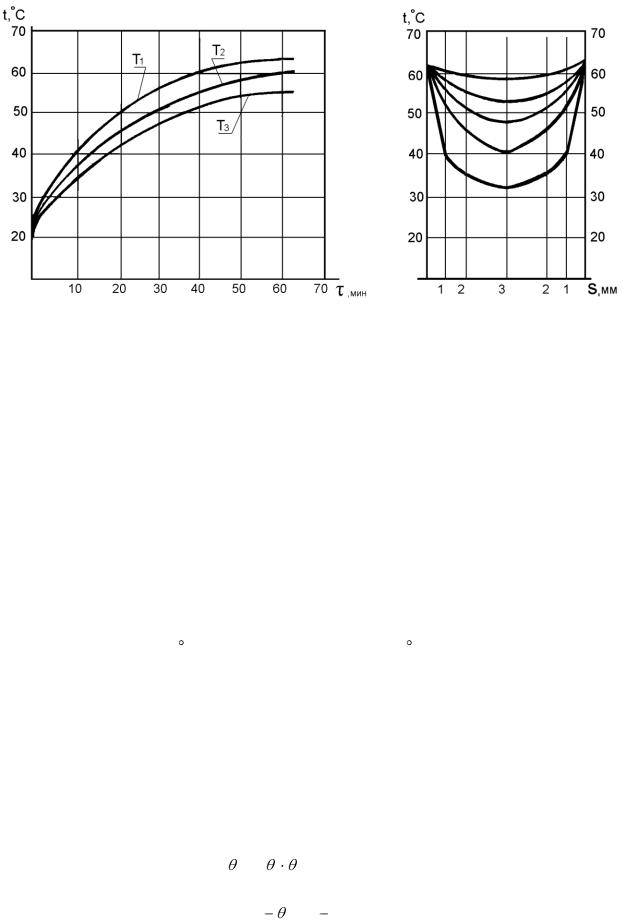
Рис. 8. График изменения температуры |
Рис. 9. Распределение температурного поля |
нагрева бруска в заданных точках 1, 2, 3 в |
по толщине нагреваемого бруса на каждый |
зависимости от продолжительности нагре- |
этап продолжительности нагревания бруса |
вания |
|
6. Пример расчета нагревания древесины графоаналитическим методом
Используя исходные данные (порода, базисная плотность, размеры образца, температура воды, начальная температура и влажность древесины, безразмерные координаты заданных точек), рассчитать температуру в заданных точках. Расчет продолжительности нагревания древесины выполнить в форме табл. 4.
Пример: сосновый брусок размером S1 = 50 мм, S2 = 100 мм, влажностью 50 %, начальной температурой 18 C нагревается в воде при tс = 80 С в течение 50 мин.
Определить изменение температуры нагревания через каждые 10 мин в точках 1,
2, 3, безразмерные координаты которых относительно размера S1 составляют |
|
x |
= 0,25; |
x |
= |
|||||
|
|
|
||||||||
|
|
|
|
|
|
|
R |
R |
||
0,5; |
x |
= 1. Безразмерная координата относительно размера S2 составляет |
x |
= 1. |
|
|
||||
|
|
|
|
|
||||||
|
R |
|
R |
|
|
|
|
|
||
|
|
Задача решается путем последовательного определения безразмерной температуры в |
||||||||
точках неограниченных пластин толщиной S1, S2 и S3, определения общего значения безраз- |
||||||||||
мерной температуры относительно толщины S1, S2 и S3 |
|
|
|
|
|
|
|
|||
|
|
пр = 1 |
2 ·θ3 |
|
|
|
|
|
|
|
и определения искомой температуры по формуле |
|
|
|
|
|
|
|
|||
|
|
t = tс |
пр (tс t0). |
|
|
|
|
|
|
|
