
4689
.pdf
11
Так как
t1
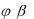
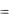 F t, x t , x
F t, x t , x t dt,
t dt,
t0
то, используя правило дифференцирования интеграла по параметру и формулу для производной сложной функции, имеем
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fx |
|
x t |
Fx |
|
|
x |
t |
dt. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку |
|
x |
t |
|
x t |
x t |
x t |
и |
|
|
x |
t |
|
x |
t |
x t |
x t , то |
||
|
|
|
|
|
|||||||||||||||
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fx t, x t , x t x t |
Fx t, x t , x t x t dt. |
|
|
||||||||||||
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда получаем |
0 |
|
Fx |
t, x t , x t |
x t |
Fx |
t, x t , x t |
x t |
dt. |
|
|
||||||||
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По определению VI 0 является вариацией функционала. В силу теоремы 1.1' необходимое условие экстремума функционала заключается в обращении в нуль его вариации: 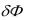 0 . Для функционала (1.1) это условие имеет вид
0 . Для функционала (1.1) это условие имеет вид
|
t1 |
|
|
|
|
|
|
Fx x |
Fx |
x dt |
0 . |
||
|
t0 |
|
|
|
|
|
|
Проинтегрируем второе слагаемое по частям, принимая во внимание, что |
|||||
x t |
x t . Получим |
|
|
|
|
|
|
|
t1 |
t1 |
|
d |
F xdt . |
|
|
|
||||
|
F x |
F |
|
|||
|
|
x |
|
|||
|
x |
|
|
dx |
x |
|
|
|
t0 |
t0 |
|
|
|
Ho |
|
|
|
|
|
|
|
x t0 x t0 x t0 |
0 и x t1 |
x t1 x t1 0 , |
|||
потому что все допустимые кривые в рассматриваемой задаче проходят через фиксированные граничные точки. Следовательно,
|
|
t1 |
|
|
d |
|
|
|
|
|
|
|
|
F |
|
|
F |
|
xdt. |
|
|
||
|
|
|
|
|
|
x |
|
|
|||
|
|
x |
|
|
dt |
|
|
|
|
||
|
|
t0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Итак, необходимое условие экстремума приобретает вид |
|
||||||||||
|
|
t1 |
|
d |
|
|
|
|
|
|
|
|
|
F |
|
F |
|
xdt |
0, |
(1.3) |
|||
|
|
|
|
|
|||||||
|
|
x |
|
dt |
x |
|
|
|
|
||
|
|
t0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
причем первый множитель F |
d |
F на кривой x |
x t , реализующей экстремум, |
||||||||
|
|||||||||||
x |
dt |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
является заданной непрерывной функцией, а второй множитель |
x , ввиду про- |
||||||||||
извола в выборе кривой сравнения x t |
, является произвольной функцией, удов- |
||||||||||
летворяющей лишь некоторым весьма общим условиям, а именно: функция x в граничных точках t t0 и t t1 обращается в нуль, непрерывна и дифференци-

12
руема один или несколько раз, x или x и x малы по абсолютной величине. Для упрощения полученного условия (1.3) воспользуемся следующей леммой.
малы по абсолютной величине. Для упрощения полученного условия (1.3) воспользуемся следующей леммой.
Основная лемма вариационного исчисления. Если для каждой непре-
рывной функции |
t |
|
|
t1 |
|
|
g t t dt 0, |
|
|
t0 |
|
где функция g t |
непрерывна на отрезке |
t0 , t1 , то |
|
g t |
0 |
на этом отрезке.
Доказательство см. в [2], стр.23.
Замечание. Утверждение леммы и ее доказательство не изменятся, если
на функцию t наложить дополнительные ограничения: |
t0 |
t1 |
0 , t |
||
|
|
|
|
|
|
имеет непрерывные производные до порядка p , |
s t |
s |
0,1,..., q; |
q |
p . |
Применим основную лемму для упрощения полученного выше необходимого условия (1.3) экстремума функционала (1.1). Все условия леммы вы-
полнены, следовательно, F |
d |
F |
0 на кривой x |
x t , реализующей экстре- |
||
|
||||||
x |
dt |
x |
|
|
|
|
|
|
|
|
|
|
|
мум рассматриваемого функционала (1.1), т. е. x |
x t является решением диф- |
|||||
ференциального уравнения второго порядка |
|
|||||
|
|
F |
|
d |
F 0 , |
|
|
|
|
|
|
||
|
|
x |
|
dt |
x |
|
|
|
|
|
|
|
|
или в развернутом виде |
|
|
|
|
|
|
Fx |
|
Ftx |
Fxx x Fx x x 0 . |
|
||
Это уравнение носит имя Эйлера, впервые опубликовавшего его в 1744 году. Определение. Решения уравнения Эйлера x x t, c1 , c2  называются экс-
называются экс-
тремалями. Экстремаль, удовлетворяющая заданным краевым условиям, назы-
вается допустимой экстремалью.
Итак, доказана
Теорема 1.2 (необходимое условие экстремума функционала). Экстре-
мум функционала (1.1) при условиях (1.2) может достигаться только на допустимых экстремалях.
Для нахождения кривой, реализующей экстремум функционала (1.1), интегрируем уравнение Эйлера и определяем обе произвольные постоянные, входящие в общее решение этого уравнения, из условий (1.2). Только на удовлетворяющих этим условиям экстремалях может реализоваться экстремум функционала. Однако для того чтобы установить, реализуется ли на них в действительности экстремум, и притом максимум или минимум, надо воспользоваться достаточными условиями экстремума, изложенными в [2], глава III.
Иногда существование решения вариационной задачи очевидно из физического или геометрического смысла задачи. Если решение уравнения Эйлера,

13
удовлетворяющее краевым условиям, единственно, то эта единственная допустимая экстремаль и будет решением рассматриваемой задачи.
1.2. Практическая часть
Задача 1. Найти экстремум функционала
t1
x
t0
F t, x t , x t
t  dt
dt
на непрерывно дифференцируемых на t0 , t1  кривых, закрепленных на концах:
кривых, закрепленных на концах:
x t0 |
x0 , x t1 |
x1 . |
Алгоритм решения задачи 1
1.Выписать подынтегральную функцию F t, x t , x t
t .
.
2.Найти Fx , Fx и dtd Fx
и dtd Fx .
.
3. Записать уравнение Эйлера: F |
d |
F 0 |
|
||
x |
dt |
x |
|
|
4.Найти экстремали - решения уравнения Эйлера.
5.Найти допустимые экстремали, удовлетворяющие заданным краевым усло-
виям: x t0  x0 , x t1
x0 , x t1  x1 .
x1 .
6. Доказать, если возможно, что функционал на допустимой экстремали достигает экстремума.
Примеры оформления отчета по практическому занятию
Пример 1.1. Найти экстремум функционала
|
|
|
|
|
0 |
|
|
|
|
x |
et x 2 6x 2 dt |
|
|
|
|
|
1 |
при условиях x( |
1) |
0 , |
x 0 |
1. |
|
Решение. |
|
|
|
|
|
1. Здесь F t, x t , x |
t |
et |
x 2 |
6x 2 .. |
|

14
2. Найдем |
F |
, |
F |
|
и |
d |
|
F |
. Имеем F et |
x |
2 |
6x 2 |
et 0 |
12x |
12et x ; |
|||||||
x |
|
|
||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
dt |
x |
|
|
x |
|
|
x |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
F |
|
et x 2 |
6x 2 |
x |
et |
2x 0 2et x |
; |
|
|
|
|
|
|
||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
d |
F |
|
d |
2et x |
|
|
2et x 2et x |
2et x x . |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
dt |
x |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. |
|
Уравнение |
|
Эйлера |
имеет |
вид: |
12et x |
2et x |
x |
0 . |
Отсюда имеем |
|||||||||||
2et |
x |
x |
6x |
|
0 . Так как et |
0 , то получаем равенство: |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
6x |
0 . |
|
|
|
|
4. Последнее уравнение является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Его характери-
стическое уравнение k 2 k 6 0 имеет корни k |
3 и k |
2 |
2 , поэтому общее |
||
|
|
1 |
|
|
|
решение уравнения Эйлера имеет вид |
|
|
|
|
|
x(t) c e 3t |
c |
e2t . |
|
|
|
1 |
2 |
|
|
|
|
Итак, найдены экстремали задачи.
5. Найдем допустимые экстремали, подобрав c1 , c2 так, чтобы выполнялись краевые условия: x( 1) 0 , x 0 1. Учитывая эти условия и вид экстремалей, получаем линейную систему для определения постоянных c1 , c2 :
1. Учитывая эти условия и вид экстремалей, получаем линейную систему для определения постоянных c1 , c2 :
|
|
|
|
|
|
|
|
|
c e3 |
|
c |
e 2 |
0, |
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
c1 |
|
c2 |
1. |
|
|
||||
Откуда находим: c1 |
|
|
1 |
|
и |
c2 |
|
e |
5 |
|
. |
Поэтому допустимая экстремаль x t |
||||||||
|
1 |
e5 |
|
|
|
|
1 e5 |
|
|
|
|
|
|
|
ˆ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xˆ |
t |
1 |
|
e 3t |
|
e5 |
|
e2t |
|
e 3t |
e2t 5 |
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
e5 |
|
|
|
|
|
|
|
e5 |
||||||||
|
|
|
|
1 |
|
1 e5 |
|
|
1 |
|
||||||||||
6. Докажем, что допустимая экстремаль доставляет экстремум данному функционалу. Для любой непрерывно дифференцируемой на отрезке 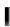 1;0
1;0 функции x t , удовлетворяющей заданным краевым условиям, имеем
функции x t , удовлетворяющей заданным краевым условиям, имеем
15
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2 |
6 xˆ x 2 |
|
xˆ 2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
xˆ x |
|
xˆ |
et |
xˆ x |
|
|
|
|
6xˆ 2 dt |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
xˆ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
et |
|
|
2xˆ x |
|
x 2 |
|
6xˆ 2 |
12xˆx 6x 2 |
|
xˆ 2 |
|
|
6xˆ 2 dt |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
et 2ˆx x |
|
x 2 |
12ˆxx 6x2 |
|
2et ˆx x dt |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
dt |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 et |
|
x 2 |
|
6x 2 dt |
0 |
d |
|
2et xˆ x dt |
|
0 |
12et xˆ |
|
d |
|
2et xˆ xdt. |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 dt |
|
|
|
|
dt |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
d |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2e5 |
3 |
|
|
|||
Так как |
x( |
1) |
0 , x 0 |
|
1, то |
|
2e x x dt 2e |
x x |
|
1 |
|
2x 0 |
|
|
0 |
. Поскольку |
||||||||||||||||||||||||||
|
|
dt |
|
|
|
|
|
e5 |
|
1 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
t ˆ |
|
|
|
t ˆ |
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
d |
|
|
|
|
|
|
|||
x t |
является решением уравнения Эйлера, |
то |
|
|
12e x |
|
2e |
x |
|
xdt |
0 . Очевид- |
|||||||||||||||||||||||||||||||
|
|
dt |
|
|
||||||||||||||||||||||||||||||||||||||
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
t ˆ |
|
|
|
|
t ˆ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
но, |
что |
e |
t |
|
x |
2 |
|
6x |
2 |
dt |
|
0 . Итак, |
|
|
ˆ |
|
|
|
ˆ |
|
0 . |
Следовательно, на допусти- |
||||||||||||||||||||
|
|
|
|
|
|
|
x x |
|
|
|
x |
|
||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
достигается абсолютный минимум. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
мой экстремали x t |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: минимум функционала |
|
x |
et |
x 2 |
|
|
6x 2 |
dt достигается на кривой |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x t |
|
e 3t |
e2t 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
1 |
e5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Пример 1.2. На каких кривых может достигать экстремума функционал |
|||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x 2 |
|
|
x 2 |
|
dt при условиях x(0) |
0 , |
x |
|
|
|
|
1 ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1. F t, x t , x t |
|
|
|
x 2 |
|
x2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. Найдем F |
|
, |
F |
|
и |
d |
F |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
dt |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
F |
|
x |
|
2 |
|
x2 |
2x ; |
F |
|
x |
2 |
|
x2 |
|
|
|
|
2x ; |
d |
F |
|
2x . |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ч |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
ч |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
x |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. Уравнение Эйлера имеет вид: |
2x |
|
2x |
0 . Отсюда имеем x |
|
x |
0 . |
|||||||||||||||||||||||||||||||||||
4. Для последнего уравнения запишем характеристическое уравнение: k 2 1 0 . Его корни: k1 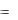 i и k 2 i . Значит, экстремали имеют вид: x t
i и k 2 i . Значит, экстремали имеют вид: x t c1 cost c2 sint .
c1 cost c2 sint .

16
5. Найдем |
допустимые |
экстремали, |
используя |
краевые условия: x(0) 0 и |
|||||||||||||||
x |
|
|
1. Учитывая вид функции x t |
, получаем c1 0 и c2 |
1 . Значит, единст- |
||||||||||||||
|
|||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
венная допустимая экстремаль x t |
sint . |
|
|
|
|
|
|
||||||||||||
Ответ: экстремум может достигаться лишь на кривой x t |
sint . |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Пример 1.3. Найти экстремум функционала |
x |
x 2 |
2txx |
dt при усло- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
виях |
x 1 |
0 , x 0 |
1. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. F t, x t , x |
t |
|
x2 |
2txx ; |
|
|
|
|
|
|
|
|
|
||||||
2. Найдем |
F |
, F |
|
и |
d |
F |
: |
|
|
|
|
|
|
|
|
||||
x |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x |
|
|
dt |
x |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
F |
|
x2 |
|
2txx |
|
2x 2tx ; |
F |
x2 2txx |
|
2tx ; |
d |
F |
2x |
2tx . |
||
|
|
|
|
|
x |
x |
|
||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
dt |
x |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Уравнение Эйлера имеет вид: превращается в тождество.
2x 2tx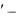 2x 2tx
2x 2tx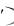 0 , т. е. уравнение Эйлера
0 , т. е. уравнение Эйлера
4 - 5. Любая непрерывно дифференцируемая на отрезке  1;0
1;0 функция, удовлетворяющая заданным краевым условиям, является допустимой экстремалью.
функция, удовлетворяющая заданным краевым условиям, является допустимой экстремалью.
|
d |
|
|
0 |
d |
|
0 |
|
|
|
|
|
|
||||
6. Поскольку x2 2txx |
tx2 |
, то x |
|
tx2 (t) dt tx2 (t) |
0 1 x 2 1 0 , так |
|||
dt |
1 dt |
|||||||
|
|
|
|
1 |
||||
как x 1
1 0 .
0 .
Ответ: функционал равен нулю для всех непрерывно дифференцируемых на отрезке  1;0
1;0 функций, удовлетворяющих заданным краевым условиям.
функций, удовлетворяющих заданным краевым условиям.
1.3. Задачи для самостоятельного решения
|
Найдите допустимые экстремали для указанных функционалов при за- |
данных условиях: |
|
|
2 |
1. x |
(x 2 2xx x 2 )dt; x(1) 1; x(2) 0; |
|
1 |
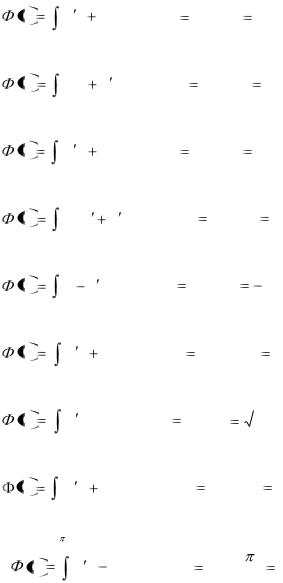
17
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
x |
(x 2 |
tx)dt; |
x(0) |
|
0; |
x(1) |
0; |
|
|||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
x |
(t 2 x |
x 2 )dt; |
|
x(0) |
0; |
x(1) |
0; |
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
x |
(x 2 |
tx)dt; |
x(0) |
|
0; |
x(1) |
0; |
|
|||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
x |
(12tx |
x 2 )dt; |
x(0) |
3; |
x(1) |
0; |
|||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
x |
(x x 2 )dt; |
x(0) |
0; |
x(1) |
1; |
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
x |
|
(x 3 |
2x)dt; |
x(0) |
|
0; x(1,5) |
1; |
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
x |
|
(x 2 x 2 )dt; x(0) |
|
|
|
|
|
|
|||||||
|
1; x(1) |
2; |
|
|||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. |
x |
( x 2 |
6xt 2 )dt; |
x(0) |
|
4; |
x(2) |
6; |
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. |
x |
|
|
(x 2 |
x 2 )dt; |
x(0) |
|
0; |
x( |
|
|
) |
|
1 . |
||
|
|
|
|
|
|
|||||||||||
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1.4.Вопросы для самоконтроля и повторения
1.Приведите постановку задачи вариационного исчисления.
2. Сформулируйте определение близости кривых нулевого (первого, k-го) порядка.
3.Дайте определение линейного функционала.
4.Приведите определение вариации функционала.
5. Чем отличается сильный минимум функционала от слабого?
6.Сформулируйте и докажите необходимое условие экстремума функционала.
7.Сформулируйте основную лемму вариационного исчисления.

18
8.Приведите вывод уравнения Эйлера. Как используется это уравнение?
9.Дайте определения экстремали и допустимой экстремали.
2. Оптимальное управление
Цель: Познакомить с принципом максимума Понтрягина на примере задачи об оптимальном быстродействии. Научить использовать этот принцип при решении задач.
2.1. Теоретическая часть
Сформулируем задачу оптимального управления. Будем рассматривать поведение объекта, состояние которого в каждый момент времени характеризуется вектором x(t) Rn . Предполагается, что движением объекта можно управлять при помощи кусочно – непрерывных управляющих функций u(t) , значения которых принадлежат некоторому множеству 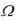 Rm . Закон управления объекта записывается в виде
Rm . Закон управления объекта записывается в виде
|
|
|
dx |
f (x,u), |
|
(2.1) |
|
|
|
|
|
|
|||
|
|
|
dt |
|
|||
|
|
|
|
|
|
|
|
где функции f i (x1 ,..., xn , u) и |
|
f i (x1 ,..., xn ,u) |
, |
i, j 1,2,..., n, определены и непрерыв- |
|||
|
|
||||||
|
|
|
|
x j |
|
|
|
ны на прямом произведении R n |
. |
|
|
|
|||
Допустим, существует управление u |
u(t) , которое переводит состояние |
||||||
x0 в состояние x1 . То есть, существуют два момента времени t0 |
t1 такие, что |
||||||
решение уравнения (2.1) удовлетворяет условиям x(t0 ) x0 , x(t1 ) |
x1 (фиксиро- |
||||||
ваны только x0 и x1 , но не t0 , |
t1 ). Задача состоит в том, чтобы выбрать наиболее |
||||||
выгодное управление u t со значениями в |
, переводящее точку x0 в точку x1 . |
||||||
Выгодность управления u(t) оценивается функционалом J u . Управление считается оптимальным, если функционал J u принимает минимальное значение. Часто функционал J u
принимает минимальное значение. Часто функционал J u задается в виде интеграла
задается в виде интеграла
t1
J u 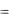 f 0 (x(t), u(t))dt,
f 0 (x(t), u(t))dt,
t0
где f 0 (x, u) - заданная функция нескольких переменных.

19
Связь с вариационным исчислением. Рассматривавшуюся ранее задачу отыскания экстремума функционала (1.1) можно записать в виде задачи опти-
мального управления, если положить |
dx t |
u(t) и |
; . |
||||
|
dt |
||||||
|
|
|
|
|
|
||
Если |
f 0 (x(t), u(t)) 1, то |
J u t |
t |
0 |
, и мы получаем задачу об оптимальном |
||
|
|
1 |
|
|
|
|
|
быстродействии. А именно, требуется найти оптимальное управление со значениями в , которое переводит систему из состояния x0 в состояние x1 за кратчайшее время.
Эффективным методом решения задач оптимального управления является использование необходимого условия оптимальности управления - принципа максимума Понтрягина. Сформулируем этот знаменитый принцип для задачи об оптимальном быстродействии. Для этого введем вспомогательную векторфункцию ψ t и с еѐ помощью составим функцию
и с еѐ помощью составим функцию
|
n |
H (x, ψ,u) ψ,f (x,u) |
i f i (x, u), |
|
i 1 |
где  .,.
.,. означает скалярное произведение. Вектор-функция ψ(t) называется сопряженной переменной, а функция H - функцией Понтрягина или гамильтонианом. Предполагается, что координаты i (t) вектор-функции ψ(t) являются решением системы дифференциальных уравнений
означает скалярное произведение. Вектор-функция ψ(t) называется сопряженной переменной, а функция H - функцией Понтрягина или гамильтонианом. Предполагается, что координаты i (t) вектор-функции ψ(t) являются решением системы дифференциальных уравнений
d |
i |
|
H |
|
|
|
|
, i 1,2,..., n . |
(2.2) |
||
dt |
|
|
xi |
||
|
|
|
|
Отметим, что используя функцию H , векторное уравнение (2.1) может быть записано в виде системы
dxi |
|
H (x, ψ, u) |
, |
i 1,2,..., n. |
dt |
|
i |
||
|
|
|
||
|
|
|
|
Теорема 2.1 (принцип максимума Понтрягина для задачи быстродей-
ствия). Пусть u(t) , t t0 ,t1 , - оптимальное (по быстродействию) управление, x(t) - соответствующая траектория уравнения (2.1), удовлетворяющая условиям x(t0 ) x0 , x(t1 ) x1 . Тогда существует ненулевая непрерывная вектор-функция ψ(t) , являющаяся решением системы уравнений (2.2), соответствующей функ-
циям x(t) и u(t) , такая, что для любого t t0 ,t1 и для любой точки v |
выпол- |
няется неравенство |
|

20
H (x(t), ψ(t), u(t) H (x(t), ψ(t), v). |
(2.3) |
Неравенство (2.3), составляющее центральный пункт теоремы 2.1, дало основание назвать эту теорему принципом максимума.
Линейная задача быстродействия. Рассмотрим частный случай задачи об оптимальном быстродействии, когда уравнение состояния (2.1) линейно по управлению и состоянию, то есть управляемая система имеет вид
|
dx |
Ax |
Bu |
, |
(2.4) |
|
|
|
|
||||
|
dt |
|||||
|
|
|
|
|
||
где A – матрица размера n n, B – матрица размера n m . |
Нужно найти опти- |
|||||
мальное управление со значениями из |
, |
которое переводит систему (2.4) из |
||||
состояния x0 в фазовое состояние x1 |
за кратчайшее время. |
|
||||
В случае линейного уравнения состояния гамильтониан принимает вид |
||||||
H (x, ψ,u) |
ψ, Ax |
ψ, Bu . |
(2.5) |
|||
Здесь первое слагаемое не зависит от управления. Система (2.2) для сопряженной переменной записывается в данном случае следующим образом:
dψ |
AT ψ , |
(2.6) |
|
dt
где, как обычно, AT означает транспонированную к A матрицу.
Из теоремы 2.1. и вида гамильтониана (2.5) следует
Теорема 2.2 (принцип максимума Понтрягина для линейной задачи быст-
родействия). Пусть u(t) , t t0 ,t1 , - оптимальное управление для линейной задачи быстродействия, x(t) - соответствующая траектория уравнения (2.1), удовлетворяющая условиям x(t0 ) x0 , x(t1 ) x1 . Тогда существует ненулевая непрерывная вектор-функция ψ(t) , являющаяся решением уравнения (2.6), такая, что для любого t t0 ,t1  и для любой точки v
и для любой точки v 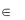 выполняется неравенство
выполняется неравенство
 ψ(t), Bv
ψ(t), Bv
 ψ(t), Bu(t)
ψ(t), Bu(t) .
.
2.2. Практическая часть
Задача 2. Найти оптимальное управление, которое переводит систему (2.4) из состояния x 0 в начало координат за кратчайшее время при условии u t 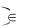 .
.
