
4639
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный лесотехнический университет имени Г.Ф. Морозова»
МОДЕЛИРОВАНИЕ ТРАНСПОРТНЫХ ПРОЦЕССОВ
Методические указания к практическим занятиям для студентов по направлению подготовки 23.03.01 Технология транспортных процессов
Воронеж 2018
2
УДК 656.13
Лихачев Д. В. Моделирование транспортных процессов [Электронный ресурс]: методические указания к практическим занятиям для студентов по направлению подготовки 23.03.01 Технология транспортных процессов / Д.В. Лихачев, Ю.В. Струков, Р.А. Сподарев; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ им. Г.Ф. Морозова». – Воронеж, 2018. – 44 с.
Печатается по решению учебно-методического совета |
|
ФГБОУ ВО «ВГЛТУ им. Г.Ф. Морозова» (протокол № ... от ............ |
г.) |
Рецензент: заведующий кафедрой электротехники и автоматики ФГБОУ ВО «Воронежский государственный аграрный университет имени императора Петра I» д-р техн. наук, проф. Д.Н. Афоничев.
3
ОГЛАВЛЕНИЕ |
|
ВВЕДЕНИЕ …………………………………………………………………... |
3 |
1. Практическое занятие № 1. Классическая транспортная задача.............. |
5 |
1.1. Математическая постановка классической транспортной задачи … |
5 |
1.2. Решение классической транспортной задачи в Excel ........................ |
7 |
1.3. Задачи для самостоятельного решения ............................................... |
11 |
1.4. Содержание отчета по практической работе № 1 .............................. |
14 |
1.5. Контрольные вопросы к практической работе № 1 ........................ |
14 |
2.Практическое занятие № 2.Решение задачи поиска кратчайшего пути в Excel ……………………….............................................................................. 15
2.1.Математическая постановка задачи поиска кратчайшего пути …... 15
2.2.Решение задачи о нахождении кратчайшего пути в Excel ………… 17
2.3.Содержание отчета по практической работе № 2 .…………………. 20
2.4. Контрольные вопросы к практической работе № 2 ........................ |
21 |
3. Практическое занятие № 3. Транспортная задача с промежуточными |
|
пунктами .......................................................................................................... |
23 |
3.1. Математическая постановка транспортной задачи с промежуточными |
|
пунктами ................................................................................................. |
23 |
3.2. Решение транспортной задачи с промежуточными пунктами в Excel .. |
26 |
3.3.Содержание отчета по практической работе № 3 ………………….. 28
3.4.Контрольные вопросы к практической работе № 3 ..………….…... 29
4. Практическое занятие № 1. Задача о назначениях....................................... |
31 |
4.1.Математическая постановка задачи о назначениях ..…………......... 31
4.2.Решение задачи о назначениях в Excel ……………………..………. 33
4.3.Содержание отчета по практической работе № 4 ………………….. 39
4.4.Контрольные вопросы к практической работе № 4 ..………….…... 41 Заключение ……………………………………………………………………... 42 БИБЛИОГРАФИЧЕСКИЙ СПИСОК……………………………………….... 43
4
ВВЕДЕНИЕ
Важнейшей задачей при подготовке бакалавров по направлению подготовки 23.03.01 (190700.62) – Технология транспортных процессов является обучение студентов практически значимым методам моделирования транспортных сетей. Эти методы позволяют проектировать транспортные процессы, которые осуществляются с минимальными затратами трудовых и материальных ресурсов при обеспечении высокого качества выполнения доставки грузов.
При выполнении практических работ студенты должны освоить методы оптимизации на сетях и графах, методы линейного программирования и другие методы оптимизации транспортных процессов с использованием современных компьютерных технологии.
Практикум содержит 4 практические работы, по каждой из которых студенты должны подготовить отчет согласно индивидуальному варианту. Для самостоятельного контроля знаний после каждой практической работы предусмотрены контрольные вопросы.
Практикум предназначен для студентов всех форм обучения обучающихся по направлению подготовки 23.03.01 (190700.62) – Технология транспортных процессов при изучении ими дисциплины Б1.В.ОД.15 – Моделирование транспортных процессов.
5
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1. КЛАССИЧЕСКАЯ ТРАНСПОРТНАЯ ЗАДАЧА
Цель работы: изучить модели классической транспортной задачи, как частный случай модели линейного программирования, освоить надстройку Поиск решения в Excel, научиться применять данные модели для решения практических задач в области организации перевозок и управления на автомобильном транспорте.
1.1. Математическая постановка классической транспортной задачи
В исследовании операций под транспортной задачей обычно понимают задачу выбора плана перевозок некоторого товара (изделий, груза) от m источников (пунктов производства, поставщиков) к n стокам (станциям назначения, пунктам сбыта), обеспечивающего минимальные транспортные затраты. При этом предполагают, что мощность i-го источника (объем поставок товара от i-го источника) равна Si > 0, i = 1, ..., m; мощность j-го стока (объем поставок товара к j-му стоку) равна Dj > 0, j = 1, ..., n; стоимость перевозки единицы товара (в условных денежных единицах) от i-го источника к j-му стоку равна сij, суммарная мощность всех источников равна суммарной мощности всех стоков, т. е. /1/
m
Si
i 1
n |
|
D j . |
(1.1) |
j 1
Далее под объемом товара будем понимать его количество в фиксированных единицах измерения.
Для математического описания транспортной задачи вводят переменные хij, обозначающие объемы поставок товара от i-го источника к j-му стоку. В этом случае xi1 + xi2 + … + xin – общий объем поставок товара от i- го источника, то есть мощность этого источника; x1j + x2j + … + xmi – общий объем поставок товара к j-му стоку, то есть мощность этого стока; c11x11 + c12x12 + … + cmnxmn – суммарная стоимость перевозок товара от ис-
6
точников к стокам. С учетом этого рассматриваемая задача может быть представлена в следующем виде /1/
m n |
|
|
|
cijxij min |
|
||
i 1 j 1 |
|
|
|
n |
|
|
|
xij |
Si |
|
|
j 1 |
|
|
|
m |
|
|
(1.2) |
|
. |
||
xij |
D j |
|
|
i 1 |
|
|
|
xij 0 |
|
|
|
xij N 0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Последнее ограничение означает, что объемы поставок являются натуральными (то есть целыми числами) включая ноль. Это ограничение необязательно и зависит от формулировки задачи.
На рисунке 1.1 показано представление транспортной задачи в виде сети с m пунктами отправления и n пунктами назначения, которые показаны в виде узлов сети. Дуги, соединяющие узлы сети, соответствуют маршрутам, связывающим пункты отправления и назначения. С дугой (i, j), соединяющей пункт отправления i с пунктом назначения j, соотносятся два вида данных: стоимость сij перевозки единицы груза из пункта i в пункту и количество перевозимого груза хij. Объем грузов в пункте отправления i равен Si, а потребность в пункте назначения j равна Dj. Задача состоит в определении неизвестных величин хij, минимизирующих суммарные транспортные расходы и удовлетворяющих ограничениям, накладываемым на объемы грузов в пунктах отправления (предложение) и потребности пунктах назначения (спрос).
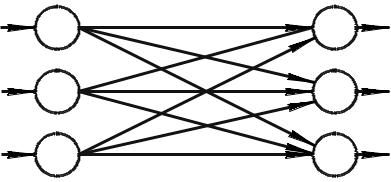
7
Предложение |
Спрос |
|||
S1 |
1 |
c11x11 |
1 |
D |
|
|
1 |
||
S2 |
2 |
|
2 |
D |
|
|
2 |
||
Sm |
m |
|
n |
D |
|
cmnxmn |
n |
||
|
|
|
|
|
Рис. 1.1 – Представление транспортной задачи в виде сети
1.2. Решение классической транспортной задачи в Excel
Рассмотрим решение классической транспортной задачи на основе примера, заимствованного из книги Хэмди А. Таха /2/. Из того же источника взяты задачи для самостоятельного решения, представленные в конце пункте 1.3.
Пример 1.1. Автомобильная компания «MG Auto» имеет три завода
вЛос-Анджелесе, Детройте и Новом Орлеане и два распределительных центра, в Денвере и Майами. Объемы производства заводов компании в следующем квартале составят соответственно 1000, 1500 и 1200 автомобилей. Ежеквартальная потребность распределительных центров составляет 2300 и 1400 автомобилей.
Расстояния между заводами и распределительными центрами приведены
втаблице 1.1.
Таблица 1.1
Расстояния между заводами и распределительными центрами, мили
Поставщик |
|
Потребитель |
|
|
|
|
|
|
Денвер |
|
Майами |
Лос-Анджелес |
1000 |
|
2690 |
Детройт |
1250 |
|
1350 |
|
|
|
|
Новый Орлеан |
1275 |
|
850 |
|
|
|
|
8
Транспортная компания оценивает свои услуги в 8 центов за перевозку одного автомобиля на 1 милю. В результате получаем представленную в таблице 1.2 стоимость перевозок (с округлением до 1 долл.) по каждому маршруту.
|
|
|
|
Таблица 1.2 |
|
|
Стоимость перевозок, долл. |
|
|
||
|
|
|
|
|
|
Поставщик |
|
Потребитель |
|
|
|
|
|
|
|
|
|
|
Денвер |
|
Майами |
|
|
|
|
|
|
||
Лос-Анджелес |
|
80 |
|
215 |
|
Детройт |
|
100 |
|
108 |
|
|
|
|
|
|
|
Новый Орлеан |
|
102 |
|
68 |
|
|
|
|
|
|
|
Основываясь на данных таблицы 1.2, формулируем следующую задачу линейного программирования. Минимизировать
F = 80∙х11 + 215∙х12 + 100∙х21 + 108∙х22 + 102∙х31 + 68∙х32 → min,
при ограничениях
x11 x12 |
1000 (Лос Анжелес) |
||||||||
x 21 x 22 |
1500 (Детройт ) |
|
|||||||
|
|||||||||
x31 x32 |
1200 (Новый Орлеан) |
||||||||
x11 x 21 |
x31 2300 (Денвер) |
. |
|||||||
|
|||||||||
x |
21 |
x |
22 |
x |
32 |
1400 (Майами) |
|||
|
|
|
|
|
|
||||
x |
|
0, i 1, 2, 3, |
j 1, 2. |
||||||
ij |
|
||||||||
|
|
|
|
|
|
|
|
|
|
(1.3)
(1.4)
Эти ограничения выражены в виде равенств, нескольку общий объем произведенных автомобилей (S = 1000 + 1500 + 1200 = 3700) равен суммарному спросу распределительных центров (D = 2300 + 1400 = 3700).
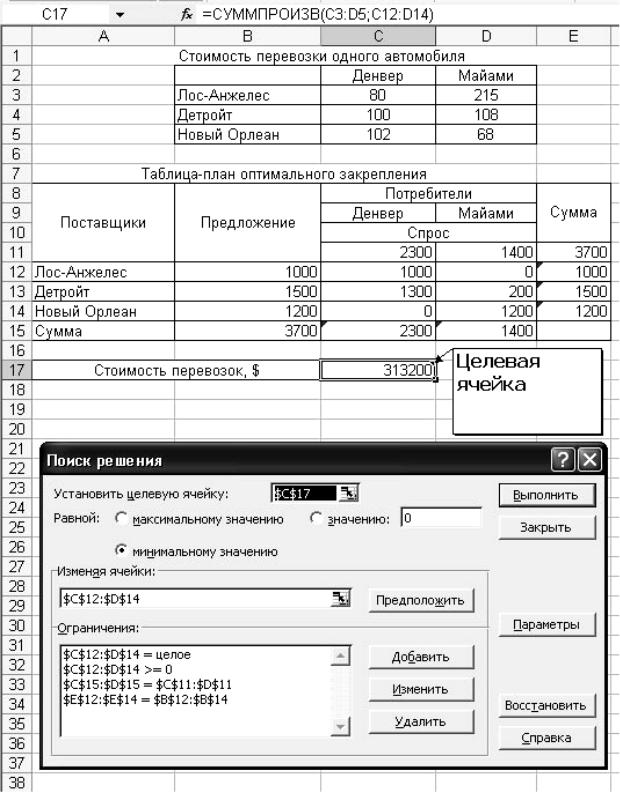
Данную задачу можно решить симплекс-методом /2, 3/ или с помощью так называемой транспортной таблицы. Решение данной задачи в Excel представлено на рисунке 1.2.
9
Исходные данные для решения классической транспортной задачи целесообразно представить в виде двух таблиц, в первой из которых представлены значения стоимости перевозок единицы товара сij от i-го поставщика к j- му потребителю. Во второй таблице представлены значения Si предложения каждого i-го поставщика; значения Dj, спроса каждого j-го потребителя, переменные хij, первоначально принимающие нулевые значения; вспомогательная строка и вспомогательный столбец Сумма. Целевая ячейка С17 должна содержать формулу, выражающую целевую функцию /1, 2/
=СУММПРОИЗВ (C3:D5;C12:D14) |
(1.5) |
Используя меню Сервис Поиск решения, открываем диалоговое окно Поиск решения, в котором устанавливаем целевую ячейку равной минимальному значению, определяем диапазон изменяемых ячеек и ограничения и запускаем процедуру вычисления, щелкнув по кнопке Выполнить.
Оптимальное решение данной задачи предполагает перевозку 1000 автомобилей из Лос-Анджелеса в Детройт, 1300 автомобилей – из Детройта в Денвер, 200 автомобилей – из Детройта в Майами и 1200 – из Нового Орлеана в Майами. Минимальная стоимость перевозок составляет $ 313200.
Когда суммарный объем предложений (грузов, имеющихся в пунктах отправления) не равен общему объему спроса на товары (грузы), запрашиваемые пунктами назначения, транспортная задача называется несбалансированной. В этом случае при решении классической транспортной задачи методом потенциалов применяют прием, позволяющий несбалансированную транспортную задачу сделать сбалансированной. Для этого вводят фиктивные пункты назначения или отправления.
10
Рис. 1.2. Решение классической транспортной задачи
Выполнение баланса транспортной задачи необходимо для того, чтобы иметь возможность применить алгоритм решения, построенный на использовании транспортных таблиц. В Excel несбалансированная транспортная задача
