
4566
.pdf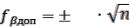
11
2. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА ТЕОДОЛИТНЫХ ХОДОВ
2.1. Уравнивание углов полигона
При математической обработке полевых измерений из полевого журнала записываются в ведомость вычисления координат (табл. 2), значения углов полигона в графу 3, а меры линий в графу 6. Вычисляют сумму углов графы 3 и записывают ее в этой же графе внизу. Затем вычисляют угловую невязку fβ по формуле
n
где изм
1
теор
|
n |
|
f |
изм теор , |
(1) |
|
1 |
|
– сумма измеренных углов (практическая);
– теоретическая сумма углов для полигона. |
|
теор = 180º·(n - 2), |
(2) где |
n – число углов в полигоне. |
|
|
|
|
|
|
В нашем примере (табл. 2) |
f = + 0°01,5'. Полученную невязку необхо- |
|||||
димо сравнить с допустимой, которая вычисляется по формуле |
|
|||||
|
|
|
1΄ |
. |
(3) |
|
Если фактическая невязка допустима, т.е. f изм f доп , |
тогда ее распре- |
|||||
деляют на каждый угол по формуле |
|
|
||||
|
|
f |
|
|
|
|
|
|
|
||||
|
|
n |
|
(4) |
||
|
|
|
|
|||
Исправленное значение угла |
' |
вычисляют по формуле (5) |
и записывают в |
|||
графу 3 |
|
|
|
|
|
|
' |
|
(5) |
|
||
|
|
Сумма всех поправок для углов должна равняться невязке, взятой с обратным знаком, а сумма исправленных углов – ее теоретическому значению. Полученная невязка очень редко делится на п без остатка. Тогда возникает необходимость в одни углы вводить большие поправки, чем в другие. Так как углы, заключенные между короткими сторонами, измеряются с большей погрешностью (вследствие погрешностей центрирования и визирования теодолита), чем углы, заключенные между длинными сторонами, то большие поправки вводят в углы, заключенные между короткими сторонами. Поэтому в нашем примере углы при точках 1, 3 получили большие поправки, округленные до целых минут.
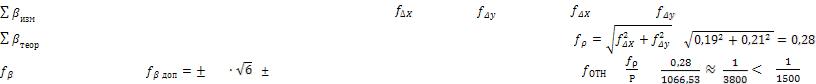
12
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
||
|
|
|
|
Ведомость вычисления координат вершин теодолитного хода |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
№ то |
Внутренние углы |
Дирек- |
Румбы |
Длины |
Приращение вычислен- |
|
Приращения исправлен- |
|
Координаты |
|
|
|||||||||||
чек |
|
|
ционные |
линий |
линий |
|
|
ные |
|
|
ные |
|
|
|
|
|
|
|
|
|
|
|
|
Измерен- |
Исправ- |
углы |
|
|
± |
Х |
|
± |
У |
|
± |
Х |
|
± |
|
У |
± |
Х |
± |
У |
|
|
ные |
ленные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
9 |
10 |
|
11 |
12 |
|
13 |
|
14 |
15 |
16 |
17 |
18 |
|
1 |
-01΄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
1000,00 |
+ |
1000,00 |
|
|
126°14΄ |
126° 13΄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
38 °15 ΄ |
св: 38° 15΄ |
201,39 |
+ |
-0,03 |
|
+ |
-0,04 |
|
+ |
158,12 |
|
+ |
|
124,64 |
|
|
|
|
|
|
|
|
|
|
|
|
158,15 |
|
|
124,68 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
124° 56 ΄ |
124° 56΄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
1158,12 |
+ |
1124,64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
93° 19΄ |
юв:86° 41΄ |
158,09 |
- |
-0,03 |
|
+ |
-0,03 |
|
- |
9,18 |
|
+ |
|
157,79 |
|
|
|
|
|
|
|
|
|
|
|
|
9,15 |
|
|
157,82 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
-0,5΄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
1148,94 |
+ |
1282,43 |
12 |
|
105 °07,5΄ |
105° 07΄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
168° 12΄ |
юв:11° 48΄ |
156,00 |
- |
-0,03 |
|
+ |
-0,03 |
|
- |
152,73 |
|
+ |
|
31,87 |
|
|
|
|
|
|
|
|
|
|
|
|
152,70 |
|
|
31,90 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
146° 35 ΄ |
146° 35΄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
996,21 |
+ |
1314,30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
201° 37΄ |
юз : 21° |
192,85 |
- |
-0,03 |
|
- |
-0,04 |
|
- |
179,32 |
|
- |
|
71,08 |
|
|
|
|
|
|
|
|
|
37΄ |
|
|
179,29 |
|
|
71,04 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
101° 32΄ |
101° 32΄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
816,89 |
+ |
1243,22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
280° 05΄ |
сз : 79° 55΄ |
205,40 |
+ |
-0,04 |
|
- |
-0,04 |
|
+ |
35,92 |
|
- |
|
202,27 |
|
|
|
|
|
|
|
|
|
|
|
|
35,96 |
|
|
202,23 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
115° 37΄ |
115° 37΄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
852,81 |
+ |
1040,95 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
344° 28΄ |
сз : 15° 32 ΄ |
152,80 |
+ |
-0,03 |
|
- |
-0,03 |
|
+ |
147,19 |
|
- |
|
-40,95 |
|
|
|
|
|
|
|
|
|
|
|
|
147,22 |
|
|
40,92 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
1000,00 |
+ |
1000,00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=720°01,5΄ |
|
|
Р=1066,53 |
|
=+0,19 |
|
=+0,21 |
|
= 0 |
|
|
= 0 |
|
|
|
|
|
||||
|
=720°00΄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
=+0°01,5΄ |
|
1 ΄ |
= 0°02,4΄ |
|
|
|
|
|
|
|
|
= |
|
= |
|
|
|
|
|
|||
13
2.2. Вычисление дирекционных углов и румбов сторон хода
Для получения координат точек полигона нужно знать дирекционные углы и горизонтальные проложения линий. Зная дирекционный угол одной линии, можно вычислить дирекционные углы всех остальных линий полигона.
Внашем примере (табл. 2) в качестве исходного взят дирекционный угол
1 2 = 38°15' линии 1–2, условно равный магнитному азимуту.
Дирекционные углы сторон Si теодолитного хода (i =1, 2, ...,n) вычисляют
по формуле |
i |
i 1 |
180 i |
, |
|
|
(6) |
||||
|
|
|
|
|
где i – дирекционный угол последующей линии;i 1 – дирекционный угол предыдущей линии;
i – исправленный внутренний угол полигона, лежащий справа по ходу. Для нашего примера
2 3 1 2 180 2 38 15' 180 124 56 93 19'.
Последовательно вычисляя дирекционные углы остальных сторон хода, должны получить исходный дирекционный угол, т.е.
1 2 6 1 180 1 344 28' 180 126 13' 38 15'.
Это служит контролем вычисления дирекционных углов. Вычисленные дирекционные углы переводят в румбы линий полигона, записывают в графу 5, исходя из следующих зависимостей:
I чечверть |
СВ |
r , |
(а 0о 90о ), |
|
II четверть |
ЮВ r 180 , |
( 90 180 ), |
|
|
III четверть ЮЗ |
r 180 , |
( 180 270 ), |
(7) |
|
IV четверть |
СЗ |
r 360 , |
( 270 360 ). |
|
где r – румб (угол),
– дирекционный угол.
2.3. Вычисление горизонтальных проложений линий и расстояний, недоступных для измерения мерной лентой
Для изображения фигуры местности на горизонтальной плоскости следует знать горизонтальные проложения ее сторон. Их вычисляют по формуле
14 |
|
S S'cos , |
(8) |
где S – горизонтальное проложение линии, м; |
|
S' – измеренное наклонное расстояние линии, м; |
|
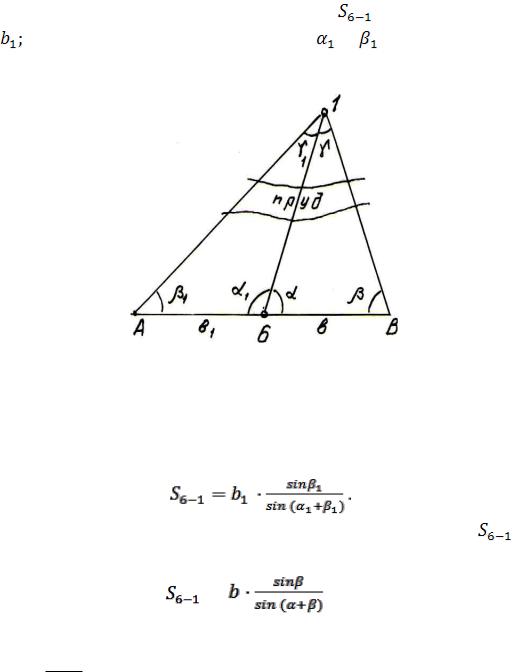
В практике встречаются случаи, когда линию нельзя измерить лентой из-за препятствий, пересекаемых линией, – река, болото, овраг и т.д. На рис. 2 приведен наиболее часто встречающийся случай.
Для определения недоступного расстояния |
измеряют: мерной лентой |
|
- базис |
теодолитом - горизонтальные углы |
и . |
Рис. 2. Схема определения расстояний, недоступных для измерения мерной лентой
Значение искомого расстояния вычисляют по теореме синусов:
|
|
(9) |
Для контроля измеряют базис b, углы |
α и β и вычисляют |
по- |
вторно по формуле |
|
|
= |
. |
(10) |
Относительное расхождение в двух вычислениях 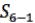 допускается не
допускается не
1
более 1000 .
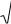
15
2.4. Вычисление и уравнивание приращений координат
Приращения координат X и |
Y сторон хода находят по формулам |
|
||||
X iпр. |
|
|
|
|
||
Si cos i ri , |
(11) |
|||||
Yiпр. |
|
|
|
|||
Si sin i ri . |
(12) |
|||||
Знаки каждого приращения зависят от направления линии и определяются в зависимости от величины дирекционных углов или названий четвертей румбов. Для определения знаков приращений координат можно пользоваться данными табл. 3.
|
|
|
|
Таблица 3 |
|
|
|
Знаки приращений координат |
|
|
|
|
|
|
|
|
|
|
Название румба линии |
Знаки приращений |
|||
|
|
|
|
|
|
|
|
|
X |
Y |
|
|
|
|
|
|
|
|
Северо-восток (СВ) |
+ |
+ |
|
|
|
|
|
|
|
|
|
Юго-восток (ЮВ) |
– |
+ |
|
|
|
|
|
|
|
|
|
Юго-запад |
(ЮЗ) |
– |
– |
|
|
|
|
|
|
|
|
Северо-запад |
(СЗ) |
+ |
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
Знаки приращений записывают в графы 7 и 9, а абсолютные их значения
– в графы 8 и 10 (табл. 2). Невязки в приращениях координат находят по формулам
n |
|
n |
|
|
X i теор . |
0, |
Yi теор. |
0. |
(13) |
i 1 |
|
i 1 |
|
|
Алгебраическая сумма приращений координат в полигоне по каждой оси должна быть равна нулю, отличие от нуля и будет являться фактической невязкой, следовательно
|
n |
|
|
f x |
X i |
|
|
|
i 1 |
|
|
|
. |
(14) |
|
|
n |
||
|
|
|
|
f y |
Yi |
|
|
|
i 1 |
|
|
Абсолютную величину линейной невязки хода подсчитывают по формуле
|
|
|
|
|
|
|
f |
|
f 2 |
f 2 |
(15) |
||
|
абс |
|
|
Y . |
|
|
16
Относительная невязка (в периметре) теодолитного полигона считается
|
|
|
|
1 |
|
|
|
n |
|
допустимой, если она не превышает |
|
|
|
|
|
периметра |
Si , т.е. |
||
1500 |
|
||||||||
|
|
|
|
|
i 1 |
||||
|
fs |
|
|
1 |
|
|
|
||
|
n |
1500 |
|
(16) |
|||||
|
|
|
|
||||||
|
Si |
|
|
|
|
|
|
|
|
i 1
Если невязка в периметре fS оказалась допустимой, то невязки по осям координат f x и f y распределяют с обратным знаком пропорционально гори-
зонтальным проложениям линий согласно отношению
f
X1 |
|
|
|
x |
Si ; |
(17) |
|
|
|
n |
|||||
|
|
Si |
|
|
|
||
|
|
|
i 1 |
|
|
|
|
Y1 |
|
|
f |
|
|
|
|
|
y |
|
Si . |
(18) |
|||
|
|
|
|||||
|
n |
|
|||||
|
|
|
|
Si |
|
||
|
|
|
|
i 1 |
|
|
|
Например, поправка в приращении |
линии 1–2 по |
оси абсцисс будет |
|||||
(табл.2)
X1 0,03 м .
Суммы поправок в приращениях по каждой оси должны быть равны
n
X1 f x ; (19)
i 1
n
Y1 f y , (20)
i 1
то есть соответствующим невязкам по осям координат, взятым с обратными знаками.
Уравненные приращения координат X i , Yi находят по формулам
X |
iисп. |
X |
iпр. |
|
; |
(21) |
||
|
|
|
X i |
|
||||
Y |
|
Y |
|
. |
|
(22) |
||
iисп. |
|
iпр. |
|
Yi |
|
|
||
Полученные значения записывают в графы 12 и 14. Алгебраические суммы уравненных приращений должны быть равны нулю (табл. 2).
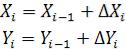
17
2.5. Вычисление координат точек полигона
Для вычисления координат точек полигона необходимо знать координаты одной точки полигона. Координаты исходной точки получают путем привязки к пунктам опорной геодезической сети. Если геодезическая привязка не производилась, то одной точке полигона дают условные координаты X и Y. В
нашем примере координаты первой точки приняты равными |
|
|||
|
Х1 = 1000,00 м, |
Y1 = 1000,00 м. |
|
|
Плоские прямоугольные координаты остальных точек полигона вычис- |
||||
ляют по формулам: |
|
|
|
|
|
|
|
; |
(23) |
|
|
|
. |
(24) |
Например |
X 2 |
X 1 X iисп. 1000,00 158,12 1158,12( м ) , |
|
|
|
Y2 |
Y 1 Yiисп. 1000,00 124,64 1124,64( м ) . |
|
|
При их вычислении должны получиться координаты конечного исходного пункта, что служит контролем правильности вычислений.
3. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА ТЕОДОЛИТНОГО ХОДА, ПРОЛОЖЕННОГО МЕЖДУ ДВУМЯ ПУНКТАМИ
(диагональный ход)
Диагональный теодолитный ход увязывают в той же последовательности, как и замкнутый. На рис. 1 показан диагональный ход, примыкающий к двум сторонам 3-4 и 6-1 замкнутого полигона. При этом измерялись правые (по ходу) горизонтальные углы.
Математическую обработку выполняют в следующем порядке:
1. В графу I (табл. 4) выписывают номера всех точек по ходу, начиная с исходной (точка 4) и кончая точкой 6. Пример на увязку хода 4-8-7-6 приведен в табл. 4 .
Исходными данными для обработки диагонального хода являются дирекционные углы 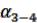 и
и 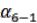 и координаты точек 4 и 6.
и координаты точек 4 и 6.
2.В графу 2 табл. 4 выписывают углы по ходу, начиная и кончая примычными углами, измеренными при начальной и конечной точках, и подсчитывают сумму углов.
3.В графу 4 по направлению хода вписывают дирекционные углы исходных линий.

18
4. При уравнивании углов их фактическую невязку определяют по фор-
муле
где |
измеренные горизонтальные углы; |
- дирекционный угол на- |
||
чальной линии ; |
- дирекционный угол конечной лини; n - число углов в |
|||
ходе, включая примычные. |
|
|
||
|
В нашем примере |
= -0°02'. |
|
|
|
Полученную невязку сравнивают с допустимой. |
|||
|
Так как теодолитный |
ход опирается на дирекционные углы ранее проло- |
||
женных ходов, то на угловую невязку хода, помимо погрешностей измерений углов, влияют погрешности исходных дирекционных углов, поэтому допустимую угловую невязку определяют по формуле
|
. |
(26) |
В нашем примере |
= 0°04΄. |
|
Угловые поправки |
распределяют так же, как и в полигоне, на все углы |
|
хода.
5.Вычисляют дирекционные углы, а затем румбы сторон хода так же, как
ив замкнутом полигоне. Контролем правильности уравнивания углов служит получение дирекционного угла конечной линии. В нашем примере 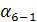 = =344°28΄.
= =344°28΄.
6.Вычисляют горизонтальные проложения линий и записывают в графу 6
табл. 4 .
7.Вычисляют приращения координат по формулам (11, 12).
8.Невязки в приращениях координат 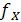 и
и 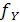 вычисляют по формулам
вычисляют по формулам
(27)
.
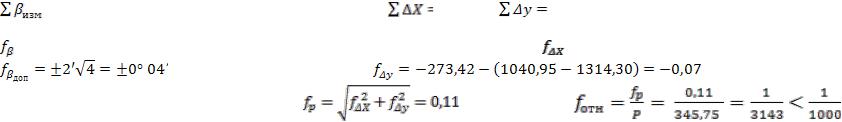
19
Таблица 4
Ведомость вычисления координат вершин теодолитного хода (диагональный ход)
№ |
Внутренние углы |
Дирек- |
Румбы |
Длины |
|
Приращения |
|
Приращения |
|
Координаты |
|
|||||||
то |
|
|
ционные |
линий |
линий |
|
вычисленные |
|
исправленные |
|
|
|
|
|
||||
чек |
Измерен- |
Исправ- |
углы |
|
|
± |
Х |
± |
У |
± |
Х |
± |
У |
± |
Х |
± |
У |
|
|
ные |
ленные |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
3 |
+01΄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
68° 17΄ |
68° 18΄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
168° 12΄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
+01΄ |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
996,21 |
+ |
1314,30 |
|
|
243° 37΄ |
243° 38΄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
279°54΄ |
Сз:80° 06΄ |
115.65 |
+ |
19,88 |
+ |
113,93 |
+ |
19,91 |
+ |
113,91 |
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
165° 36΄ |
165° 36΄ |
|
|
|
|
|
|
|
|
|
|
|
+ |
1016,12 |
+ |
1200,39 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
216°16΄ |
Юз36° 16΄ |
101.60 |
- |
81,92 |
- |
60,10 |
- |
81,90 |
- |
60,08 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
165° 36΄ |
165° 36΄ |
|
|
|
|
|
|
|
|
|
|
|
+ |
934,22 |
+ |
1140,31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
230°40΄ |
Юз50° 40΄ |
128.50 |
- |
81,44 |
- |
99,39 |
- |
81,41 |
- |
99,36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
66 °12΄ |
66 °12΄ |
|
|
|
|
|
|
|
|
|
|
|
+ |
852,81 |
+ |
1040,95 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
344°28΄ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=543°42΄ |
|
|
P=345,75 |
|
- 143,48 |
|
-273,42 |
|
|
|
|
|
|
|
|
||
=543°42΄- (168°12΄- 344°28΄+180°· 4)= -0° 02΄ |
|
|
|
|
= -143,48-(852,81-996,21) = - 0,08 |
|
|
|
|
|||||||||
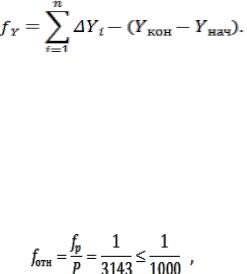
20
(28)
В нашем примере
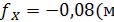 );
);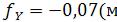 ).
).
Абсолютную невязку вычисляют по формуле (15)
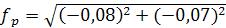 =0,11(м).
=0,11(м).
Затем вычисляют относительную невязку и сравнивают ее с допустимой невязкой, определяемой по формуле
(29)
где P - длина хода от начальной до конечной точки.
Если невязка допустима, то ее распределяют пропорционально длинам линий хода по формулам (17, 18). Уравненные приращения координат записывают в графы 12 и 14 табл 4.
9. Последовательно вычисляют координаты всех точек разомкнутого хода по формулам (23, 24).
4. ПОСТРОЕНИЕ ПЛАНА
4.1. Построение прямоугольной координатной сетки
Построение координатной сетки выполняют на листе плотной чертёжной бумаги. При оформлении плана небольших участков местности сетку квадратов можно разбить следующим простым способом. С угла на угол листа бумаги тонко очиненным карандашом проводят две диагонали.
Из точки пересечения диагоналей откладывают циркулем-измерителем четыре равных отрезка. Соединив концы отрезков прямыми линиями, получают прямоугольник, который служит основой для последующей разбивки координатной сетки. На сторонах прямоугольника при помощи циркуля-измерителя откладывают отрезки длиной 5 см.
Соединив линиями соответствующие точки противоположных сторон прямоугольника, получают сетку квадратов. Правильность построения сетки проверяют сравнением диагоналей квадратов и длин их сторон.
Расхождения сторон квадратов не должны превышать ±0,2 мм. Линии ко-
