
4553
.pdf
31
вместо знака можно писать знак арифметического сложения: А+В. Этим знаком мы и будем пользоваться в дальнейшем.
Дизъюнкция, называемая иногда логическим сложением, определяется следующими аксиомами:
0+0=0; |
1+0=1; |
0+1=1; |
1+1=1. |
Конъюнкция обозначается знаком , но т.к. конъюнкция – «родня» арифметическому умножению, то вместо знака будем использовать точку, либо вообще не указывать никакого знака: А В = А·В = АВ.
Конъюнкция (логическое умножение) определяется следующими
аксиомами: |
|
0·0=0; |
1·0=0; |
0·1=0; |
1·1=1. |
Инверсия, или отрицание обозначается |
чертой над буквой: , и |
определяется следующими аксиомами: |
|
= 1; |
= 0. |
Рассмотрим следующие основные свойства:
а) операции дизъюнкции и конъюнкции обладают свойством
коммутативности:
|
А + В = В + А; |
АВ = ВА; |
б) |
операции дизъюнкции и |
конъюнкции обладают свойством |
ассоциативности: |
|
|
|
(А + В) + С = А + (В + С); |
(АВ)С = А(ВС), |
что позволяет удалять скобки во всех случаях, когда знаками дизъюнкции или
конъюнкции соединяются более двух переменных: |
|
(А + В) + С = А + В + С; |
(АВ)С = АВС; |
в) конъюнкция дистрибутивна относительно дизъюнкции: А(В + С) = АВ + АС,

32
что позволяет раскрывать скобки в выражениях и выносить общий множитель за скобки, например:
А(В + С + D + Е) = AB + AC + AD + AE,
АВС + ABD + ABEF = AB(C + D + EF);
г) дизъюнкция дистрибутивна относительно конъюнкции:
А + ВС = (А + В)(А + С); А + BCD = (A + B)(A + C)(A + D);
д) |
операции дизъюнкции и |
конъюнкции обладают свойством |
идемпотентности: |
|
|
|
А + А = А; |
А·А = А. |
Список теорем одной переменной имеет вид: |
||
|
; |
; |
|
; |
; |
|
; |
; |
|
; |
; |
 ,
,
где последняя теорема отражает свойство инволюции.
Булевы формулы могут быть записаны в виде суммы либо в виде произведения каких-либо выражений. В первом случае говорят о
дизъюнктивной форме, во втором – о конъюнктивной. Например,
выражения
Представлены в дизъюнктивной форме, а выражения
– в конъюнктивной.
Если булева формула записана в виде суммы выражений, каждое из которых представляет собой либо отдельный аргумент (с отрицанием или без отрицания), либо произведение некоторых аргументов, то эта формула является представленной в дизъюнктивной нормальной форме (ДНФ). Например,
выражения

|
33 |
представлены в ДНФ, а формула |
к ДНФ не относится, так как |
второе слагаемое не является ни отдельным аргументом, ни произведением переменных.
Если булева формула записана в виде произведения выражений, каждое из которых представляет собой либо отдельный аргумент (с отрицанием или без отрицания), либо сумму некоторых аргументов, то эта формула является представленной в конъюнктивной нормальной форме (КНФ). Например,
выражения
записаны в КНФ, а формула
КНФ не является, поскольку в первой паре скобок содержится произведение  .
.
Выражение, представленное отдельным аргументом или его отрицанием либо суммой или произведением нескольких переменных, одновременно входит в класс ДНФ и КНФ. Например:
Теорема поглощения записывается в двух формах – дизъюнктивной и
конъюнктивной, соответственно: |
|
; |
. |
Выражение второе можно получить из первого, если знаки сложения и умножения поменять местами.
Теорема склеивания также имеет две формы – дизъюнктивную и конъюнктивную:
 ;
;
Теорема поглощения, как и теорема склеивания, применяется при упрощении булевых формул, например:
 ;
;
 ;
;
 .
.

34
Теорема де Моргана связывает все три основные операции булевой алгебры – дизъюнкцию, конъюнкцию и инверсию:
 ;
;
 .
.
Первая теорема читается так: отрицание произведения есть сумма отрицаний. Вторая: отрицание суммы есть произведение отрицаний.
Теорема де Моргана применима и к большему числу переменных:
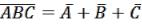 ;
;
 ;
;
 ;
;
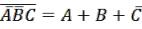 .
.
Булевы функции. Элементарные булевы функции
В общем случае функция – это некоторое правило (закон), согласно которому каждому элементу множества X, представляющего собой область значений независимого переменного x, ставится в соответствие определенный элемент множества F, под которым понимается область значений зависимого переменного f. В случае булевых функций  . Правилом, при помощи которого задается функция, может служить любая булева формула, например:
. Правилом, при помощи которого задается функция, может служить любая булева формула, например:
|
|
. |
Символом |
здесь обозначена |
функция, которая является, как и |
аргументы |
, двоичной переменной. |
|
Аргументы – это независимые переменные, они могут принимать любые |
||
значения – либо 0, либо 1. Функция же |
- зависимая переменная. Ее значение |
|
полностью определяется значениями переменных и логическими связями между ними.
Булевы функции можно задавать таблицами. В таблице перечисляются все возможные наборы значений аргументов, и для каждого набора указывается значение функции. Такую таблицу называют таблицей соответствия
(истинности).
Приведем обозначения, названия и таблицы, определяющие так называемые элементарные булевы функции.

35
1)Функции 0 и 1 называются соответственно тождественным нулем
итождественной единицей.
2)Функция  называется тождественной функцией и обозначается
называется тождественной функцией и обозначается
через  .
.
3)Функция 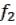 называется отрицанием
называется отрицанием  и обозначается
и обозначается  .
.
Таблица 4.1
|
0 |
1 |
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
1 |
|
|
|
|
|
1 |
0 |
1 |
1 |
0 |
|
|
|
|
|
4)Функция  называется конъюнкцией
называется конъюнкцией  и
и 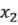 , обозначается
, обозначается  , или
, или  и часто читается «
и часто читается « ».
».
5)Функция  называется дизъюнкцией
называется дизъюнкцией 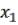 и
и  , обозначается
, обозначается 
ичасто читается «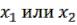 ».
».
6)Функция  называется суммой по модулю 2
называется суммой по модулю 2  и
и 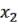 ,обозначается
,обозначается
 и часто читается «
и часто читается « плюс
плюс  » или «
» или « ».
».
7)Функция  называется эквивалентностью
называется эквивалентностью  и
и  , обозначается
, обозначается
~ |
или |
↔ |
и часто читается « |
эквивалентно |
» или |
« ».
».
8)Функция  называется импликацией
называется импликацией  и
и 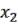 , обозначается
, обозначается  →
→
 и часто читается «
и часто читается « имплицирует
имплицирует  » или «
» или « ».
».
9)Функция  называется штрихом Шеффера
называется штрихом Шеффера  и
и  , обозначается
, обозначается
 │
│ и часто читается «
и часто читается « и
и 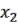 » или «
» или « ».
».
10) Функция |
называется стрелкой Пирса |
и , обозначается |
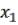 ↓
↓ и часто читается «
и часто читается «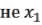 или
или  ».
».
Таблица 4.2
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
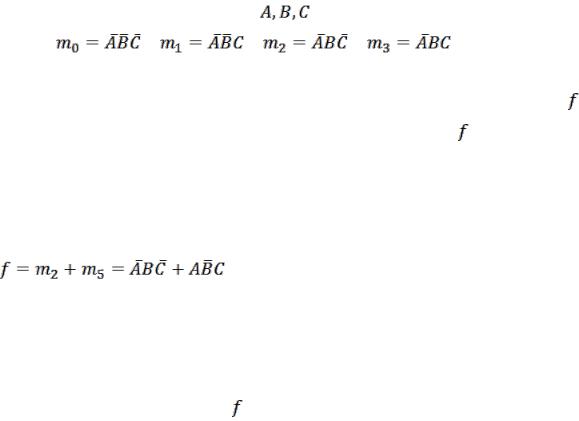
36
Совершенные дизъюнктивная и конъюнктивная нормальные формы
Функции, которые принимают единичное значение только на одном наборе, получили специальное обозначение. Называют их минимальными термами, а коротко – минтермами. Минтермом n переменных называется такое их произведение, в которое каждая переменная входит один раз (с отрицанием или без). Обозначаются минтермы буквой m с десятичным индексом, являющимся номером минтерма. Двоичный эквивалент номера минтерма – это набор, на котором минтерм принимает единичное значение. Например, если
функция зависит от трех аргументов |
, то |
|
|
, |
, |
, |
, и т.д. |
Если таблица соответствия содержит только одну единицу в колонке , то |
|||
функция представляет собой минтерм. Если же в колонке |
содержится две |
||
единицы (в различных строках), то функцию образует сумма соответствующих
минтермов. Такой случай представлен в табл. 4.3. |
|
|
|
|
|
||||||
В |
ней |
единицы |
расположены |
|
|
|
Таблица 4.3 |
||||
в строках |
2 и |
5, |
следовательно: |
|
|
|
|
|
|
||
№ |
A |
B |
C |
f |
|
||||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|||||
Аналогично рассуждая, придем к |
1 |
0 |
0 |
1 |
0 |
|
|||||
|
|
|
|
|
|
|
|||||
выводу о том, что в функцию может |
2 |
0 |
1 |
0 |
1 |
|
|||||
|
|
|
|
|
|
|
|||||
входить три, четыре и так далее |
3 |
0 |
1 |
1 |
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||
минтермов. |
И |
вообще, |
всякая |
4 |
1 |
0 |
0 |
0 |
|
||
|
|
|
|
|
|
|
|
||||
совокупность единиц в колонке |
дает |
5 |
1 |
0 |
1 |
1 |
|
||||
|
|
|
|
|
|
|
|
|
|||
некоторую |
булеву функцию |
и ее |
6 |
1 |
1 |
0 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
||
всегда |
можно |
записать в |
виде |
7 |
1 |
1 |
1 |
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
суммы минтермов.
Если функция представлена в виде сумы минтермов n аргументов, то говорят, что она записана в совершенной дизъюнктивной нормальной форме, сокращенно СДНФ.
Пусть функция, принимающая единичное значение на наборах 001, 010, 100, 101 и 110. Тогда ее аналитическое представление в СДНФ примет вид
 .
.

37
Всякая булева функция заданного числа аргументов представима в виде суммы минтермов единственным образом. По этой причине СДНФ называют
иногда стандартной формой, а также
канонической.
Макстерм (максимальный терм) – это булева функция, которая, в отличие от минтерма, принимает единичное значение на всех наборах, за исключением одного. На этом единственном наборе макстерм принимает нулевое значение. В таблице соответствия для таких функций колонка f содержит точно один нуль и 
№ |
A |
B |
C |
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
1 |
0 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
2 |
0 |
1 |
0 |
1 |
0 |
|
|
|
|
|
|
3 |
0 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
4 |
1 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
5 |
1 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
6 |
1 |
1 |
0 |
1 |
0 |
|
|
|
|
|
|
7 |
1 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
единиц, где n – число аргументов, от которых зависит макстерм.
Макстермы будем обозначать большой буквой M с десятичными индексами по аналогии с обозначением минтермов. Нетрудно заметить, что макстерм – это отрицание минтерма, и наоборот: минтерм – это отрицание макстерма. Воспользуемся этим обстоятельством и найдем аналитическое
выражение макстерма. |
Таблица 4.4 |
||
Пусть функция зависит от аргументов |
|
|
|
, и пусть в таблице соответствия |
|
|
|
в строке 5 колонки |
записан нуль, а во |
|
|
всех остальных строках – единицы (табл. 4.4). |
Добавим справа еще |
одну |
|
колонку и запишем в нее ту же функцию |
, но в инверсной |
форме. |
|
Тогда |
, откуда получаем: |
|
|
 .
.
Индекс макстерма определяется точно так же, как и в случае минтерма.
Макстермом n переменных называется такая их сумма, в которую каждая |
|
переменная входит один раз (с |
отрицанием или без). Очевидно, что число |
различных макстермов такое же, |
как и число минтермов, т.е. , где – число |
переменных макстерма.
Между индексами минтермов и макстермов имеется вполне определенная
связь: |
|
; |
, где |

38
Если задана СДНФ некоторой булевой функции  , то найти ее СКНФ
, то найти ее СКНФ
очень легко. Сначала находим СДНФ инверсии заданной функции. В f войдут все минтермы, отсутствующие в  , и ни один минтерм не войдет одновременно в
, и ни один минтерм не войдет одновременно в  и f . Затем записываем аналитическое выражение для f и результат инвертируем по теореме де Моргана. Проиллюстрируем это примером.
и f . Затем записываем аналитическое выражение для f и результат инвертируем по теореме де Моргана. Проиллюстрируем это примером.
Пусть
 .
.
В эту функцию, зависящую от трех аргументов, не входят минтермы  ,
,  ,
,  . Следовательно, они войдут в инверсию функции
. Следовательно, они войдут в инверсию функции  :
:
.
Инвертируем по теореме де Моргана:
.
Это и есть искомая СКНФ заданной функции  .
.
4.2. Практическая часть
Пример 1. Представить функцию |
|
в совершенной |
дизъюнктивной нормальной форме.
Решение. Составим таблицу истинности для данной функции:
x |
y |
z |
x y |
( x y ) z |
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
|
|
|
|
|
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
1 |
0 |
1 |
0 |
0 |
|
|
|
|
|
1 |
1 |
0 |
1 |
0 |
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
Из таблицы истинности видно, что функция принимает значение 1 на двух наборах 001 и 111. Тогда ее аналитическое представление в СДНФ примет вид
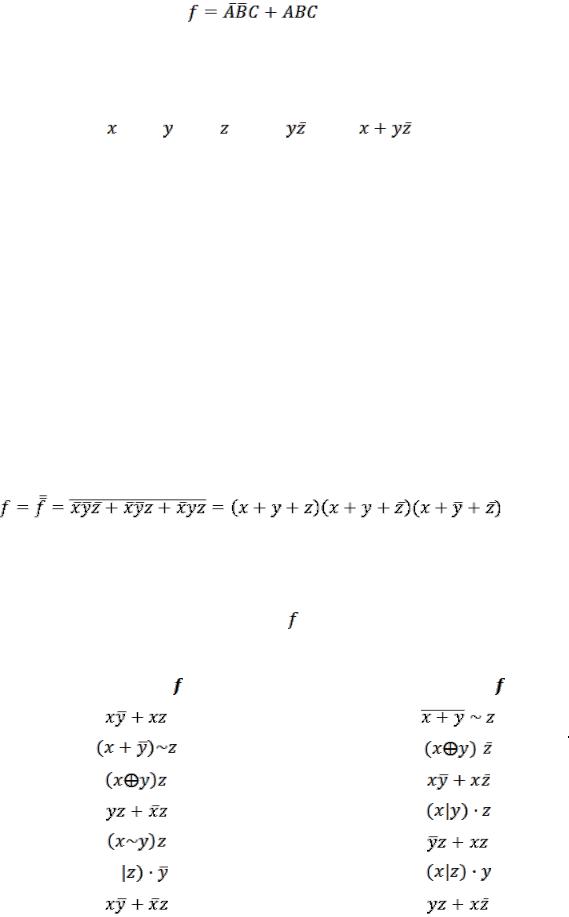
39
Пример 2. Представить функцию  в совершенной конъюнктивной нормальной форме.
в совершенной конъюнктивной нормальной форме.
Решение. Составим таблицу истинности для данной функции:
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
0 |
1 |
0 |
1 |
1 |
|
|
|
|
|
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
1 |
0 |
0 |
0 |
1 |
|
|
|
|
|
1 |
0 |
1 |
0 |
1 |
|
|
|
|
|
1 |
1 |
0 |
1 |
1 |
|
|
|
|
|
1 |
1 |
1 |
0 |
1 |
|
|
|
|
|
Из таблицы истинности видно, что функция принимает значение 0 на трех наборах 000, 001 и 011. Тогда аналитическое выражение для  будет:
будет:
 .
.
Инвертируем по теореме де Моргана:
.
Это и есть искомая СКНФ заданной функции  .
.
4.3. Задачи для самостоятельного решения
Задача 1. |
Представить функцию |
в совершенной дизъюнктивной |
||||
нормальной форме. |
|
|
|
|
||
|
|
|
|
|
|
|
Вариант |
|
Функция |
Вариант |
Функция |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
9 |
· |
|
|
|
|
|
|
|
|
3 |
|
|
|
10 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
11 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
6 |
|
(x |
|
13 |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
14 |
|
|
|
|
|
|
|
|
|

|
|
|
40 |
|
|
|
|
Задача 2. |
Представить функцию |
в совершенной конъюнктивной |
|||||
нормальной форме. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Вариант |
|
Функция |
|
Вариант |
Функция |
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
23 |
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
19 |
|
|
|
|
26 |
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
|
Библиографический список
1.Владимирский, Б. М. Математика. Общий курс [Текст] : учеб. / Б.М. Владимирский, А.Б. Горстко, Я.М. Ерусалимский. – СПб. ; М. ; Краснодар : Лань, 2008. – 960 с.
2.Поздняков, С. Н. Дискретная математика [Текст] : учеб. / С.Н. Поздняков, С.В. Рыбин. – М. : Академия, 2008. – 448 с.
