3992

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежская государственная лесотехническая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

0,24 . Отсюда arccos( 0,24) 104 .

.pdf

Скачиваний:

Добавлен:

08.01.2021

Размер:

738.96 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>


				7x3	10			8x1 80x2 56x3 80

		x1 10x2				8
			17x2 x3		8	1		8x1 17x2		x3 8
		8x1			8	1
		8x1
									63x2 57x3 72
									63x2 57x3 72

	10x2		7x3	10			8x1 80x2 56x3 80

x1					8
		17x2 x3		8	1		8x1 17x2		x3 8
8x1				8	1
8x1
								63x2 57x3		72
								63x2 57x3		72

	10x2		7x3	10			8x1 80x2 56x3 80

x1					8
		17x2 x3		8	1		8x1 17x2		x3 8
8x1				8	1
8x1
								63x2 57x3		72
								63x2 57x3		72

Данное преобразование будем записывать в следующем виде:

x 10x			7x	10	10	8	x 10x 7x				10
x 10x			7x	10	10	8	x 10x 7x				10
	1	2	3					1	2	3
	10x1 9x2 10x3 17				1				91x2 80x3 83
	8x 17x		x	8		1			63x 57x		72
	1	2	3						2	3

Возьмем теперь второе уравнение и с его помощью исключим переменную x2 из третьего уравнения системы. Для этого второе уравнение системы умножим на 63, третье уравнение умножим на 91, и сложим полученные уравнения.

x 10x 7x				10		x 10x 7x 10
x 10x 7x				10		x 10x 7x 10
	1	2	3				1	2	3
		91x2 80x3 83			63			91x2 80x3 83
		63x2 57x3		72	91			147x3 1323
		63x2 57x3		72	91			147x3 1323

Мы привели систему уравнений к так называемому верхнетреугольному виду. Теперь методом обратного хода можно определить

сначала значение переменной			x3 из последнего уравнения системы, затем
значение переменной	x2	из	второго уравнения, и, наконец, значение
переменной x1 из первого уравнения.
x3 9;
91x2 80 ( 9) 83		91x2 637 x2 7;
x1 10 ( 7) 7 ( 9) 10 x1			17.
			13

Ответ: (17, 7, 9) .

б) Решим теперь ту же систему уравнений матричным способом, с

вычислением обратной матрицы.
Как	вычислять определитель det A и как								находить обратную
матрицу A 1 , будет объяснено ниже.
Используя правило умножения (n n) матрицы									и вектор столбца
размера n 1, запишем исходную систему линейных уравнений в виде
AX B,
где
1 10	7			x1			10
A 10 9	10	,		X x	,	B	17	.
				2
	1
8 17	1			x3			8
Поскольку по определению обратной матрицы A 1 имеем
A 1 ( AX ) A 1B EX A 1B ,
и так как EX X , решение системы можно записать в виде
X A 1B .
где A ( 1)i j M			ij	– алгебраические дополнения элементов a матрицы						A
ij			ij						ij

(заметим, что алгебраические дополнения элементов строк записываются в соответствующие столбцы). Получаем:

A		9	10		161 ,		A			10		10	70 ,	A	10			9		98,
11		17		1			12			8		1		13	8			17
		17		1						8		1			8			17
			7								1	7				1		10
A		10	7		129 ,		A				1	7	57 ,	A		1		10	63 ,
21		17		1			22				8	1		23		8		17
		17		1							8	1				8		17
			7						1			7					1	10
A		10	7		163 , A				1			7	80 ,	A			1	10			91.
31		9	10				32		10			10		33			10	9
		9	10						10			10					10	9
Обратная матрица, следовательно, имеет вид
			161			129		163
1	1							80
A				70		57				.
A	147			70		57				.
	147			98		63		91


																		10
Остается умножить матрицу												1
Остается умножить матрицу												A	на столбец B 17									,

																		8

			161		129		163	10		16110 129 17 163 8
		1					80		1	70 10 57 17 80 8
				70		57		17
	147			70		57		17	147
	147			98		63	91		147	98 10 63 17 91 8

								8
	2499				17
1
		1029			7	.
147		1029			7	.
147		1323			9

Результаты совпали.

в) Рассмотрим третий способ решения систем линейных уравнений, который является непосредственным следствием матричной

формулы X A 1B,									правило Крамера.
				Обозначим											через									определитель										матрицы A . Пусть 1 есть
определитель матрицы A , в которой вместо первого столбца стоит столбец B .
Пусть 2 есть определитель матрицы																												A , в которой вместо второго столбца
стоит столбец B . Наконец, пусть 3																										есть определитель матрицы A , в которой
вместо третьего столбца стоит столбец B .
						10	7
	1					10	7
	10					9	10			,
	8					17	1
						10		7										1			10			7					1		10		10
			10			10		7										1			10			7					1		10		10
1			17			9	10					, 2						10			17		10		, 3				10		9		17
			8			17			1									8			8		1						8		17		8
Если 0 ,								то согласно правилу Крамера решение системы уравнений
можно найти по формулам
x		1			,	x		2			,		x			3			.
x		1			,	x		2			,		x						.
1						2							3

Имеем:
						10				7					10					9	10			10			17 10					( 7)			17	9
			10
			10
			17			9			10
1																				17	1						8	1							8	17
			8			17			1											17	1						8	1							8	17
			8			17			1

10 ( 161) 10 ( 63) 7 217 2499;
2				1		10			7					1			17 10					10				10		10		(7)				10 17


				10		17			10
				8		8			1								8				1					8		1						8		8
				8		8			1

1 ( 63) 10 ( 70) 7 ( 56) 1029;

3	1	10	10	1	9	17	10	10	17	10	10	9
	1	10	10
	10	9	17
	8	17	8		17	8		8	8		8	17
	8	17	8

1 ( 217) 10 ( 56) 10 98 1323.

Следовательно, по формулам Крамера,

x 2499		17 ,	x	1029	7 ,	x	1323	9 .
1	147		2	147		3	147
	147			147			147

Ответы вновь совпали.

Пример 2. Решить систему уравнений

3x1 10x2	7x3	x4	3;
4x1 17x2	15x3	9x4	33;

23x1 16x2	5x3 13x4		51.

Решение. С помощью первого уравнения исключим переменную x1 из второго и третьего уравнений системы.

	3x1 10x2 7x3		x4		3;	4	23
	3x1 10x2 7x3		x4		3;	4	23
	4x1 17x2 15x3		9x4		33;
	4x1 17x2 15x3		9x4		33;	3
	23x1 16x2 5x3 13x4				51.		3
	23x1 16x2 5x3 13x4				51.		3
Получаем:
3x1 10x2 7x3			x4	3;
	91x2 73x3	31x4		111;
	91x2 73x3	31x4		111;
	182x2 146x3	62x4		222.
	182x2 146x3	62x4		222.

Исключим теперь с помощью второго уравнения системы переменную x2 из третьего уравнения.

3x1 10x2 7x3		x4	3;

	91x2 73x3	31x4	111;
				2
	182x2 146x3	62x4	222.	1

В результате третье уравнение системы превращается в тождеств 0 = 0, и остается только два уравнения:

3x1 10x2 7x3		x4 3;
	91x2 73x3	31x4 111.

		16

Мы привели систему к верхнетреугольному виду, однако для двух неизвестных (а именно, для x3 и для x4 ) не хватило ―своего‖ уравнения для преобразования исключения. В этом случае переменные x3 , x4 объявляются свободными (то есть их значения могут выбираться произвольным образом), а значения остальных переменных (они называются базисными) могут быть выражены через значения свободных переменных.

x3 t,

x4 s,

3x1 10x2 7t s 3; 91x2 73t 31s 111.

Отсюда:


x			111				73		t					31			s,
x									t								s,
2	91				91							91
	91				91							91
x		10		x 1							7		t					1	s			10		(	111		73		t		31		s) 1	7	t	1	s
x				x 1									t						s					(					t				s) 1		t		s
1	3				2					3		3								3			91			91				91				3		3
	3									3		3								3			91			91				91				3		3
	279				31			t		73					s.
								t							s.
	91				91					91
Ответ:					(	279							31			t				73	s,		111			73		t		31		s,t, s) ,		где		t, s R
Ответ:					(											t					s,							t				s,t, s) ,		где		t, s R
					91							91								91			91			91				91

произвольные параметры.

2.2ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

1.Решить систему линейных уравнений тремя способами:

а) методом Гаусса последовательных исключений неизвестных; б) по формуле x A 1b с вычислением обратной матрицы A 1 ; в) по формулам Крамера.

x1 mx2 nx3 m;

mx1 (m 1)x2 mx3 m n;

(n 1)x1 (m n)x2 x3 n 1.

1. Решить методом Гаусса следующую вырожденную систему уравнений

(n m)x1 mx2 nx3 x4 m n;

(2n m)x1 (m n)x2 (2n 1)x3 (2 n)x4 4m n;(n 3m)x1 (3m 2n)x2 (n 2)x3 (1- 2n)x4 3m 3n.

Значения параметров m и n, выбирается в соответствии с двумя последними цифрами зачетной книжки A и B.

Каждая задача зависит от двух числовых параметров m и n, которые определяются по цифрам A и B из таблиц:

А	0	1	2	3	4	5	6	7	8	9

m	2	6	4	8	8	2	6	4	4	6


B	0	1	2	3	4	5	6	7	8	9

n	3	5	1	7	9	1	3	7	5	9

							3. ВЕКТОРНАЯ АЛГЕБРА
							3.1 ПРАКТИЧЕСКАЯ ЧАСТЬ
Пример			1. Найти			векторное			произведение				a b , если	a 3i j 2k ,
b 2i 3 j 5k .
Решение. По формуле (2.1) получаем
	i	j	k		1	2		3	2		3 1


a b	3	1	2	i			j			k
	2	3	5		3 5			2	5		2 3	.
	2	3	5

5 6 i 15 4 j 9 2 k i 11 j 7k

Пример 2. Вычислить площадь треугольника с вершинами А(7, 3, 4), В(1, 0, 6), С(4, 5, –2).

Решение. По формуле (2.3) имеем S 12 AB AC .

1) Найдем координаты векторов AB и AC . Для этого вычтем из координат конца вектора координаты начала

AB xB xA,		yB yA,			zB zA 1 7,				0 3,		6 4 6,		3,	2
AC xC xA,		yC yA,			zC zA 4 7,				5 3,		2 4 3, 2,			6
2) Найдем векторное произведение
	i	j	k			3 2		6	2		6	3


AB AC	6	3	2	i			j			k
	3	2	6			2 6		3	6		3	2
	3	2	6

18 4 i 36 6 j 12 9 k 14i 42 j 21k

3) AB AC 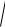142 42 2 21 2 74 36 9 49

S ABC

AB AC

49 24,5кв.ед.

Пример

3. Сила F 2i 3 j 4k приложена к точке А(3, 4, –2). Найти ее

момент М относительно точки О(4, 2, –1).

Решение. Находим вектор OA i 2 j k .

Искомый момент M равен векторному произведению OA F

M OA F

2 1

5i 2 j k .

Пример

4. Пирамида ABCD

задана

координатами вершин. Пользуясь

понятиями и формулами векторной алгебры, найти:

1)длину ребра AB;

2)угол между ребрами AB и AD ;

3)площадь грани ABC ;

4)объем пирамиды.

A(6;6;2) ,

B(5;4;7) ,

C(2;4;7) , D(7;3;0) .

Решение.

Координаты

вектора

ax i ay

j az

k находятся по

формулам: ax

x1 x0 , ay y1 y0 ,

az z1 z0 ,

где (x0 ; y0 ; z0 ) – координаты начала,

(x1; y1; z1 ) –

координаты конца

вектора

a. Тогда

длина

вектора a

равна

a2 .

Рис. 2.22.

Рассмотрим вектор AB . Точка A(6;6;2)

является началом, а точка B(5;4;7) –

концом вектора AB . Следовательно, вектор AB имеет следующие координаты:

AB {5 6; 4 6; 7 2} { 1; 2; 5}, а значит

( 1)2 ( 2)2 52 1 4 25 30 .

Косинус угла

между векторами a и b может быть найден по формуле:

cos

где a

ax bx ay by az bz – скалярное произведение векторов

a и b .

Для того,

чтобы найти угол между ребрами AB и AD ,

введем в рассмотрение

векторы

AB и

AD.

Так как координаты

вектора AB и

его длина известны,

определим координаты и длину вектора AD :

AD {7 6; 3 6; 0 2} {1; 3; 2},

AD 12 ( 3)2 ( 2)2 1 9 4 14 .

Тогда

cos	AB AD		( 1) 1 ( 2) ( 3)		5 ( 2)	5

	AB	AD		30 14		30 14
	AB	AD		30 14		30 14
					20
					20

3)Площадь треугольника, построенного на векторах a и b , находится по

формуле S

, через векторное произведение

(aybz azby ) i

(axbz azbx ) j (axby

aybx ) k .

Площадь

грани

ABC есть

площадь

треугольника

ABC ,

построенного на

векторах AB и AC . Так как AC { 4; 2; 5}, тогда

AB AC

( 10 10) i ( 5

20) j (2

0 i

15 j

6k ,

а значит

S ABC 12 AB AC 12 02 ( 15)2 ( 6)2 12 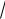225 36 12 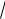261

	1			3
	1		9 29	3		29 8,1.
			9 29			29 8,1.
	2	2
		4) Объем			V треугольной
		4) Объем			V треугольной					пирамиды, построенной на векторах a ,		b ,	c
							1
							1
находится по формуле V								(a	b) c		.
находится по формуле V							6	(a	b) c		.
							6

	1
В нашем случае V		( AB AC) AD	.
	6


Так как AB AC {0; 15; 6}, AD {1; 3; 2}, получаем:

V	1	0 1 ( 15) ( 3) ( 6) ( 2)	1	57	57	9,5 .

	6		6		6

3.2 ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

Задача. Пирамида ABCD задана координатами вершин. Пользуясь понятиями

иформулами векторной алгебры, найти:

1)длину ребра AB ;

2)угол между ребрами AB и AD ;

3)площадь грани ABC ;

4)объем пирамиды.

Вариант 0.	A(7;5;3) , B(9;4;4) , C(4;5;7) , D(7;9;6) .
Вариант 1.	A(6;1;1) , B(4;6;6) , C(4;2;0) , D(1;2;6) .
Вариант 2.	A(5;5;4) , B(3;8;4) , C(3;5;10) , D(5;8;2) .
Вариант 3.	A(0;7;1) , B(4;1;5) , C(4;6;3) , D(3;9;8) .
Вариант 4.	A(9;5;5) , B( 3;7;1) , C(5;7;8) , D(6;9;2) .
Вариант 5.	A(2;4;3) , B(7;6;3) , C(4;9;3) , D(3;6;7) .
Вариант 6.	A(3;5;4) , B(5;8;3) , C(1;9;9) , D(6;4;8) .
Вариант 7.	A(3;3;9) , B(6;9;1) , C(1;7;3) , D(8;5;8) .
Вариант 8.	A(3;1;4) , B( 1;6;1) , C( 1;1;6) , D(0;4; 1) .
Вариант 9.	A(6;6;7) , B(5;7;8) , C(2;2;2) , D(2;5;4) .

4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

4.1 ПРАКТИЧЕСКАЯ ЧАСТЬ

Пример 4.1. Составить уравнение прямой, проходящей через точку 3;4 и

наклоненной к оси Ox под углом 135o .

Решение. Уравнение прямой можно записать в форме (4.7). Здесь x0 3,

	y	0	4 ,		k tg135o 1.
		0
				Следовательно, искомое уравнение будет
									y 4 1 x 3 или					y x 1.
				Пример 4.2. Составить уравнение прямой линии, проходящей через точки
	A 1;2 и B 1;1 .
				Решение. Подставляя в уравнение (4.9) x0 1,											y0 2 ,	x1 1,	y1 1, получим
	y 2				x 1	, откуда		y 2				x 1	или 2 y 4 x 1
	1 2					, откуда		1					или 2 y 4 x 1
	1 2				1 1			1				2
или окончательно y								1	x	3	.
или окончательно y							2		x	2	.
							2			2

Пример 4.3. Найти угол между прямыми y 2x 3 и 3x y 2 0 .

Решение. Если перенумеровать прямые в том порядке, как они заданы, то угловой коэффициент первой прямой будет k1 2 , а для второй прямой k2 3. Тогда по формуле (4.11) получим

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.01.2021735.8 Кб23988.pdf
#
08.01.2021736.37 Кб23989.pdf
#
08.01.2021194.53 Кб2399.pdf
#
08.01.2021737.66 Кб13990.pdf
#
08.01.2021737.75 Кб33991.pdf
#
08.01.2021738.96 Кб13992.pdf
#
08.01.2021739.02 Кб13993.pdf
#
08.01.2021739.14 Кб123994.pdf
#
08.01.2021739.57 Кб23995.pdf
#
08.01.2021741.13 Кб93996.pdf
#
08.01.2021742.39 Кб13998.pdf