
3992
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ИМЕНИ Г.Ф. МОРОЗОВА»
МАТЕМАТИКА ЛИНЕЙНАЯ АЛГЕБРА
Методические указания к практическим занятиям
для студентов по специальности
09.05.01 – Применение и эксплуатация автоматизированных систем специального назначения (специализация «Автоматизированные системы обработки информации и управления»)
Воронеж 2017
3
УДК 512.8
Сапронов , И. В. Математика. Линейная алгебра [Текст] : методические указания к практическим занятиям для студентов по специальности 09.05.01 – Применение и эксплуатация автоматизированных систем специального назначения (специализация «Автоматизированные системы обработки информации и управления») / И.В. Сапронов , Н.М. Спирина , Е. В. Раецкая; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2017. – 34 с.
Печатается по решению учебно-методического совета
ФГБОУ ВО «ВГЛТУ» (протокол № |
от 2017 г.) |
Рецензент д-р физ.-мат. наук, доцента кафедры математического анализа ВГУ Зубова С.П.
4
Содержание Введение……………………………………………………………………………..4
1.Матрицы и определители……………………………………………………….5
1.1Практическая часть……………………………………………………………5
1.2Индивидуальные задания……………………………………………………..7
2.Системы линейных уравнений……………………………………………...….9
2.1Практическая часть……………………………………………………………9
2.2Индивидуальные задания……………………………………………………15
3.Векторная алгебра……………………………………………………………..16 3.1 Практическая часть………………………………………………….……….16
3.2 Индивидуальные задания…………………………………………………. ..19
4.Аналитическая геометрия…………………………………………………….20
4.1 Практическая часть…………………………………………………………..20
4.2 Индивидуальные задания…………………………………………………. ..25
5.Кривые второго порядка……………………………………………………..26 5.1 Практическая часть…………………………………………………………..26 5.2 Индивидуальные задания…………………………………………………. ..29
Вопросы для контроля. ………………………………………………………….31
Библиографический список ……………………………………………………34
5
ВВЕДЕНИЕ
Целью изучения дисциплины «Линейная алгебра» является воспитание достаточно высокой математической культуры, привитие навыков современных видов математического мышления, обучение основным математическим понятиям и методам линейной алгебры, необходимым для анализа и моделирования устройств, процессов и явлений при поиске оптимальных решений практических задач, методам обработки и анализа результатов численных экспериментов для экономических задач.
Основной задачей является выработка умения решать примеры и задачи для последующего применения математических методов в различных приложениях.
Студент по результатам освоения дисциплины «Линейная алгебра» должен обладать способностью выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы.
Врезультате освоения дисциплины студент должен:
-знать основные понятия, определения и методы исследования объектов с помощью теорем и формул различных разделов курса математики;
-уметь: решать задачи и примеры по различным разделам высшей математики
сдоведением решения до практического приемлемого результата (формулы, числа, графика, качественного вывода и т.п.),
- уметь при решении задач выбирать необходимые вычислительные методы и средства (ПЭВМ, таблицы и справочники);
-самостоятельно изучать научную литературу по математике;
- иметь представление о численных алгоритмах решения математических и прикладных задач его профессиональной области.
6
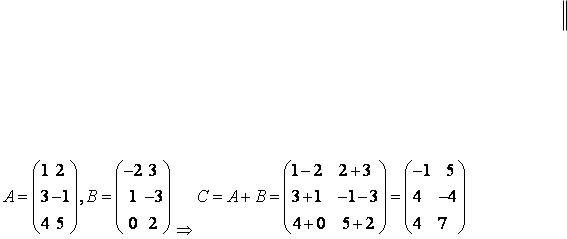
|
1. |
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ |
|
|
|
1.1 ПРАКТИЧЕСКАЯ ЧАСТЬ |
|
Матрицей А размера m n называется таблица из |
m n чисел |
||
a |
a ... |
a |
|
11 |
12 |
1n |
|
a21 |
a22 ... |
a2n |
|
A |
|
... |
|
... ... ... |
|
||
|
|
|
|
|
am2 ... |
|
|
am1 |
amn |
|
|
Часто для краткости пишу A 
 aij
aij 
 . Числа, из которых состоит
. Числа, из которых состоит
матрица, называются элементами матрицы. Индексы у элементов матрицы указывают расположение этого элемента в таблице: первый индекс – номер строки, в которой находится элемент, а второй – номер столбца. Например, элемент a21 находится на пересечении второй строки и первого столбца:
|
a |
a |
... |
a |
|
|
|
|
11 |
12 |
|
1n |
|
|
|
|
|
|
||
|
a21 |
a22 |
... |
a2n |
||
A |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
||
... |
... |
... |
... |
|
||
|
|
am2 |
... |
|
|
|
am1 |
amn |
|||||
Суммой двух матриц одинакового размера m n |
A |
|
aij |
|
и B |
|
bij |
||||
называют матрицу C |
|
|
размера m n такую, что |
|
|
|
|
|
|
|
|
|
cij |
|
|
|
|
|
|
|
|
||
cij aij bij , |
i 1,..., m ; j 1,...n . |
|
|
|
|
|
|
|
|||
.
7
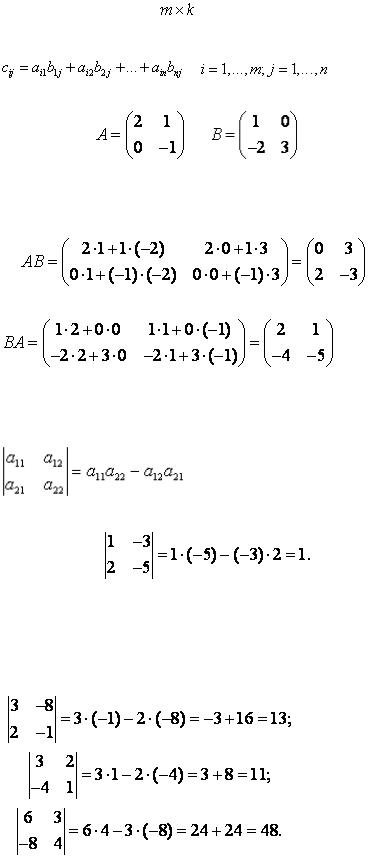
Произведением матриц АВ называется матрица
C |
|
cij |
|
размера |
, у которой |
|
|
|
|
|
, |
Пусть,
Тогда
,
.
Определителем матрицы 2-го порядка называется число
.
Например,
Найдем определители 
Определителем матрицы 3-го порядка называется число
8
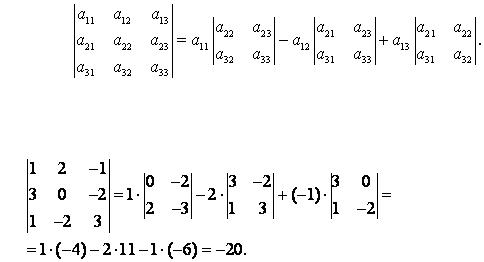
например,
1.2 ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
Вариант 2.
Вариант 3.
Задача 1.
Для матриц А и B вычислить
a)2A 4B
b)A (B A)
c)A2 B A A
|
|
3 |
0 |
4 |
|
|
Вариант 0. |
|
2 |
2 |
|
|
, |
A |
3 |
|||||
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|||
|
|
1 |
0 |
1 |
|
|
Вариант 1. |
|
2 |
1 |
2 |
|
, |
A |
|
|||||
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|||
|
4 |
1 |
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
A |
2 |
0 2 |
|
, |
B 1 |
|||
|
3 |
1 |
|
2 |
|
|
|
|
|
|
|
|
1 |
||||
|
0 |
1 |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
A |
3 |
1 |
2 |
|
, |
|
B |
2 |
|
3 |
3 |
2 |
|
|
|
|
3 |
|
|
|
|
|
||||
|
|
|
1 |
|
B |
|
0 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
7 |
|
B |
|
5 |
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
3 |
|
|
2 |
4 . |
|
|
2 |
|
|
|
4 |
|
|
|
3 |
0 |
|
|
2 |
4 . |
|
|
1 |
|
|
|
1 |
|
|
|
1 |
2 |
|
1 |
2 . |
|
3 |
1 |
|
|
||
1 |
3 |
|
1 |
2 |
. |
1 |
4 |
|
|
||
|
3 |
1 |
0 |
|
1 0 |
2 |
||||
Вариант 4. |
|
2 |
1 |
|
, |
|
3 |
1 |
2 |
|
A |
3 |
B |
. |
|||||||
|
|
5 |
1 |
|
|
|
5 |
4 |
1 |
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
4 |
0 2 |
|
|
|
1 |
|
1 2 |
|
|
|
|
|
|
|
|||||||||||||||
Вариант 5. |
A |
|
1 |
1 |
|
|
|
|
|
, |
B |
|
0 |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
3 |
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
5 |
1 2 |
|
|
|
|
|
5 |
|
5 |
|
0 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
5 4 |
|
|
5 |
|
1 2 |
|
|
|
|
|
|
|
|
|||||||||||||||
Вариант 6. |
A |
|
2 |
2 |
|
|
4 |
|
, |
B |
|
|
0 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1 . |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
1 |
1 |
|
|
2 |
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
0 |
|
|
4 |
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вариант 7. |
A |
|
2 |
2 |
|
|
3 |
|
, |
|
B |
|
3 |
5 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
3 |
7 |
2 |
|
|
|
|
|
5 3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
3 |
1 |
4 |
|
|
|
|
1 |
|
1 2 |
|
|
|
|
|
|
|
|||||||||||||
Вариант 8. |
A |
|
3 |
2 |
|
|
0 |
|
, |
|
B |
|
|
|
0 |
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
4 |
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
1 |
1 2 |
|
|
|
|
|
|
2 |
|
4 |
|
3 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 |
0 4 |
|
3 1 |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Вариант 9. |
|
|
2 |
3 |
1 |
|
, |
|
0 |
6 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
A |
|
B |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
1 |
1 5 |
|
|
|
2 3 |
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Задача 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Вычислить определители |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
а) второго порядка; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
б) третьего порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Вариант 0. |
а) |
|
|
|
, |
|
|
|
|
|
|
|
|
|
б) |
|
|
|
3 |
4 |
2 |
. |
||||||||||
|
|
|
4 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 |
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Вариант 1. |
а) |
, |
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
3 |
1 |
5 |
|
. |
|||||||||||
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
3 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
5 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Вариант 2. |
а) |
|
|
, |
|
|
|
|
|
|
|
|
|
б) |
|
|
3 |
4 |
2 |
|
. |
|||||||||||
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
1 |
2 |
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вариант 3. а) |
|
5 |
3 |
|
, |
|
|
||||
|
|
7 |
2 |
|
|
|
|
|
|
|
|
Вариант 4. а) |
|
2 |
3 |
|
, |
|
|
||||
|
6 |
1 |
|
Вариант 5. а) |
|
6 |
|
, |
2 |
|
|||
4 |
3 |
|
||
|
|
|
|
|
Вариант 6. а) |
|
8 |
|
, |
5 |
|
|||
2 |
3 |
|
Вариант 7. а) |
|
3 |
|
, |
8 |
|
|||
4 |
2 |
|
||
|
|
|
|
|
Вариант 9. а) |
|
4 |
|
, |
|||
6 |
|
||||||
3 |
2 |
|
|||||
Вариант 9. а) |
|
5 |
6 |
|
, |
|
|
|
|
|
|
||||
|
2 |
3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
||
|
|
3 |
|
||||||||||
б) |
4 |
3 |
2 |
|
|
. |
|||||||
|
|
1 |
4 |
3 |
|
|
|
|
|
|
|||
|
|
|
|
2 |
3 |
|
|
|
|||||
|
|
|
3 |
|
|
||||||||
б) |
|
1 |
2 |
3 |
|
|
. |
||||||
|
|
|
2 |
1 |
1 |
|
|
|
|||||
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
б) |
|
2 |
1 |
3 |
. |
||||||||
|
|
|
1 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|||||
|
|
|
2 |
|
|
||||||||
б) |
|
1 |
1 |
2 |
|
|
|
. |
|||||
|
|
|
3 |
2 |
2 |
|
|
|
|||||
|
|
|
3 |
2 |
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
||||||
б) |
|
3 |
2 |
2 |
|
. |
|||||||
|
|
|
1 |
3 |
2 |
|
|
||||||
|
|
|
3 |
2 |
|
|
|||||||
|
|
|
2 |
|
|||||||||
б) |
|
3 |
1 |
2 |
|
. |
|||||||
|
|
|
1 |
2 |
1 |
|
|
||||||
|
|
3 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
б) |
|
1 |
3 |
2 |
. |
||||||||
|
|
2 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
2.1ПРАКТИЧЕСКАЯ ЧАСТЬ
Пример 1. Решить систему трех уравнений с тремя неизвестными:
11

x |
10x 7x |
10; |
||
1 |
|
2 |
3 |
|
10x1 9x2 |
10x3 17; |
|||
8x |
17x |
x |
8. |
|
|
1 |
2 |
3 |
|
Найдем решение:
а) методом Гаусса последовательных исключений неизвестных; б) по формуле x A 1b с вычислением обратной матрицы A 1 ; в) по формулам Крамера.
Решение. а) Начнем с метода Гаусса последовательных исключений неизвестных. Сначала нужно преобразовать систему уравнений так, чтобы переменная x1 осталась только в одном уравнении системы, например, в первом. Затем уравнение, в которое входит x1 , отбрасывают, и рассматривают систему из оставшихся уравнений, в котором число уравнений и число неизвестных уменьшилось. Эту редуцированную систему преобразуют так, чтобы переменная x2 осталась только в одном уравнении. Затем уравнение, в которое входит x2 , отбрасывают, и вновь рассматривают систему из меньшего числа уравнений. Преобразования с последовательным исключением неизвестных x1 , x2 , x3 и т.д. продолжают до тех пор, пока к каждой неизвестной не будет применена процедура исключения. После этого значения x1 , x2 , x3 ,… определяют сначала из последнего уравнения, затем из предпоследнего и т.д., вплоть до первого уравнения.
Итак, возьмем первое уравнение системы и с его помощью исключим переменную x1 из второго и третьего уравнений. Для этого первое уравнение перепишем без изменений, а второе и третье уравнения сложим с подходящими коэффициентами с первым уравнений системы. Сначала умножим первое уравнение системы на 10, второе на 1, а затем сложим полученные уравнения. Получим
|
|
|
|
|
|
|
|
|
|
x1 |
10x2 7x3 |
10 |
|
|
10x1 100x2 70x3 |
100 |
|
|
|
|||||||
|
10 |
|
||||||
|
|
9x2 10x3 |
17 |
1 |
10x1 |
9x2 10x3 |
17 |
|
10x1 |
|
|||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
91x2 80x3 |
83 |
|
|
|
|
|
|
|
||
Аналогично, умножим первое уравнение системы на 8, второе на 1, а затем сложим.
12
