
3888
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный лесотехнический университет имени Г.Ф. Морозова»
ЭКОНОМЕТРИКА
Методические указания к практическим занятиям для студентов по направлению подготовки 38.03.01 – Экономика
Воронеж 2016
2
УДК 330.43:519.2 ББК 65в631
Писарева, С. В. Эконометрика [Текст]: м етодические указания к практическим занятиям для студентов по направлению подготовки 38.03.01 – Экономика / С.В.Писарева; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2016. – 39 с.
Печатается по решению учебно-методического совета ФГБОУ ВО «ВГЛТУ» (протокол № 3 от 29.01.2016 г.)
Рецензент доктор физ.-мат. наук, профессор, заведующий кафедрой математического моделирования ФГБОУ ВО «Воронежский государственный университет» В.А. Костин
3
Оглавление |
|
Введение |
4 |
Практическая работа №1. Построение и анализ линейной модели парной |
5 |
регрессии |
|
Практическая работа № 2. Построение и анализ нелинейной модели |
10 |
парной регрессии |
|
Практическая работа № 3. Построение линейной модели множественной |
15 |
регрессии |
|
Практическая работа № 4. Проверка существенности факторов и |
20 |
показатели качества уравнения множественной регрессии |
|
Практическая работа № 5. Анализ автокорреляции уровней временных |
23 |
рядов |
|
Практическая работа № 6. Анализ аддитивных и мультипликативных |
27 |
моделей временных рядов |
|
Приложение 1. |
35 |
Приложение 2. |
37 |
Библиографический список |
38 |
4
Введение
Развитие экономики, усложнение экономических процессов и повышение требований к принимаемым управленческим решениям в области макро- и микроэкономики потребовало более тщательного и объективного анализа реально протекающих процессов на основе привлечения современных математических и статистических методов.
С другой стороны, проблема нарушения предпосылок классических статистических методов при решении реальных экономических задач привели к необходимости развития и совершенствования классических методов математической статистики и уточнения постановок соответствующих задач.
В результате этих процессов осуществилось выделение и формирование новой отрасти знания под названием «эконометрика», связанной с разработкой и применением методов количественной оценки экономических явлений, процессов и их взаимосвязей.
Методические указания состоят из шести практических работ, в результате выполнения которых, пользователь должен освоить умения и навыки построения парной и множественной регрессии, анализу их факторов и показателей, анализу моделей временных рядов.
Каждая практическая работа содержит необходимые теоретические сведения, задания к работе, порядок выполнения работы, варианты исходных данных для построения и анализа эконометрических моделей.
Данные методические указания к выполнению практических работ по дисциплине «Эконометрика» предназначены для бакалавров по направлению подготовки 38.03.01 – «Экономика», целью преподавания которой является формирование у студентов способности к количественному анализу реальных экономических явлений.
.
5
Практическая работа № 1 ПОСТРОЕНИЕ И АНАЛИЗ ЛИНЕЙНОЙ МОДЕЛИ
ПАРНОЙ РЕГРЕССИИ
Цель работы: на основе исходных данных построить и провести анализ линейной модели парной регрессии.
Теоретическая часть
Линейная модель парной регрессии представляет собой уравнение вида
yx a b x, |
(1.1) |
где yx – зависимая переменная (результативный признак); x – независимая переменная (признак фактор).
Данное уравнение позволяет по заданным значениям фактора x находить теоретические значения результативного признака yx , подставляя в него фактические значения фактора x .
Построение линейной регрессии сводиться к оценке ее параметров – a и b . Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Согласно данному методу параметры a и b находятся из решения системы линейных уравнений
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|
||||||||
|
|
|
|
|
|
|
a n b xi yi ; |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
i 1 |
i 1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
n |
|
|
n |
|
n |
|
|
|
(1.2) |
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
b xi |
xi yi |
|
|
|
|
|||||||||||
|
|
|
|
|
|
a xi |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
i 1 |
|
i 1 |
|
i 1 |
|
|
|
|
|||||||||
где n – число наблюдений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Решая систему уравнений (1.2) относительно параметров a и b получим |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
b |
|
|
|
|
, |
|
|
|
|
|||||||
|
|
|
|
a y b x, |
|
|
x y |
y x |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.3) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 x 2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
n |
|
1 |
n |
|
|
|
|
1 |
|
|
n |
|
|
|
|
|
1 |
n |
|
||
где |
x |
xi , |
y |
yi , |
x y |
|
yi xi , x2 |
|
xi |
2 . |
||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
n i 1 |
|
n i 1 |
|
|
|
|
n i 1 |
|
|
|
|
|
n i 1 |
|
||||||||

6
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает
линейный |
коэффициент |
корреляции |
rxy , |
который |
можно |
рассчитать по |
||||||||||||||||||||
формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
b |
x , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
xy |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
(1.4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где x |
|
|
(xi |
x)2 |
|
|
x2 x 2 ; |
y |
|
|
( yi |
y)2 |
|
|
|
y2 y 2 . |
||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
n i 1 |
|
|
|
|
|
|
|
|
|
|
|
n i 1 |
|
|
|
|
|
|
|
|
|||
Линейный |
коэффициент |
корреляции |
находиться |
в |
пределах: |
|||||||||||||||||||||
1 rxy |
1. Чем ближе абсолютное значение |
rxy |
к единице, тем сильнее |
|||||||||||||||||||||||
линейная |
|
|
связь |
между |
факторами |
(при |
rxy 1 |
имеем |
строгую |
|||||||||||||||||
функциональную зависимость), чем ближе к нулю, тем линейная связь слабее.
|
|
Для оценки качества подбора линейной функции рассчитывается квадрат |
||||||||||||||
линейного коэффициента корреляции |
|
|
rxy |
2 |
, называемый |
коэффициентом |
||||||||||
детерминации |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
1 |
ост |
|
|
|
|
|
|
||||||
|
|
|
|
rxy |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
|
|
|
(1.5) |
|||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|||
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ост2 |
( yi yx )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для качества модели по относительным отклонениям по каждому |
||||||||||||||
наблюдению, определяют ошибку аппроксимации |
|
|
|
|||||||||||||
|
|
|
|
|
|
yi yxi |
|
|
|
|
||||||
|
|
|
|
Ai |
|
|
100%. |
|
(1.6) |
|||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
yi |
|
|
|
|
|
|
|
|
|
|
|
|
Оценка значимости уравнения регрессии в целом производиться на |
||||||||||||||
основе F-критерия Фишера. Значение F-критерия для линейной модели |
||||||||||||||||
регрессии может быть определено через коэффициент детерминации rxy |
2 |
по |
||||||||||||||
следующей формуле
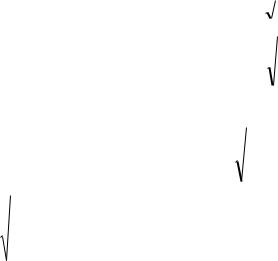
7
|
|
|
r 2 |
|
|
|
F |
|
xy |
(n 2). |
|
|
1 r 2 |
(1.7) |
|||
|
|
|
xy |
|
|
Фактическое значение F-критерия Фишера (1.7) сравнивается с |
|||||
табличным значением Fтабл( , k1, k2 ) при уровне значимости a |
и степенях |
||||
свободы k1 m и k2 |
n m 1, |
где m – число независимых переменных в |
|||
уравнении регрессии |
(в случае |
парной |
регрессии m 1 ). При |
этом, если |
|
фактическое значение F-критерия больше табличного, то признается статистическая значимость уравнения в целом.
В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому
из параметров определяется его стандартная ошибка: mb и ma . Кроме того стандартная ошибка определяется для линейного коэффициента корреляции mr .
Стандартные ошибки определяется из соответствующих выражений
|
|
|
|
|
|
mb |
|
Sост |
|
|
|
; |
|
|
|
|
|
(1.8) |
|||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Sост |
|
|
xi |
2 |
|
|
|
||||||||
|
|
|
|
|
|
ma |
|
|
|
|
|
|
|
i 1 |
|
|
; |
(1.9) |
|||||
|
|
|
|
|
|
|
|
|
x n |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 r |
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
xy |
|
, |
|
|
|
(1.10) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
r |
|
|
|
|
n |
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( yi yx )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Sост |
|
i 1 |
|
|
- корень несмещенной оценки остаточной дисперсии. |
||||||||||||||||||
n |
2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Фактические значения t-критерия Стьюдента для параметров a , b и
линейного коэффициента корреляции rxy определяются из выражений
tb |
b |
, ta |
|
a |
, tr |
|
rxy |
. |
|
mb |
ma |
mr |
(1.11) |
||||||
|
|
|
|
|
|
|
Далее фактические значения t-критериев сравниваются с табличным значением при определенном уровне значимости и числе степеней свободы
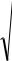
8
n 2 . Если фактическое значение t-критерия больше табличного, то признается статистическая значимость данного параметра уравнения регрессии. Доверительные интервалы для параметров регрессии a и b определяются как
a tтаблma и b tтаблmb .
В прогнозных расчетах по уравнению регрессии определяется предсказываемое yпр значение как точный прогноз xпр x , т.е. путем подстановки в уравнение регрессии yx a b x соответствующего значения x . Поэтому он дополняется расчетом стандартной ошибки прогнозируемого индивидуального значения yпр
|
1 |
|
(xпр x)2 |
|
|
||
myп р Sост |
1 |
|
|
|
|
(1.12) |
|
n |
n x |
2 |
|||||
и, соответственно, интервальной оценкой прогнозируемого индивидуального значения yпр
|
|
|
yпр |
y |
пр |
yпр yпр y |
, |
(1.13) |
|
|
|
|
|
|
пр |
|
|
где y |
пр |
my |
tтабл . |
|
|
|
|
|
|
|
пр |
|
|
|
|
|
Практическая часть
Задание к работе
1.На основе исходных данных (см. таб. 1.1), где N – номер варианта, соответствующий трем последним цифрам номера зачетной книжки, построить
ипровести анализ линейной модели парной регрессии.
2.Выписать пояснения к каждому выполненному пункту задания.
3.Сделать итоговый вывод об обоснованных результатах, полученных в ходе выполнения работы.
9
|
|
Таблица 1.1 |
Исходные данные для лабораторных работ №1 и №2 |
||
|
|
|
Номер измерения |
x |
y |
|
|
|
1 |
1,2 N |
0,9 N |
|
|
|
2 |
3,2 N |
1,2 N |
|
|
|
3 |
5,3 N |
1,8 N |
|
|
|
4 |
7,4 N |
2,2 N |
|
|
|
5 |
9,6 N |
2,6 N |
|
|
|
6 |
11,8 N |
2,9 N |
|
|
|
7 |
14,5 N |
3,3 N |
|
|
|
8 |
18,7 N |
3,8 N |
|
|
|
9 |
20,8 N |
4,1 N |
|
|
|
10 |
24,1 N |
4,4 N |
|
|
|
|
D, %= 100+N |
|
|
|
|
Порядок выполнения работы
1. Для удобства проводимых в ходе выполнения работы вычислений составить таблицу 1.2 на основе исходных данных к работе (столбцы 7, 8, 9 заполняются после выполнения п. 2 данного порядка, столбец 10 – после выполнения п. 3).
Таблица 1.2
№ |
x |
y |
x y |
x 2 |
y 2 |
yx |
y yx |
y y |
x |
2 |
Ai. ,% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сумма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Среднее |
|
|
|
|
|
|
|
|
|
|
|
значение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2.Построить линейное уравнение парной регрессии yx от x вида
(1.1), найдя его параметры a и b из выражений (1.3).
3. Рассчитать линейный коэффициент парной корреляции (1.4), коэффициент детерминации (1.5) и ошибку аппроксимации (1.6).
10
4.Оценить статистическую значимость уравнения регрессии в целом на основе F-критерия Фишера. Необходимо рассчитать фактическое значение F-критерия (1.7) и сравнить его с табличным значением (см. прил. 1).
5.Оценить статистическую значимость параметров уравнения регрессии и линейного коэффициента корреляции на основе t-критерия
Стьюдента. Необходимо рассчитать фактические значения t-критерия для a , b
и rxy с помощью выражений (1.11) и сравнить их с табличным значением (см. прил. 2). Далее рассчитать доверительные интервалы параметров регрессии a и b .
6.Выполнить прогноз yпр при прогнозном значении xпр ,
составляющем D% от среднего уровня x . Оценить точность прогноза, рассчитав ошибку прогноза (1.12) и его доверительный интервал (1.13).
7.На одном графике построить исходные данные (зависимость y от x)
итеоретическую прямую.
Практическая работа № 2 ПОСТРОЕНИЕ И АНАЛИЗ НЕЛИНЕЙНОЙ МОДЕЛИ
ПАРНОЙ РЕГРЕССИИ
Цель работы: на основе исходных данных построить и провести анализ нелинейных моделей парной регрессии.
Теоретические сведения
Регрессионные модели, нелинейные по включенным переменным, проводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью МНК. Рассмотрим некоторые функции.
Нелинейная логарифмическая функция
yx a b ln x |
(2.1) |
приводится к линейному виду с помощью замены
