3808

УДК 630*96

Славский, В.А. Математические методы в лесном хозяйстве и ландшафтной архитектуре [Электронный ресурс] : методические указания для самостоятельной работы студентов по направлению подготовки 35.03.01 – Лесное дело и 35.03.10 – Ландшафтная архитектура / В.А. Славский, А.В. Мироненко, М.А. Тувышкина; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ» – Воронеж, 2016. – 25 с.

Издается по решению учебно-методического совета ФГБОУ ВО «ВГЛТУ» (протокол № 7 от 15 февраля 2016 г.)

Рецензент – директор ФГБУ ВНИИЛГиСбиотех, канд. биол.наук, доц. Корчагин О.М.

Ответственный редактор д-р биол. наук, проф. С.М. Матвеев

© ФГБОУ ВПО «Воронежский

государственный лесотехнический

университет им. Г.Ф. Морозова», 2016

ВВЕДЕНИЕ

Предметом изучаемой дисциплины являются исследования варьирующих или изменяющихся (случайных) величин (признаков). Варьирование или индивидуальная изменчивость признаков – универсальное явление окружающего нас мира. В природе отсутствует однообразие, а видимое сходство между особями в растительном сообществе бывает лишь относительным. Широкой изменчивостью характеризуется и объект деятельности лесоводов – лес. В результате действия внутренних причин и внешних факторов указанные признаки носят случайный, ненаправленный характер. Чтобы разобраться в сущности таких явлений и дать им надежную (вероятную) количественную и качественную оценку, необходимо располагать соответствующими методами.

Исследование различных лесоводственно-таксационных, как правило, взаимообусловленных и взаимосвязанных признаков и лесохозяйственных процессов может быть выполнено путем моделирования. Особое место уделяется анализу одномерных эмпирических моделей, дисперсионному анализу, подбору теоретических моделей. При разработке методических указаний учтены различные аспекты современного моделирования экологических систем и изложены наиболее существенные вопросы с последующим применением ЭВМ и ГИС-технологий.

Данные методические указания составлены для студентов с целью оказания практической помощи при самостоятельном изучении этой дисциплины.

ОБЩИЕ ПОЛОЖЕНИЯ. ЦЕЛЬ И ЗАДАЧИ ДИСЦИПЛИНЫ

Целью изучения дисциплины является профессиональная подготовка бакалавров по направлениям 35.03.01 - «Лесное дело» и 35.03.10 – «Ландшафтная архитектура» в области математических методов и научных исследований, численного описания биологических и экологических массовых явлений в лесной отрасли, изучение методов научных исследований, аналитической статистики в лесном деле и ландшафтной архитектуре, изучение программного обеспечения для статистического анализа данных.

Для достижения поставленной цели решаются следующие задачи:

- ознакомление с основами применения математических методов в биологии, лесном хозяйстве и ландшафтной архитектуре;

-изучение теоретических основ математической статистики, биометрии, применительно к динамически изменяющимся явлениям в лесу;

-освоение принципов обработки массовых явлений современными математико-статистическими методами;

-освоение техники вычисления статистических показателей, построения теоретических рядов,

-освоение корреляционного, регрессионного и дисперсионного анализов

итехники их выполнения.

Студент по результатам освоения дисциплин «Математические методы в лесном хозяйстве» и «Математические методы в ландшафтной архитектуре» должен обладать следующими компетенциями:

способностью использовать основные законы естественнонаучных дисциплин в профессиональной деятельности;

способностью обосновывать принятие конкретных технологических решений при проектировании объектов лесного и лесопаркового хозяйства;

умением использовать знания о природе леса в целях планирования и проведения лесохозяйственных мероприятий, направленных на рациональное, постоянное, неистощительное использование лесов, повышение продуктивности, сохранение средообразующих, водоохранных, защитных, санитарно-гигиенических, оздоровительных и иных полезных функций лесов.

– знать: методы обработки массовых явлений; корреляционный, регрессионный и дисперсионный анализы; основы построения нормальных, ассиметричных моделей; виды теоретических и практических распределений, современные программы для статистической обработки данных.

- уметь: обрабатывать массовые наблюдения; разрабатывать простые теоретические модели на основе экосистемного подхода; оценивать адекватность и точность работы математического аппарата; использовать полученные результаты для принятия решений в конкретных производственных условиях с применением современных компьютерных программ для статистической обработки данных.

Элементы теории вероятностей

Статистические заключения, как главная составляющая метода исследования массовых явлений, имеют свои отличительные черты. Статистические заключения делают с численно выраженной определенностью.

Теоретической основой для их построения является раздел математики, изучающий закономерности случайных событий и называемый теорией вероятностей.

1 Элементы теории вероятностей

Статистические методы предполагают изучение разнообразных массовых явлений, в которых признаки изменяются от одного значения к другому, т.е. варьируют. Более глубокое изучение этих явлений показало, что предметы, особи, факты, составляющие статистическую совокупность, имеют в то же время неодинаковую повторяемость (встречаемость). Изучая толщину деревьев в каком-либо насаждении, легко убедится в том, что деревья со средним диаметром встречаются чаще, а с малым и большим диаметром – реже. Сказанное дает возможность уточнить наши понятия о статистических (случайных) величинах.

Переменная величина, принимающая различные значения с определенными вероятностями, называется случайной. Общие закономерности распределения случайных событий и случайных величин изучаются в теории вероятности.

Выше говорилось о единообразии естественных процессов - статистической устойчивости. Но, наряду с этим, действие различных случайных факторов делает элементы этих процессов (явлений) случайными.

Явления, рассматриваемые с точки зрения возможного их осуществления или неосуществления, называют событиями. Событие считается случайным, если при данных условиях оно может либо произойти, либо не произойти.

В теории вероятностей обычно используют классические примеры с бросанием монеты или кубика. Выпадение «герба» на монете или любой «цифры» на верхней стороне шестигранного кубика является случайным событием. Получение значения 20 см при обмере диаметра случайно выбранного дерева в насаждении тоже является случайным событием.

Случайные события связаны с не вошедшими в комплекс данных условий случайными факторами. Например, при исследовании естественного возобновления в лесу можно учесть такие факторы, как порода, возраст, густота насаждений, тип лесорастительных условий. Другие, неизвестные исследователю факторы, являются случайными. В данном примере это могут быть микроусловия рельефа и увлажненности почвы, воздействие диких копытных животных, очаги вредителей и болезней леса. Поэтому количественный и качественный состав естественного возобновления,

полученного на одной учетной площадке, является случайной величиной или случайным событием.

Событие считается достоверным, если оно обязательно произойдет при данных условиях. Невозможным считается событие, которое точно не произойдет при данных условиях.

В единичном случае (одно бросание монеты, одна учетная площадка) делать какие-либо выводы невозможно. При многократном повторении опыта выявляются некоторые закономерности.

Теоретическая оценка случайных величин (событий) строится на большом числе испытаний. При этом под испытанием понимают любой эксперимент, в результате которого производят наблюдения. Проводить испытания следует при неизменных условиях, что обеспечивает однородность оцениваемых событий.

Установленное в результате опыта отношение числа появлений события к общему числу испытаний называют частотой события. В таблице 1 приведены результаты бросания монеты.

Результаты подтверждают, что увеличение числа испытаний приводит частоту к определенной величине: чем больше число испытаний, тем меньше различие частот в разных сериях испытаний. При очень большом числе испытаний частота стремится к пределу, называемому вероятность.

Под «вероятностью» понимают меру возможности события, долю шансов, благоприятствующих событию. Вероятность события определяется как отношение числа случаев, при которых событие проявляется, к числу всех возможных случаев.

Из определения видно, что вероятность есть правильная положительная дробь, значение которой находится в пределах от ноля (0) до единицы (1). Если событие «А» имеет «а» благоприятных случаев и «в» – неблагоприятных, то вероятность того, что это событие произойдет, можно определить по формуле:

Отношение числа неблагоприятных случаев к числу всех возможных покажет вероятность того, что событие «А» не произойдет:

Просуммировав эти два равенства, получим:

Любая пара противоположных событий, как в данном примере, образует полную систему. Сумма вероятностей событий, образующих полную систему, равна 1.

Примером полной системы является эксперимент с монетой или кубиком. При бросании монеты вероятность выпадения «герба» (событие «А») равна Р(А)= 12 . Вероятность противоположного события «В» (выпадение «цифры»,

означающей номинал монеты) такая же: Р(В)= 12 .

Сумма вероятностей этих событий: Р(А) + Р(В)= 12 + 12 =1.

Следовательно, с вероятностью 1 монета упадет на ту или другую сторону. Так же и в случае с кубиком: вероятность появления какой-либо цифры на верхней грани Р(П)= 16 , а в сумме вероятность выпадения любой цифры равна:

Р= Р(П)= 16 16 16 16 16 16 1.

Если Р(А)= 0, то событие «А» – невозможно; если Р(А)= 1, событие обязательно осуществится, т.е. это достоверное событие.

События, вероятность которых больше 12 , считаются более вероятными;

если меньше 12 - маловероятными. Если событие имеет малую вероятность,

можно считать, что в единичном испытании оно не произойдет. Однако все зависит от того, насколько важно событие, о котором идет речь.

Вероятность того или иного события можно определять несколькими способами: статистическим, классическим и геометрическим.

1. Статистический. При этом подходе вероятность определяется через частоту появления события в большой серии испытаний. Так, в примере, описанном выше (табл. 1) частота появления «герба» при бросании монеты 4, 12 и 24 тыс. раз соответственно равнялась 0,5080; 0,5016; 0,5005. Очевидно, что она приближается к постоянному числу 12 .

Статистический подход позволяет находить вероятность событий, структура которых неизвестна. Например, только статистический подход позволил определить вероятность рождения мальчиков, равную 0,52 и девочек

–0,48.

2.Классический. При этом способе вероятность определяется через подсчет доли шансов, благоприятствующих событию. Например, при бросании кубика существует 6 равновозможных исходов, а значит, и вероятность

выпадения какой-либо цифры равна 16 . При этом подходе необходимо знать

структуру рассматриваемых событий.

3. Геометрический. Понятие об этом способе можно получить из следующего примера испытаний.

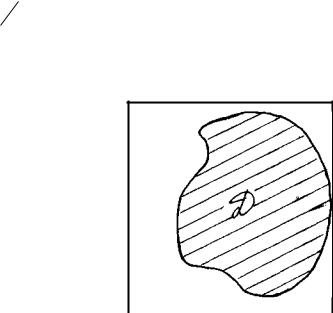
Предположим, в некотором квадрате (рис. 1) случайным образом выбирается точка. Какова вероятность того, что она окажется в области Д. Очевидно, что вероятность эта будет тем больше, чем больше область Д.

В качестве мерила вероятности здесь выступает площадь:

несовместимости и независимости событий.

Несовместимость понимается в том смысле, что если реализуется одно событие, то реализация другого невозможна (не могут произойти одновременно). Например, монета при подбрасывании не может упасть одновременно обеими сторонами, на верхней грани кубика не может одновременно выпасть две цифры и т.д. Независимое событие совершается независимо от другого события. Если имеется три независимых события, то это означает, что вероятность каждого из них не зависит от того, наступили или не наступили два других события. Три станка могут работать независимо друг от друга. При подбрасывании двух монет одновременно выпадение той или другой стороны первой монеты не зависит от вероятности выпадения ее на другой.

2 Основные теоремы о вероятности Теорема умножения вероятностей. Вероятность нескольким

независимым событиям случиться одновременно (или последовательно) равна произведению их вероятностей Р(А, В) Р(А) Р(В).

Для пояснения сущности этой теоремы воспользуемся примером с монетой. При одном бросании монеты вероятность выпадения «герба»

одновременно), как это следует из формулировки теоремы, вероятность

Покажем, что это действительно так. При подбрасывании двух монет (появление «герба» обозначим «а», а появление «цифры» – «в») возможны следующие сочетания выпадений «герба» и «цифры»: ав; ва; аа; вв.

Всего сочетаний получилось четыре, из них благоприятных (аа) – одно. Следовательно, вероятность появления «герба» при двух бросаниях равна 14 .

возможных комбинаций: вва; ваа; вав; ава; ввв; авв; аав; ааа. Как видим, всего сочетаний 8, а благоприятное (ааа) - только одно.

Теорема сложения вероятностей. Вероятность случиться одному из нескольких независимых событий без указания, какому именно, равна сумме вероятностей этих событий.

Для пояснения сущности этой теоремы воспользуемся примером с подбрасыванием кубика, на шести гранях которого нанесены цифры от 1 до 6.

Вероятность появления любой цифры Р(п) 16 .

Вероятность же появления четных цифр (2, 4, 6) будет равна:

Следовательно, задача упрощается в три раза.

3 Понятие о законе больших чисел

Одним из важнейших положений статистического метода является закон больших чисел. Смысл этого закона заключается в том, что основные закономерности, свойственные какому-либо явлению, могут проявляться при условии, если отдельные индивидуальные факты рассматриваются в достаточно большом количестве. Иначе говоря, явления, характеризующиеся

варьированием (изменчивостью), могут быть достаточно глубоко изучены только на основании множественных наблюдений.

Для практики математической статистики наибольшее применение нашли два следствия из этого закона:

1.Если имеется достаточно большой ряд независимых наблюдений, при каждом из которых вероятность отдельного события остается постоянной, то отношение числа появлений события к числу наблюдений мало отличается от вероятности события при отдельном испытании.

Это положение закона больших чисел называется теоремой Бернулли и вскрывает сущность методов математической статистики.

При отдельном испытании может оказаться как одно, так и другое событие. Но при достаточно большом числе испытаний частности появлений того или иного события приближенно равны их вероятностям. При этом следует подчеркнуть, что приближенное равенство между частностью и вероятностью имеет место лишь при достаточно большом числе наблюдений.

Примером, иллюстрирующим это следствие закона больших чисел, может служить серия множественных испытаний монеты.

2.По мере возрастания числа наблюдений распределение частностей приближается к некоторому теоретическому распределению вероятностей, выраженному коэффициентами разложения бинома определенной степени.

Чтобы разобраться в содержании второго следствия, нужно вспомнить математическую основу этого вопроса – бином Ньютона.

Асимметричные распределения

Асимметрия и крутость рядов распределений, а также двухвершинные и другие виды распределений подробно описаны в методических указаниях к лабораторным работам и разбираются во время лекционного курса. Частные случаи асимметрии – распределение Шарлье и распределение Пуассона вынесены на самостоятельное изучение.

Распределение Шарлье

Как правило, опытные распределения имеют ту или иную степень асимметрии или эксцесса. Если эти показатели оказываются больше критических значений, выравнивание опытных вариационных рядов по нормальному закону производить не рекомендуется. В этих случаях