3385

а) парабол б) дихотомии

в) простой итерации г) метод Ньютона

2.13. В чем заключается задача отделения корней? а) в установлении количества корней

б) в установлении количества корней, а также наиболее тесных промежутков, каждый из которых содержит только один корень.

в) в установлении корня решения уравнения г) в назначении количества корней

2.14.К методам уточнения корней не относится … а) метод дихотомии б) метод хорд в) метод касательных

г) метод аппроксимации

2.15.Как иначе называют метод бисекций?

а) метод половинного деления б) метод хорд

в) метод пропорциональных частей г) метод «начального отрезка» д) метод коллокации

Тема 3. Решение систем линейных алгебраических уравнений.

Студент должен:

–знать, способ решения систем линейных уравнений методом Гаусса; нахождение значения определителя системы методом Гаусса; нахождение обратной матрицы методом Гаусса;

–уметь решать системы линейных уравнений приближенными методами. Рекомендуемая литература – 1о, с. 99-133; 1д, с. 48-58, 189-197, 2д, с. 103-

105.

Задание для самопроверки

1.Опишите в тетради для самостоятельной работы:

Основные методы решения линейных алгебраических уравнений.

2.Выберите один из альтернативных ответов.

2.1. Для решения систем линейных уравнений по правилу Крамера необходимо следующее:

а) определитель матрицы системы не равен нулю

12

б) найти разрешающую формулу в) выразить первую производную г) задать точность вычислений e>0

2.2.Метод Зейделя решения систем линейных уравнений является . . .

а) точным б) приближенным

в) итерационным г) прямым

2.3.Какой метод решения систем линейных уравнений состоит из 2-х этапов (прямой и обратный ход)?

а) метод Зейделя б) метод Гаусса в) правило Крамера

г) метод простой итерации

2.4.Для систем линейных уравнений с плотно заполненной матрицей коэффициентов порядка n<200 целесообразно применять …

а) метод Зейделя б) метод Гаусса в) метод прогонки

г) метод простой итерации

2.5.Для обеспечения сходимости итерационного процесса в методе Зейделя для систем линейных уравнений достаточно выполнения условия

а)

б)

в)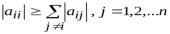

2.6.Условие 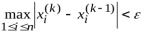является условием прекращения вычислений для метода

а) Зейделя б) Гаусса в) прогонки г) Ньютона

2.7.Неизвестные в методе Гаусса определяются по формуле

а)

б) в)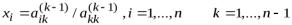

г)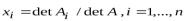

2.8. Метод Зейделя требует

13

а) составления приведенной системы б) разрешения каждого уравнения относительно диагональной

неизвестной в) нахождения второй производной

2.9. Метод Зейделя является самоисправляющимся, т.е.

а) отдельная вычислительная ошибка не отражается на конечном результате

б) при возникновении ошибок итерационный процесс становится циклическим

в) ошибочное приближение принимается за новый вектор

2.10.Метод Гаусса применим, если а) матрица системы невырождена б) система является несовместной

в) определитель системы равен нулю

2.11.Какой метод решения систем линейных уравнений требует предварительной проверки системы уравнений на сходимость:

а) простой итерации б) Гаусса в) Зейделя г) прогонки

2.12.Рекуррентная формула для поиска n – й неизвестной k+1 – го приближения имеет вид:

а) б)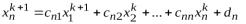

в) 2.13. Дополните

… решения систем линейных уравнений требует записи исходной

системы в виде . а) метод простой итерации б) метод Гаусса в) метод Зейделя г) метод прогонки 2.14. Дополните

… решения СЛАУ требует задавать начальное приближение – вектор X0 =

().

а) метод простой итерации б) метод Гаусса в) метод Зейделя г) метод прогонки

14

Тема 4. Интерполирование и экстраполирование функций.

Обучающийся должен:

–знать, принципы составления интерполяционных формул Лагранжа; составление интерполяционных формул Ньютона; принципы интерполяции функцию сплайнами и нахождение ее значение в заданной точке;

–уметь составлять интерполяционные формулы Лагранжа, Ньютона, находить интерполяционные многочлены сплайнами.

Рекомендуемая литература – 1о, с. 154-163, 1д, с. 175-181.

Задание для самопроверки

1.Опишите в тетради для самостоятельной работы:

Понятия интерполирования и экстраполирования.

2.Выберите один из альтернативных ответов.

2.1. Интерполяция – это… а) способ нахождения промежуточных значений величины по

имеющемуся дискретному набору известных значений б) продолжение функции, принадлежащей заданному классу, за пределы

ее области определения.

в) замена одних математических объектов другими, в том или ином смысле близким к исходным.

г) метод решения задач, при котором объекты разного рода объединяются общим понятием.

2.2.Интерполяция бывает:… а) кусочная и локальная б) локальная и глобальная в) кусочная и априорная

г) максимальная пи минимальная

2.3.Итерация – это ….

а) повторение. Результат повторного применения какой–либо математической операции.

б) замена одних математических объектов другими, в том или ином смысле близким к исходным.

в) число, изображаемое единицей и 18 нулями г) продолжение функции, принадлежащей заданному классу, за пределы

ееобласти определения.

2.4.Конечными разностями первого порядка называют а) сумму соседних узлов интерполяций

б) разность между значениями функций в соседних узлах интерполяции в) сумму между значениями функций в соседних узлах интерполяции г) произведение значений трех соседних узлов интерполяции

15

2.5. Найди в формуле интерполяционного многочлена Лагранжа ошибку

г) Нет ошибки в формуле 2.6. Конечными разностями первого порядка называют

а) Сумму соседних узлов интерполяций б) Разность между значениями функций в соседних узлах интерполяции

в) Сумму между значениями функций в соседних узлах интерполяции г) Произведение значений трех соседних узлов интерполяции

2.7. Задача интерполяции f(x) состоит в выборе функции g(x), которая:

а) отклонялась бы от f(x) в точках не более , чем на некоторое заданное число ;

б) была бы непрерывна на некотором заданном отрезке и принимала бы значения f(x) точках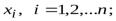

в) принимала бы значения f(x) точках

г) была бы непрерывна на некотором заданном отрезке и принимала бы

значения f(x) точках с некоторой заданной точностью. 2.8. Узлы интерполяции это:

а) значение функции у =f(x) в некоторых точках

б) значения аргументов xi ,для которых известны значения интерполируемой функции f(xi);

в) любое значение xi, i=1,2,…n, из области определения f(x); г) фактор xi, i=1,2,…n исследуемых явлений y = f(x) ;

д) промежуточные значения y =f(x);

2.9. Геометрически задача интерполяции означает :

а) построение кривой, проходящей через заданное множество точек (xi, yi), i=1,2,…n;

б) построение интервала, в котором определена заданная функция ;

в) построение прямой, проходящей через узлы интерполяции xi ,i=1,2,…n; г) построение множества кривых проходящих через заданное множество

точек (xi, yi ), i=1,2,…, n;

2. 10. Какой класс приближающих функции чаще всего применяют при интерполировании?

16

а) полиномиальные функции, коэффициенты которых зависят от координат и значений функции в узлах;

б) тригонометрические функции, имеющие отношение к рядам Фурье; в) логарифмические функции.

2.11.Какой критерий согласия применяется при интерполировании функции полиномами?

а) уменьшение максимального отклонения значений интерполирующей функции в узлах интерполяции до минимума;

б) минимизация суммы квадратов отклонений в узловых точках; в) точное совпадение в узловых точках

2.12.При интерполяции с помощью интерполяционного полинома

Лагранжа а) узлы, между которыми производится интерполяция, должны

располагаться только равномерно на отрезке интерполяции

б) узлы хi должны быть пронумерованы в порядке возрастания аргумента

х

в) координаты хi должны образовывать монотонную последовательность

чисел

г) узлы хi могут располагаться на оси ординат произвольным образом, но не должны совпадать друг с другом

2.13.Интерполяционные формулы могут быть использованы

а) только в пределах между крайними узлами интерполяции б) для значений аргумента, лежащих как в пределах, так и за пределами

крайних узлов интерполяции в) только в окрестностях узлов интерполяции, в пределах которых

разложение в ряд Тейлора не приводит к большим ошибкам 2.14. Локальная интерполяция отличается от глобальной

а) большими погрешностями при использовании полиномов той же степени

б) меньшими степенями интерполирующих полиномов в) могут скачком измениться значения производных на концах отрезков

интерполирования

Тема 5. Численное интегрирование

Обучающийся должен:

–знать, формулу прямоугольников; формулу трапеций; формулу парабол (Симпсона);

–уметь вычислять интегралы методами численного интегрирования (при помощи формул Ньютона-Котеса).

Рекомендуемая литература – 1о, с. 163-182, 1д, с. 183-189, 2д, с. 315-328.

Задание для самопроверки

17

1.Опишите в тетради для самостоятельной работы:

Основные методы вычисления интегралов.

2.Выберите один из альтернативных ответов.

2.1.Все методы вычисления интегралов делятся на: а) точные и приближенные б) прямые и итеративные в) прямые и косвенные

г) аналитические и графические д) приближенные и систематические

2.2.Точный метод вычисления интегралов был предложен: а) Ньютоном и Лейбницем б) Ньютоном и Гауссом в) Гауссом и Стирлингом г) Вольтерром д) Гауссом и Крамером

2.3.Приближенные методы вычисления интегралов можно разделить на 2

группы:

а) аналитические и численные б) аналитические и графические в) систематические и численные г) систематические и случайные

д) приближенные и неприближенные

b

2.4. Что это за формула I f (x)dx a

а) формула Ньютона - Лейбница б) формула Ньютона - Котеса в) формула Симпсона г) формулы не существует

2.5. Формула Симпсона – это…

г) формулы не существует 2.6. В методе Симпсона подынтегральная функция заменяется ... .

а) квадратичной параболой б) прямой в) кубической параболой

г) выражением, содержащим тригонометрические функции

18

2.7.Погрешность вычисления определенного интеграла можно уменьшить, если ... .

а) увеличить число точек разбиений интервала б) повысить степень используемых для интегрирования полиномов в) уменьшить число точек разбиений интервала

г) понизить степень используемых для интегрирования полиномов

2.8.Задача приближенного интегрирования состоит в вычислении ... .

а) определенного интеграла по значениям подынтегральной функции в

узлах

б) интегральной суммы, заменяющий определенный интеграл на данном интервале

в) неопределенного интеграла по значениям подынтегральной функции в

узлах

г) определенного интеграла по значениям подынтегральной функции в произвольных точках

д) корней системы линейных алгебраических уравнений на данном интервале

2.9.Подынтегральная функция f(х)=х2. Применение какого численного метода даст наиболее точное вычисление интеграла?

а) Симпсона б) трапеций

в) правых прямоугольников г) левых прямоугольников д) средних прямоугольников

2.10.Основными понятиями численного интегрирования являются:

а) узел б) квадратурная формула

в) интерполяционный многочлен г) коэффициенты регрессии

Тема 6. Численное решение обыкновенных дифференциальных уравнений.

Обучающийся должен:

–знать, метод Эйлера; метод Рунге-Кутта;

–уметь приближенно находить решение обыкновенного дифференциального уравнения первого порядка.

Рекомендуемая литература – 1о, с. 133-146, 1д, с. 181-183; 2д, с. 359-368.

Задание для самопроверки

2. Опишите в тетради для самостоятельной работы:

Основные методы решения обыкновенных дифференциальных уравнений.

19

2. Выберите один из альтернативных ответов.

2.1.Что является решением дифференциального уравнения? а) уравнение первого порядка

б) уравнение первого порядка, разрешенное относительно производной в) уравнение второго порядка г) уравнение второго порядка, разрешенное относительно производной

2.2.Золотое сечение – это…

а) такое пропорциональное деление отрезка на части, при котором меньший отрезок относится к большему, как больший ко всему.

б) непропорциональное деление отрезка на части, при котором меньший отрезок относится к большему, как больший ко всему.

в) непропорциональное деление отрезка на части, при котором больший отрезок относится к меньшему, как больший ко всему.

г) такое пропорциональное деление отрезка на части, при котором больший отрезок относится к меньшему, как больший ко всему.

2.3. В основе какого метода лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной форме?

а) метод Лагранжа б) метод границ в) метод Коши г) метод Эйлера

2.4. Формула Рунге-Кутта это:

а) yi 1 yi 16 (r1 2r2 2r3 r4) б) yi 1 yi 16 (r1 3r2 4r3 r4) в) yi 1 yi 19 (2r1 2r2 2r3 r4) г) yi 1 yi 16 (r1 2r2 2r3 r4)

2.5.Метод Эйлера относится к а) одношаговым б) задаче Коши в) многошаговым

г) аналитическому д) краевой задаче

2.6.Удобство применения метода Эйлера при решении уравнения заключается в следующем:

а) нет необходимости выражать производные высоких порядков для правой части в аналитическом виде

б) нет необходимости выражать первой производной для правой части в аналитическом виде

20

в) знание аналитического выражения для первой производной правой части уравнения

г) знание аналитического выражения для производной любого порядка правой части уравнения

2.7. В методе Эйлера с каждым шагом а) решение отдаляется от точного решения

б) решение приближается к точному решению в) расхождение с вычисленным и точным решениями остаётся

постоянной

2.8.Метод прогонки разработан для решения дифференциальных

уравнений:

а) 1-го порядка б) 2-го порядка в) 3-го порядка г) 4-го порядка д) 5-го порядка

6) любого порядка

2.9.Содержание метода прогонки заключается в

а) в приведении к задачам Коши б) в решении методами конечных разностей в) в аналитическом решении

г) в решении трёхчленной линейной системы

2.10.Решение по методу прогонки состоит из а) прямого хода б) обратного хода

в) в приведении исходного уравнения к трёхчленной линейной системе г) в приведении к задачам Коши

2.11.Метод прогонки

а) обладает устойчивым вычислительным алгоритмом б) чувствителен к ошибкам округления

в) в приведении исходного уравнения к трёхчленной линейной системе г) в приведении к задачам Коши

2.12. В методе прогонки решения для промежуточных значений аргумента находят

а) интерполированием б) применением интерполяционной формулы Ньютона в) экстраполированием г) решая методом Эйлера

д) решая методом Рунге-Кутта

Критерии оценки выполненного задания