
3012
.pdfМинистерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный лесотехнический университет имени Г. Ф. Морозова»
МАТЕМАТИКА (СПЕЦИАЛЬНЫЕ РАЗДЕЛЫ)
Решение дифференциальных уравнений методом операционного исчисления
Методические указания к лабораторным работам для студентов по направлению подготовки
15.03.04 – Автоматизация технологических процессов и производств
Воронеж 2018
УДК 517.2+517.4
Веневитина С. С. Математика (специальные разделы). Решение дифференциальных уравнений методом операционного исчисления [Электронный ресурс] : метод. указания к лаб. работам для студентов по направлению подгот. 15.03.04 – Автоматизация технол. процессов и пр-в. / С. С. Веневитина, И.В. Сапронов; ВГЛТУ. – Воронеж, 2018. – 36 с. – Электронная версия в ЭБС ВГЛТУ.
Рецензент заведующий кафедрой математического моделирования ВГУ, д-р физ.-мат. наук, проф. В.А. Костин
Методические указания к лабораторным работам по дисциплине «Математика (специальные разделы)» предназначены для студентов ФГБОУ ВО «Воронежский государственный лесотехнический университет им. Г.Ф.
Морозова», обучающихся по направлению подготовки 15.03.04 |
– |
«Автоматизация технологических процессов и производств». |
|
Материалы данной учебно-методической разработки по содержанию, форме изложения и объёму соответствуют задачам дисциплины и требованиям стандарта соответствующего направления подготовки.
3
Введение
Операционное исчисление является одним из разделов математического анализа. Его методы применяются в прикладной математике, в технической физике, в биологии, в инженерных дисциплинах. Особенно широкое применение операционное исчисление находит в современной автоматике и телемеханике.
Наиболее обширную область приложения операционного исчисления составляют линейные дифференциальные уравнения с постоянными коэффициентами, а также системы таких уравнений. Решение дифференциального уравнения (или системы дифференциальных уравнений) сводится к решению простого алгебраического уравнения (системы уравнений), причем начальные условия учитываются с самого начала процесса решения.
§ 1. Оригинал и изображение
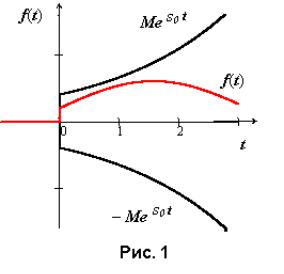
Определение. Оригиналом будем называть действительную функцию действительного аргумента f(t), удовлетворяющую условиям:
1)f (t) ≡ 0 при t < 0;
2)существуют такие числа M >0 и s0 ≥ 0, что для всякого t ≥ 0
выполняется неравенство | f (t) |≤ Mes0t .
3)на любом конечном отрезке [a, b] положительной полуоси Ot
функция f(t) удовлетворяет условиям Дирихле, т.е.
а) ограничена; б) либо непрерывна, либо имеет
лишь конечное число точек разрыва первого рода;
в) имеет конечное число экстремумов.
Пример функции-оригинала изображен на рис. 1.
Наименьшее из чисел s0, при которых выполняется неравенство, называется показателем роста функции f(t).
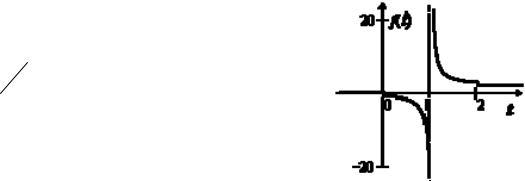
4
Определение. Изображением функции f(t) называется функция F(p) комплексного переменного p, которая определяется равенством
|
F( p) = ∞∫ f (t)e−pt dt |
при |
Re p > s0 . |
(1) |
|||
|
|
0 |
|
|
|
|
|
Можно показать, что при выполнении условий 1-3 несобственный |
|||||||
интеграл |
∞∫ f (t)e−pt dt |
сходится |
абсолютно |
при |
Re p = s > s0 , |
если |
|
|
0 |
|
|
|
|
|
|
| f (t) |≤ Mes0t . Операция |
перехода |
от |
оригинала f(t) |
к изображению |
F(p) |
||
называется преобразованием Лапласа. Теорию преобразования Лапласа называют операционным исчислением.
Соответствие между оригиналом и его изображением обозначают
символически |
f (t ) → F ( p ) |
или |
F ( p ) → f (t ) . Можно также |
писать |
|||||||||||||||||
L{ f (t )} = F ( p ) . заметим, |
что |
это |
|
соответствие является |
взаимно |
||||||||||||||||
однозначным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1. Функция f (t) = ch(3 +5i)t является оригиналом, так как она |
|||||||||||||||||||||
непрерывна при t ≥ 0 |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
| ch(3 +5i)t |= |
|
e(3+5i)t +e−(3+5i)t |
|
≤ |
|
|
e3t+5ti |
|
|
+ |
|
|
e−3t−5ti |
|
|
= e3t + e−3t ≤ e3t . |
|||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
||||||||||
Здесь M=1 , s0=3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Рассмотрим функцию |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
0, t |
< 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (t ) = |
1 |
|
|
, t ≥ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эта функция не является оригиналом, так как она имеет разрыв второго рода в точке t = 1 (см. рис. 2).
Пример 3. Рассмотрим функцию
|
0, t < 0; |
|
|
||
f (t ) = |
(t + 1) et |
2 |
, t |
≥ 0. |
Рис. 2 |
|
|
||||
Эта функция не является оригиналом, так как не существует таких констант M >0 и s0 ≥ 0, что | f (t) |≤ Mes0t .
5
Пример 4. Рассмотрим функцию
0, t < 0; f (t ) = ≥
sin( 1 t ), t 0.
Эта функция не является оригиналом, так как она имеет бесконечное число
экстремумов на отрезке [0,1]. |
|
|
|
|
|
|
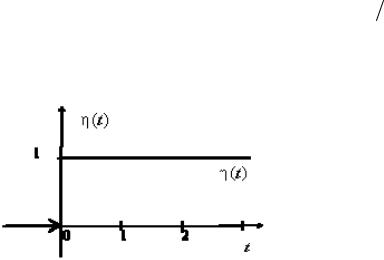
Определение. |
Единичной функцией |
|
|
|
Хевисайда называется функция вида |
||
|
|
|
|
0, t < 0; |
|
|
η (t ) = |
1, t ≥ 0. |
|
|
|
|
|
|
|
|
Функция η(t) |
является оригиналом, так |
|
|
|
как она удовлетворяет условиям 1-3 с |
||
|
|
константами M=1 и s0=0 |
|
|
|
|
|
||
|
Рис. 3 |
С ее помощью можно любую функцию, |
||
удовлетворяющую только условиям 2 и 3, превращать в оригинал, удовлетворяющий уже всем условиям определения. Это делается с помощью выражения
|
0, t < 0; |
ϕ (t )η (t ) = |
|
ϕ (t ), t ≥ 0. |
|
Однако в дальнейшем для простоты |
записи вместо ϕ(t)η(t) будем |
писать ϕ(t) , считая, что при t<0 эти функции равны нулю. Например, вместо
оригинала sin ωtη(t) будем писать просто sin ωt , |
имея в виду, |
что и эта |
|||||||||||||
функция является оригиналом. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 5. Найдем изображение функции Хевисайда |
|
|
|||||||||||||
|
η(t) → ∞∫η(t)e−pt dt = ∞∫1 e−pt dt = limb→∞ ∫b e−pt dt = |
|
|
||||||||||||
|
0 |
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
e |
− pt |
|
|
b |
|
|
|
|
|||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||
|
= lim |
|
|
|
|
= lim |
1 |
− |
1 |
e−pb . |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
b→∞ − p |
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
b→∞ p p |
|
|
|
||||||||
|
|
|
|
|
1 |
|
|||||||||
Если Re |
p > 0 , то lim e− pb = 0 и в этом случае будем иметь η(t) → |
. |
|||||||||||||
|
|||||||||||||||
|
b→∞ |
|
|
|
|
|
|
|
|
|
|
p |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, 1 → |
1 |
при |
|
Re p > 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 6. Найдем изображение функции eαt . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
b |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
αt |
|
|
|
|
|
αt |
|
|
− pt |
|
|
|
|
(α− p)t |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(α− p)t |
|
|
|
|||||||||||||
e |
|
→ ∫e |
|
e |
|
|
dt = ∫e |
|
|
dt |
= lim |
|
|
|
|
|
e |
|
|
|
= |
|
|||||||||||
|
|
|
|
|
|
|
− p |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
b→∞ α |
|
|
|
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= lim |
|
1 |
|
|
(e(α−p)b −1)= |
|
|
1 |
(lim |
e(α−p)b |
−1) |
= |
|
|
1 |
|
, |
|
|
|
|||||||||||||
|
|
|
|
α − p |
α − p |
|
|
|
|||||||||||||||||||||||||
b→∞ α − p |
|
|
|
|
|
|
b→∞ |
|
|
|
|
|
|
|
|
||||||||||||||||||
Так как limb→∞ |
e(α−p)b |
= 0 при условии Re p > Re α , если α – комплексное |
|||||||||||||||||||||||||||||||
число. Если α – |
действительное число, то при условии |
|
Re p > α . Таким |
||||||||||||||||||||||||||||||
образом, |
e |
αt |
→ |
|
|
|
1 |
|
|
при Re |
p > Re α . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
α − p |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
§ 2. Свойства преобразования Лапласа |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
1. |
|
|
|
Линейность. |
Если |
|
|
f1 (t ) → F1 ( p ) |
|
и |
|
f 2 (t ) → F2 ( p ) , |
то |
||||||||||||||||||||
C 1 f1 (t ) + C 2 f 2 (t ) → C 1 F1 ( p ) + C 2 F2 ( p ) , |
|
|
где |
|
C1 , |
|
C2 |
– |
|||||||||||||||||||||||||
постоянные числа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
C1 f1 (t ) + C 2 f 2 (t ) → ∞∫ (C1 F1 ( p ) + C 2 F2 ( p )) e − pt dt = |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= C1 ∫ F1 ( p)e−pt dt +C2 ∫ F2 ( p)e−pt dt = C1F1 ( p) +C2 F2 ( p). |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 7. Найти изображение оригиналов sin t , cost , |
sh t |
и ch t . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение. Выразим |
|
|
sin t |
через показательные функции sin t |
= |
eit −e−it |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2i |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как e |
it |
→ |
|
|
|
1 |
|
|
|
|
|
и |
|
e |
−it |
→ |
|
|
1 |
|
|
|
|
|
, |
|
|
|
то, |
|
|
учитывая |
|
свойство |
линейности |
|||||||||||||||||||||||||||||||||||||||||||
|
|
p −i |
|
|
|
|
|
p +i |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
изображения, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2i |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
sin t → |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
= |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
2i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2i p |
|
+1 p |
2 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
p −i |
|
|
|
p +i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Аналогично, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cost = |
eit |
+e−it |
|
|
; |
|
|
|
|
sh |
t = |
et −e−t |
|
|
|
; |
|
ch t = |
et +e−t |
. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
cost → 1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
2 p |
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
= |
|
|
|
|
|
|
= |
|
|
|
|
; |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 p |
|
|
+1 p |
|
+1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
p |
−i p +i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
sh t → |
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
−1 |
|
|
|
p +1 |
|
|
|
|
2 p |
−1 p |
+1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
ch t → |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
2 p |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
= |
|
|
|
= |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
−1 |
|
|
|
p +1 |
|
|
|
|
2 p |
2 |
− |
1 p |
2 |
−1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
sin t → |
|
|
1 |
|
|
|
|
; |
|
|
|
cost → |
|
|
|
|
|
|
p |
|
|
|
; |
|
|
|
sh |
|
|
|
t → |
|
1 |
|
|
; |
ch |
t → |
p |
. |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 +1 |
|
|
|
|
|
|
|
p2 +1 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 −1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
p2 +1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
p |
|
||
2. Подобие. Если |
f (t ) → F ( p ) , то |
f (at ) → |
|
F |
|
|
для |
|
a |
a |
|||||||
|
|
|
|
|
|
|||
любого a>0.

8
Доказательство.
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
p |
t1 |
1 |
|
|
|
1 |
|
∞ |
|
|
|
|
|
p |
t1 dt1 = |
||||||
|
f (at ) = ∫ f (at ) e − pt dt = ∫ f (t1 ) e − |
|
|
dt1 |
= |
|
∫ f (t1 ) e − |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
a |
|
a |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a |
a |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
|
|
F |
|
|
|
|
|
|
= at ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
a (здесь t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
f (at ) → |
1 |
F |
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Итак, |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Пример 8. Найти изображение оригинала |
|
sin ωt . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
Решение. Известно, что |
sin t |
→ |
|
|
|
|
1 |
|
|
|
. Пользуясь свойством подобия, |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
p |
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
sin ωt → |
1 |
|
|
|
1 |
|
|
|
|
|
|
= |
|
|
|
|
ω 2 |
|
|
|
= |
|
ω |
|
|
|
. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
ω |
p |
2 |
|
+ 1 |
|
ω ( p 2 |
+ ω 2 ) |
|
p 2 |
|
+ ω 2 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, sin ωt |
→ |
|
|
|
|
|
ω |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
p |
2 |
+ ω |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Аналогично можно получить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
cos ωt → |
|
|
|
|
p |
|
|
|
|
; |
sh ωt → |
|
|
|
ω |
|
|
|
; |
ch ωt → |
|
|
|
p |
|
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
p |
2 |
+ ω |
2 |
|
p |
2 |
|
|
2 |
|
p |
2 |
− ω |
2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− ω |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3. |
Смещение |
изображения. |
Если |
f (t ) → F ( p ) , |
то |
|
e λt f (t ) → F ( p − λ ) |
для любого |
комплексного числа |
λ |
при |
||
Re p > s0 + Re λ . |
|
|
|
|
|
|
Доказательство. |
|
|
|
|
|
|
e λt f (t ) → ∞∫e λt f (t ) e − pt dt = ∞∫ f (t ) e − p ( t − λ ) dt = F ( p − λ ). |
||||||
|
0 |
|
0 |
|
|
|
Итак, e λt f (t ) → F ( p − λ ) .
9 |
|
|
|
|
|
|
|
|
|
Пример 9. Найти изображение оригинала e λt |
sin ωt |
||||||||
Решение. Так как sin ωt → |
|
|
|
ω |
|
|
, |
то используя свойство |
|
p |
2 |
+ ω |
2 |
||||||
|
|
|
|
|
|
||||
смещения, получим |
|
|
|
|
|
|
|
|
|
e λt sin ωt → |
|
|
|
|
ω |
|
. |
||
|
|
|
|||||||
|
( p − λ ) 2 |
+ ω 2 |
|||||||
4. |
|
|
Запаздывание |
оригинала. |
|
Если |
f (t ) → F ( p ) , |
то |
||
f (t − t0 ) → e −t 0 p F ( p ) |
для |
0 ≤ t0 < ∞ , то есть запаздывание оригинала |
||||||||
на положительную величину |
t0 соответствует умножению изображения на |
|||||||||
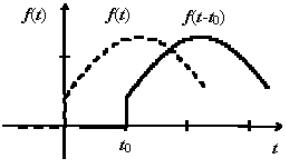
e−t0 p . График функции |
y = f (t −t0 ) сдвинут по оси t относительно графика |
|||||||||
функции y = f (t) вправо на величину t0 (см. рис. 4). |
|
|
|
|||||||
|
|
|
|
|
Доказательство. Функция f (t −t0 ) , |
|||||
|
|
|
|
|
как и |
|
f (t) , |
удовлетворяет |
условиям, |
|
|
|
|
|
|
наложенным |
на |
оригинал, |
|||
|
|
|
|
|
следовательно, |
для нее |
существует |
|||
|
|
|
|
|
изображение |
|
|
|
||
|
|
|
Рис. 4 |
|
t0 |
|
|
|
|
|
|
|
|
∞ |
|
|
|
∞ |
|
|
|
f (t −t0 ) → ∫ f (t −t0 ) e−pt dt = ∫ f (t −t0 ) e−pt dt + ∫ f (t −t0 ) e−pt dt . |
|
|||||||||
|
|
|
0 |
|
0 |
|
|
t0 |
|
|
Первый интеграл |
равен нулю, так |
как по |
определению |
оригинала |
||||||
f (t −t0 ) = 0 |
при t < t0 . |
|
|
|
|
|
|
|
||
∞∫ f (t −t0 ) e−pt dt = ∞∫ f (t1 ) e−p(t1 +t0 ) dt1 = e−pt0 |
∞∫ f (t1 ) e−pt1 dt1 = e−t0 p F( p) |
|
||||||||
t0 |
0 |
|
|
|
0 |
|
|
|
||
(здесь t1 = t −t0 ). |
|
|
|
|
|
|
|
|||
Итак, |
f (t − t0 ) → e −t 0 p F ( p ) . |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
Пример 10. Найти изображение оригинала η(t −3) . |
|
|
|
|
||||||||||||||||
Решение. |
Так |
как |
η(t) → |
|
|
1 |
, |
то, |
используя |
свойство запаздывания, |
||||||||||
|
|
p |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
получим η(t − |
3) → |
e−3 p |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример |
11. |
По |
данному |
|
|
изображению e |
−5 p |
|
|
p |
|
определить |
||||||||
|
|
|
p |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
|
||
оригинал. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
Известно, что |
|
|
|
|
p |
|
|
→ cos t . |
Применяя |
свойство |
|||||||||
|
|
|
p |
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
|
|
|||
запаздывания, |
получим |
e−5 p |
|
|
|
|
p |
|
→ cos(t −5) |
при |
|
t ≥5 , |
при t <5 |
|||||||
|
p |
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
||||
оригинал равен нулю.
5.Дифференцирование оригинала. Если f (t ) → F ( p ) и
существует функция f ′(t) , являющаяся оригиналом, то f ′(t) → pF( p) − f (0) ,
где |
f (0) = lim f (t) . |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
t→0+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∞ |
|
|
|
|
|
u = e− pt |
du = −pe−pt dt |
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
f ′(t) → ∫ f ′(t) e−pt dt = |
= |
|
||||||||||||
|
|
|
′ |
|
|
|
|
||||||||
|
|
0 |
|
|
|
|
|
dv |
= |
f (t)dt |
v = |
f (t) |
|
|
|
|
= lim f (t)e−pt − |
|
f (0) |
|
|
∞ |
f (t)e−pt dt = pF( p) − f (0). |
|
|||||||
|
|
+ p |
|
|
|||||||||||
|
|
|
0 |
|
|||||||||||
|
t→∞ |
|
|
|
e |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
||
|
Итак, |
f ′(t) → pF( p) − f (0) . |
|
|
|
|
|
|
|
||||||
|
Замечание. |
lim f (t)e− pt = 0 , |
так |
как |
f (t) |
- оригинал |
и поэтому |
||||||||
|
|
|
t→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
выполняется |
условие |
|
2: | f (t) |≤ Mes0t . |
При |
Re p = s > s0 |
выполняется |
|||||||||
| f (t)e− pt |=| |
f (t) | e−st |
< Mes0t e−st |
= Me(s0 −s)t → 0 |
при t →∞ . |
|
||||||||||
