
1976
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Воронежская государственная лесотехническая академия»
ГИДРОТЕХНИЧЕСКИЕ МЕЛИОРАЦИИ
Методические указания для самостоятельной работы студентов специальностей 250201 – Лесное
хозяйство, 250203 – Садово-парковое и ландшафтное строительство; по направлению подготовки 250100 – Лесное дело
Воронеж 2012
УДК 630*237
Дюков А.Н. Гидротехнические мелиорации. Методические указания для самостоятельной работы студентов специальностей 250201 – Лесное хозяйство, 250203 – Садово-парковое и ландшафтное строительство; по направлению подготовки 250100 – Лесное дело/А.Н. Дюков, П.Ф. Андрющенко, Е.А.Михина, Т.А.Малинина, Т.П.Деденко. – Воронеж, 2012. –
32 с.
Печатается по решению редакционно-издательского совета ВГЛТА
Рецензент: проф. доктор с.-х. наук А.Ю. Черемисинов каф. мелиорации и геодезии ВГАУ
Науч. редактор, д-р с.-х- наук, проф. Я.В. Панков
УДК 630*237
Дюков А.Н. Андрющенко П.Ф. Михина Е.А. Малинина Т.А. Деденко Т.П., 2012
Воронежская государственная лесотехническая академия,2012
ВВ Е Д Е Н И Е
Внашей стране большое внимание уделяется вопросам повышения продуктивности лесов. Гидротехнические мелиорации лесных земель в сочетании с лесохозяйственными, лесокультурными, лесомелиоративными
идругими мероприятиями являются мощным средством увеличения прироста древесины и улучшения ее качества. Кроме того, они создают благоприятные условия для лесовосстановления, лесоэксплуатации,
улучшения путей транспорта, расширения лесистости в засушливых районах, улучшению качества древесины на осушаемых землях и в целом содействуют повышению интенсификации лесного и сельского хозяйства.
При помощи гидротехнических мелиораций водному хозяйству лесных предприятий придается комплексный характер, то есть водные ресурсы используются для регулирования влажности почв на лесных и сельскохозяйственных землях, обводнения, противопожарных мероприятий,
водного транспорта, улучшение санитарно-гигиенических и эстетических свойств лесных площадей. Отсюда понятно, как велико значение дисциплины «Гидротехнические мелиорации лесных земель».
Для своей успешной производственной деятельности студенты должны самостоятельно научиться - правильно использовать водные ресурсы в лесном хозяйстве, для бытовых нужд лесничеств и при орошении питомников; участвовать в разработке проектов мелиорации; устраивать простейшие мелиоративные системы.
Самостоятельному изучению курса должно предшествовать также самостоятельному изучению тесно связанных с ним дисциплин: геодезии,
лесной метеорологии, почвоведения, лесоводства, лесной таксации и лесоустройства, лесных культур. Кроме того, для успешного освоения специальных частей курса необходимо детально изучить вопросы гидравлики, гидрологии, гидрометрии, а также осушения, оводнения и орошения.
1. ГИДРАВЛИКА
Гидравликой называется наука изучающая законы равновесия и движения жидкостей и разрабатывающая способы применения этих законов к решению различных практических задач.
Гидравлика делится на две составные части: гидростатику и гидродинамику. Гидродинамикой называется та часть гидравлики, в
которой изучаются законы движения жидкостей. Гидростатикой называется та часть гидравлики, в которой изучаются законы равновесия и покоя жидкостей. На законах гидравлики основаны расчеты каналов,
гидротехнических сооружений, водопроводов, водосбросов, ступенчатых перепадов и т.д.
1.1 Гидростатика
1.1.1Физические свойства жидкостей
Жидкость как всякое материальное тело обладает физическими свойствами. При изучении этого раздела следует особо остановиться на свойствах, лежащих в основе узловых закономерностей и процессов гидравлики: объемный вес, объемная масса, плотность, сжимаемость,
вязкость.
Примеры решения задач.
Пример 1.
Объем воды равен W = 0,9 м3 объемный вес γ = 997 кг/м3 = 0,997
т/м3. Необходимо определить вес воды, G = ?
Решение: G = W * γ = 0,9 * 0,997 = 0,8973 т
(Ответ: G = 0,8973 т)
Пример 2.
Плотность керосина 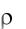 = 76,5 кг * сек2/ м4 . Чему равен объемный
= 76,5 кг * сек2/ м4 . Чему равен объемный
вес?
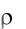
Решение: |
γ = m * g /W = γ *g , |
γ = 76,5 * 9,81 = 750 кг/м3
(Ответ: γ = 0,75 т/м3)
Пример 3.
Определить полное, избыточное и маномитрическое давление в точке А, находящейся на глубине h = 2 м под свободной поверхностью.
Жидкость – пресная вода. На свободную поверхность действует атмосферное давление Ра.
Решение:
1.Полное гидростатическое давление определяем по формуле:
Р= Ро + γ h,
где: Ро = Ра = 1,03 * 105 Па; γ = 0,001 кг/см3; h = 200 см, т.е.
Р= 1,03 + 0,001 + 200 = 1,23 * 105 Па
2.Избыточное гидростатическое давление по формуле:
Риз = Р – Ра Риз = 1,23 * 105 – 1,03 * 105 = 0,2 * 102 Па
3. Манометрическое давление по формуле: Рм = Р – Ра
Рm = 1,23 * 105 – 1,03 * 105 = 0,2 * 102 Па
(Ответ: Р=1,23 * 105 Па; Риз = Рм = 0,2 * 102 Па)
Пример 4.
Определите все виды гидростатического давления в баке с нефтью на глубине h = 3 м, если на свободной поверхности нефти давление с учетом
атмосферного, Ро = Рm + Ра = 2,03 * 105 Па. Вес единицы объема нефти γ =
0,9 т/м3.
Решение:
1.Полное гидростатическое давление:
Р= Ро + γ h = 2,03 * 105 + 0,9 * 3 = 4,7 * 105 Па
2.Избыточное гидростатическое давление:
Риз = γ h = 0,9 * 3 = 2,7 т/м3
3. Манометрическое давление внутри жидкости на глубине 3 м:
Рm = Р – Ра = 22,7 – 10,0 = 12,7 т/м2 = 1,27 кг/см2 = 1,3 * 105 Па
4.Манометрическое давление над свободной поверхностью:
Рm = Ро – Ра = 20 – 10 = 10 т/м3 = 1 кг/см2 = 1,03 * 105 Па
Пример 5.
В закрытом сосуде с водой давление на свободную поверхность (с
учетом атмосферного) равно Ро = 1,25 * 105 Па. На какую высоту поднимется вода в пьезометре, сообщающемся с сосудом на глубине h = 3 м под свободной поверхностью.
Решение:
Пьезометрическую высоту определим:
Ро + γ h = Ра + γ hр; hр = (Ро + γ h - Ра) / γ;
hр = (1,25 * 105 Па + 0,001 * 300 - 1,03 * 105 = 550 см = 5,5 м. (Ответ: hр = 5,5 м)
Пример 6.
В сосуде А часть воздуха выкачана и давление в нем Рраз = 0,6 * 105
Па. Сосуд А соединен трубкой с водой в сосуд В, свободная поверхность которой находится под давлением атмосферы. Определить высоту hб.
Решение: Высота водного столба в трубке определяется из уравнения:

hб = (Ра - Рраз) / γ,
где: Ра = 1 * 105 Па; Рраз = 0,6 * 105 Па;
γ = 0,004 кг/см2
Подставим эти величины в уравнение и получим:
hб = (1 * 105 Па - 0,6 * 105 Па) / 0,001 = 400 см = 4 м.
(Ответ: hб = 4 м.)
Пример 7.
Имеем два сообщающихся сосуда. В первый сосуд налита ртуть h1 =
0,1 м, а во втором сосуде – вода. Определить высоту столба воды hв во втором сосуде.
Решение:
Для ртути γ р = 13,6 т/м3, а д ля воды γ в = 1 т/ м3.
Следовательно: 0,1 / hв = 1,0 / 13,6;
hв = (13,6 * 0,1) / 1,0 = 1,36 м.
(Ответ: hв = 1,36 м.)
Пример 8.
Определить горизонтальную силу Рх, стремящуюся сдвинуть каменную плотину, если длина плотины ( ширина стены) в = 5 м и глубина перед плотиной h = 4 м.
Решение:
Сила давления воды на стенку плотины будет:
Р = γ hс * w, т.к. hс = h/m; w = в γ; γ = h/sin ;
Р = γ h2в/2 sin a,
где: – угол наклона откоса плотины к горизонту.
Горизонтальная проекция силы давления будет:

Рх = Р * cos (90 – )
Подставляя вместо Р его значение и заменяя cos (90 – ) = sin , получим:
Р = (γ h2 в sin )/2 = (1* 42 * 5)/2 = 40 т = 412 *107 Па
(Ответ: Р = 412 *107 Па)
Контрольные вопросы для самопроверки
1.Что называется гидравликой и на какие основные части она
делится?
2.В чем состоит производственное значение гидравлики?
3.Какова роль русских и российских ученых в развитии гидравлики?
4.Что называют объемным весом жидкости, от чего он зависит и какие его расчетные значения для пресной воды?
5, Что такое плотность жидкости, ее формулы?
6.Чем характеризуется сжимаемость жидкости?
7.Что такое вязкость жидкости и ее кинематический коэффициент?
8.Какие основные понятия давления: абсолютное, манометрическое,
вакуумометрическое, пьезометрическое?
9. Какие свойства гидростатического давления?
10. Написать основное уравнение гидростатики, объяснить входящие
внего величины и практическое применение?
11.Что такое пьезометрическая высота?
12.Как определяются силы гидростатического давления на плоскую
стенку?
1.2. Гидродинамика
Движение жидкости представляет собой сложное явление. Поэтому получить общий закон движения жидкости, отражающий все его особенности, трудно. Гидравлика решает вопросы движения жидкости следующим образом. На первом этапе решения проблемы используется
упрощенная модель – невязкая жидкость. Полученные для невязкой жидкости принципиальные решения корректируют с помощью экспериментальных данных. Гидравлика стремится в каждом конкретном случае выделить основные особенности движения жидкости. Отсюда многообразие определений: движение установившееся и неустановившееся,
равномерное и неравномерное, ламинарное и турбулентное, напорное и безнапорное, плавноизменяющееся и разноизменяющееся и т.д. Этим понятиям нужно уделить особое внимание и по каждому определению необходимо выполнить решение экспериментальных задач. Методов изучения движения жидкости известно всего лишь два:
1. Метод Л.Эйлера предусматривает периодическую фиксацию всех возможных характеристик движения жидкости в отдельных точках объема.
Метод Л.Эйлера в большей степени используется в гидравлике по изучению движения жидкости, то есть изучения гидродинамики.
Значительную роль в этом методе играет линия тока – линия, в которой в данный момент времени вектор скорости частиц направлен по касательной.
Это основа многих понятий и закономерностей гидродинамики.
2. Метод Легранта изучает гидродинамику, используя для решения поставленных задач постоянное наблюдение за движением отдельных частиц и на основе этого определяется характер и особенности движения жидкости на всем изучаемом объекте целиком.
1.2.1. Поток жидкости и его элементы.
Уравнение неразрывности движения основан на свойстве жидкости занимать определенный объем, строго соответствующий данному количеству жидкости, и практически не изменять этот объем под действием приложенных к жидкости сил. Элементы уравнения неразрывности следующие: расход или приток жидкости – Q, м3/с; средняя скорость движения жидкости – V, м/с; площадь живого сечения потока – w, м2 –

используются во всех разделах гидравлики и при расчете задач,
применяемых на практике.
Часто используются и две следующие геометрические характеристики живого сечения потока: смоченный периметр водотока или потока – Х, м; гидравлический радиус – R, м.
Для решения практических задач большое значение имеет уравнение Д. Бернулли, с помощью которого решаются задачи: при истечении жидкости из отверстий и через насадки, напорные водопропускные трубы,
движение жидкости в открытых руслах, через водосливы.
1.2.2. Уравнение Д. Бернулли
Уравнение Д.Бернулли – одно из основных уравнений гидравлеки.
Оно представляет собой частный случай закона сохранения энергии.
Z1 + P1 / γ + |
V2 |
1 /2g = Z2 + P2 / γ + V2 |
2 /2 g + hw , |
|
где: Z1 и Z2 |
- называются ординатами высот |
положения |
||
произвольно выбранных точек в сечениях потока над плоскостью сравнения;
P1 / γ и P2 / γ – пьезометрическая высота давления;
V2 1 /2g и V2 2 /2 g - потеря напора при движении потока от первого сечения до второго.
Для использования уравнения Д.Бернулли составляют применительно к единице веса жидкости, поэтому все виды энергии в этом уравнении выражаются линейными величинами. В первую очередь эти расчеты применяются к отверстиям и насадкам. Отверстие называется малым, если можно пренебречь изменениями по его площади. Насадком называется небольшая по длине трубка, присоединенная к такому отверстию. И
отверстия и насадки широко используются в гидротехнических сооружениях.
