Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежская государственная лесотехническая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1856

.pdf

Скачиваний:

Добавлен:

08.01.2021

Размер:

328.68 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ВОРОНЕЖСКАЯ ГОСУДАРСТВЕННАЯ ЛЕСОТЕХНИЧЕСКАЯ АКАДЕМИЯ

ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Методические указания к выполнению лабораторных работ

для студентов специальности 220301 – Автоматизация технологических процессов и произ-

водств в лесном комплексе Часть 2

ВОРОНЕЖ 2004

УДК 681.5

Петровский В.С. Теория автоматического управления: Методические указания к выполнению лабораторных работ для студентов специальности 220301

– Автоматизация технологических процессов и производств в лесном комплексе /В.С. Петровский, Д.А. Глухов; ВГЛТА.− Воронеж, 2004. – 35 с.

Печатается по решению редакционно-издательского совета ВГЛТА

Рецензент доктор техн. наук, профессор, зав. кафедрой АТП ВГАСУ В.Д.Волков

Ответственный редактор кандидат техн. наук,

доцент кафедры АПП ВГЛТА С.И. Поляков

Лабораторная работа №1 Исследование устойчивости и качества АСР, состоящей из объекта

1-го порядка и ПИ-регулятора Цель работы: провести анализ устойчивости системы, состоящей из

объекта, представляющего собой апериодическое звено 1-го порядка и ПИрегулятора.

Краткие теоретические сведения

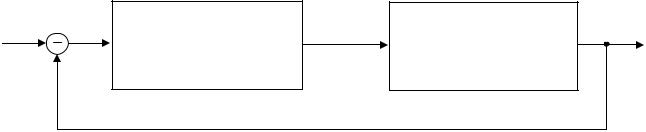
Структурная схема АСР представлена на рис.1.1.

G(t)	Wрег	(P)	Wоб (P) Y(t)

Рис.1.1 Структурная схема АСР

Передаточная функция регулятора

(P) = k

kрег

(1.1)

рег

Передаточная функция объекта

Wоб ( p) =

kоб

(1.2)

Tоб

P +1

где kрег ,kоб − коэффициенты усиления регулятора и объекта; Tоб − постоянная времени объекта;

tи − время изодрома;

P − параметр Лапласа, который при нулевых начальных условиях отожде-

ствляется с оператором дифференцирования						d		.
ствляется с оператором дифференцирования								.
						dt
Передаточная	функция		системы		в				разомкнутом		состоянии
Wраз (P) =Wрег (P) Wоб (P) , в замкнутом состоянии с отрицательной обрат-
ной связью
	W		(P) =	Wраз (P)			=		Y(P)	,	(1.3)
		зам
				1+Wраз (P)					G(P)

где Y(P) − изображение по Лапласу регулируемого параметра;

G(P) − изображение по Лапласу управляющего (задающего) воздействия системы регулирования.

Следовательно, дифференциальное уравнение АСР в операторной форме имеет вид

Y(P) (1+Wрег (P) Wоб (P)) = G(P) Wрег (P) Wоб (P).

(1.4)

Подставив в уравнение (1.4) передаточные функции объекта (1.2) и регулятора (1.1) и проведя необходимые преобразования с переходом к оригиналам функций y(t), g(t) , получим дифференциальное уравнение линейной системы автоматического регулирования

d2 y

+ (t

)

+ y = t

+ g.

(1.5)

об

dt2

об

рег

об

рег

Характеристическое уравнение имеет вид

1+W

рег

(P) W

(P) = A P2

+ A P + A ,

(1.6)

об

где

A =

Tоб tи

;

A = t

tи

;

A =1.

(1.7)

kоб kрег

kоб

k рег

Построим кривую переходного процесса, используя классический метод решения дифференциального уравнения (1.5) для скачкообразного управляющего воздействия g(t) =g01(t), (g0 = const) . Процесс регулирования опре-

деляется в виде

	y(t) = yуст (t) + yпер (t),	(1.8)
где	yуст (t) − установившаяся составляющая; yпер (t) − переходная составляю-
	n
щая;	yпер (t) = ∑Ck l Pk t , где Pk −корни характеристического уравнения (1.6);
	k =1

Ck − постоянные интегрирования, зависящие от начальных условий. Численные значения постоянных C1,C2 ,...,Cn находятся из реализации теоремы

о начальном значении оригинала функции и её производных и решения системы n − линейных алгебраических уравнений с n неизвестными

n
y(i) (t) = y(устi) (t) + ∑(Pk )i Ck	l Pk t ; i = 0,1,2,...,n −1.			(1.9)
k=1
Установившаяся составляющая
y (t)=t		dg	+g=1.	(1.10)
y (t)=t			+g=1.	(1.10)
уст	и dt

Так как характеристическое уравнение (1.6) имеет два корня, переходная составляющая имеет два члена

y	пер	(t) = C lP t1	+ C	2	lP2 t .	(1.11)
	пер	1		2

Подставив (1.10) и (1.11) в (1.8), получим кривую переходного процесса системы

y(t) =1+ C lP t1	+ C	2	lP2 t .	(1.12)
1		2

Постоянные интегрирования C1,C2										из уравнения (1.12) находятся из
системы, состоящей из двух уравнений и имеющей два неизвестных
					+ C1		lP t1		+ C2				lP2 t		= 0;
				1	+ C1				+ C2						= 0;							(1.13)
						P lP t11 + C						P lP t12 =										(1.13)
				C		P lP t11 + C					2	P lP t12 =					0.
					1	1					2			2
																					Таблица 1.1
	Варианты исходных данных

№	1	2	3	4		5		6		7				8		9		10	11	12	13	14	15
kоб	2,0	2,2	2,4	2,6		2,8		3,0		3,2				3,4		3,6		3,8	4,0	4,2	4,4	4,6	4,8
kоб
T	15	20	25	30		35		40		45				50		55		60	65	70	75	80	85
об

Порядок выполнения работы

1Задать исходные данные, присвоив переменным kрег ,tи ,kоб ,Tоб значения. kоб и Tоб определяются в соответствии с вариантом, предложенным преподавателем табл.1.1. kрег и tи задаётся из диапазона 0,1...60. Входная величина g = 1. Для этого необходимо:

•ввести в желаемом месте документа имя переменной;

•ввести оператор присваивания с помощью клавиши <:> или нажатием соответствующей кнопки Definition (Присваивание) на панели инструментов Calculator (Калькулятор) или Evaluation (Выражение);

•ввести в появившейся местозаполнитель значение переменной.

2Далее следует найти корни характеристического уравнения (1.6). Для этого необходимо вычислить коэффициенты A0 , A1, A2 по формулам

(1.7). Корни уравнения (1.6) определяются, используя встроенную функцию polyroots(v) , где v − вектор, составленный из коэффициентов характеристического уравнения. Возвращающим значением данной функции будет вектор, составленный из корней рассматриваемого уравнения рис.1.2.

Для построения вектора нужно, поставив курсор в местозаполнитель, с помощью клавиши <Ctrl>+<C> или нажатием соответствующей кнопки Matrix or Vector (Создание матрицы или вектора) на панели инструментов Matrix (Матрица) вызвать окно Insert Matrix (Вставить матрицу), где задать число столбцов (для вектора равно 1) и строк.

	A2
	A1		−0.15 − 0.421i
v :=	A1	p := polyroots (v) p =	−0.15 − 0.421i
		p := polyroots (v) p =	−0.15 + 0.421i
	A0

Рис.1.2 Нахождение корней характеристического уравнения

3Проанализировав полученные данные, составить уравнение, описывающие переходной процесс системы. Для этого следует воспользоваться теоретической частью данной работы.

4Задать временной интервал t , на котором будет производиться исследование. Рекомендуется использовать не менее 10 шагов в интервале. Для этого необходимо:

•ввести в желаемом месте документа имя переменной t ;

•нажать кнопку Range Variable (Ранжированная переменная) на панели Matrix (Матрица), либо ввести символ <;> с клавиатуры;

•в появившихся местозаполнителях ввести нижний и верхний

пределы изменения времени t . Чтобы задать шаг изменения переменной

•поместить линию ввода на значение начала диапазона;

•ввести запятую <,>;

•в появившийся местозаполнитель ввести значение шага измене-

ния переменной.

Пример задания временного интервала показан на рис.1.3.

t := 0,30.. 300

Рис.1.3 Интервал изменения времени

5Найти постоянные интегрирования C1 ,C2 . Они находятся из решения системы уравнений (1.13). Для решения системы уравнений (1.13) в среде MathCAD необходимо:

•в свободном месте документа написать ключевое слово “Given”;

•ниже записывается система с использованием логических опера-

торов равенства.

Логический оператор равенства следует вставлять пользуясь, панелью инструментов Boolean (Булевы операторы), либо сочетанием клавиш <Ctrl>+<=>.

•для решения системы относительно переменных C1 ,C2 используется встроенная функция Find , аргументами которой являются

искомые переменные.

Для нахождения решения системы в общем виде необходимо выделить курсором функцию Find и вставить оператор символьного вывода нажатием соответствующей кнопки на панели Symbolic (Символика) или Evaluation (Выражения), либо сочетанием клавиш <Ctrl>+<.>.

Пример решения системы уравнений показан на рис.1.4.

Given
1 + C ep1 t					+ C ep2 t					0


1					2
C p	1	ep1 t			+ C p		2	ep2 t				0
C p		ep1 t			+ C p			ep2 t				0
1					2
											p2

						(p		− p ) exp(p									t)
Find(C ,C						(p		− p ) exp(p									t)
Find(C ,C				) →			1			2						1
		1	2							−p1
							(		2	−p1				1				2)
							(		2		)	(		1				2)
						exp p				t			p		− p

Рис.1.4 Решение системы уравнений

Необходимо присвоить постоянным интегрирования C1 ,C2 их значения в общем виде, из полученного выше вектора столбца рис.1.5. Причём переменная t в этих выражениях равняется 0 .

C1 := p2	1	C2 := −p1	1

	(p1 − p2)		(p1 − p2)

Рис.1.5 Присвоение постоянным интегрирования полученных значений

6На данном шаге необходимо задать ранее составленное уравнение переходного процесса системы. Оно представляет собой функцию y(t) . Для этого нужно:

•ввести в желаемом месте документа имя функции y(t) ;

•в появившемся местозаполнителе ввести полученное ранее вы-

ражение, описывающее переходной процесс.

7Построить график, отложив по вертикальной оси выходную величину y(t) , а по горизонтальной – время t . Для построения графика нужно с

помощью клавиши <Shift>+<2> или нажатием соответствующей кноп-

ки XY Plot (XY (декартовый) график) на панели инструментов Graph (График) вывести шаблон графика, где по оси абсцисс задать время t , а по оси ординат выходную величину y(t) .

8Изменив значения kрег и tи , повторить расчёт. Количество расчётов задаётся преподавателем.

Содержание отчёта

•Название и цель лабораторной работы.

•Графики динамических характеристик.

•Выводы по каждому из графиков о качестве и устойчивости системы.

•Вывод о влиянии параметров регулятора на качество и устойчивость системы.

Лабораторная работа №2 Исследование устойчивости и качества АСР, состоящей из объекта

2-го порядка и ПИ-регулятора Цель работы: провести анализ устойчивости системы состоящей из

объекта, представляющего собой апериодическое звено 2-го порядка и ПИрегулятора.

Краткие теоретические сведения

Структурная схема АСР представлена на рис.2.1.

G(t)	Wрег	(P)	Wоб (P) Y(t)

Рис.2.1 Структурная схема АСР

Передаточная функция регулятора

(P) = k

kрег

(2.1)

рег

Передаточная функция объекта

Wоб ( p) =

kоб

(2.2)

(Tоб1

P +1)

(Tоб2 P +1)

где kрег ,kоб − коэффициенты усиления регулятора и объекта; Tоб1 ,Tоб2 − постоянные времени объекта;

tи − время изодрома;

P − параметр Лапласа, который при нулевых начальных условиях отожде-

ствляется с оператором дифференцирования						d	.
ствляется с оператором дифференцирования							.
					dt
Передаточная	функция	системы		в				разомкнутом		состоянии
Wраз (P) =Wрег (P) Wоб (P) , в замкнутом состоянии с отрицательной обрат-
ной связью
	W (P) =		Wраз (P)			=		Y(P)	,	(2.3)


	зам		1+Wраз	(P)				G(P)
			1+Wраз	(P)				G(P)

где Y(P) − изображение по Лапласу регулируемого параметра;

G(P) − изображение по Лапласу управляющего (задающего) воздействия системы регулирования.

Следовательно, дифференциальное уравнение АСР в операторной форме имеет вид

Y(P) (1+Wрег (P) Wоб (P)) = G(P) Wрег (P) Wоб (P).

(2.4)

Подставив в уравнение (2.4) передаточные функции объекта (2.2) и регулятора (2.1) и проведя необходимые преобразования с переходом к оригиналам функций y(t),g(t) , получим дифференциальное уравнение линейной системы автоматического регулирования.

Найдём общее и частное решение полученного дифференциального уравнения для скачкообразного управляющего воздействия g(t) =g01(t), (g0 = const) .

Характеристическое уравнение имеет

1+W

рег

(P) W

(P) = A P

3 + A P

2 + A P + A ,

(2.5)

об

где

To1

To2

A1 =

+ T

) t

A2 = ti +

A3 =1.

(2.6)

;

ko kr

Построим кривую переходного процесса, используя классический метод решения дифференциального уравнения для скачкообразного управляющего

воздействия g(t) =g01(t),		(g0 = const) . Процесс регулирования определяется в
виде
		y(t) = yуст (t) + yпер (t),	(2.7)
где	yуст (t) − установившаяся составляющая; yпер (t) − переходная составляю-
	n	где Pk −корни характеристического уравнения (2.5);
щая;	yпер (t) = ∑Ck l Pk t ,	где Pk −корни характеристического уравнения (2.5);

k =1

n
y(i) (t) = y(устi) (t) + ∑(Pk )i Ck lPk t ; i = 0,1,2,...,n−1.				(2.8)
k=1
Установившаяся составляющая
y (t)=t		dg	+g=1.	(2.9)
y (t)=t			+g=1.	(2.9)
уст	i dt

Так как характеристическое уравнение (2.5) имеет два корня, переходная составляющая имеет два члена

y	пер	(t) = C lP t1	+ C	2	lP2 t + C	3	lP3 t .	(2.10)
	пер	1		2		3

Подставив (2.9) и (2.10) в (2.7) получим кривую переходного процесса системы

				y(t) =1+C lP t1									+C				2	lP2 t +C lP3 t .								(2.11)
							1										2				3
Постоянные интегрирования C1 ,C2,C3 из уравнения (2.11) находятся из
системы, состоящей из двух уравнений и имеющей два неизвестных
					+C1		lP1 t		+C2					lP2		t		+ C3		lP3	t	= 0;
				1	+C1				+C2									+ C3				= 0;
						P lP1 t +C						P				lP2 t			+ C		P lP3 t = 0;					(2.12)
				C		P lP1 t +C					2	P				lP2 t			+ C		P lP3 t = 0;					(2.12)
					1	1					2				2					3		3
				C P21 lP1 t + C									2		P 2 lP2 t + C P2								lP3 t = 0.
					1								2			2						3 3
																									Таблица 2.1
	Варианты исходных данных

№	1	2	3	4		5		6		7						8			9			10	11	12	13	14	15
kоб	2,0	2,2	2,4	2,6		2,8		3,0		3,2						3,4			3,6			3,8	4,0	4,2	4,4	4,6	4,8
kоб
Tоб1	15	20	25	30		35		40		45						50			55			60	65	70	75	80	85
Tоб2	75	70	65	60		55		50		45						40			35			30	25	20	15	10	5

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.01.2021328.25 Кб41851.pdf
#
08.01.2021328.29 Кб11852.pdf
#
08.01.2021328.49 Кб21853.pdf
#
08.01.2021328.51 Кб21854.pdf
#
08.01.2021328.54 Кб01855.pdf
#
08.01.2021328.68 Кб01856.pdf
#
08.01.2021328.73 Кб11857.pdf
#
08.01.2021328.75 Кб21858.pdf
#
08.01.2021328.83 Кб01859.pdf
#
08.01.2021169.21 Кб0186.pdf
#
08.01.2021328.84 Кб11860.pdf