
1568
.pdfМинистерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный лесотехнический университет им. Г.Ф. Морозова»
ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Методические указания к лабораторным работам для студентов
по направлению подготовки 35.03.02 – Технология лесозаготовительных и деревоперерабатывающих производств;
Профиль: Технология мебели, материалов и изделий из древесины
Воронеж, 2016
УДК 658.5.011.56
Поляков, С. И. Теория автоматического управления [Текст]: метод. указания к лабораторным работам для студентов по направлению подготовки 35.03.02
– Технология лесозаготовительных и деревоперерабатывающих производств;
Профиль: Технология мебели, материалов и изделий из древесины/ С. И.
Поляков; Мин-во обр-я и науки Рос. Фед., ФГБОУ ВО «ВГЛТУ». – Воронеж,
2016. 16 с.
Печатается по решению редакционно-издательского совета ФГБОУ ВО «ВГЛТУ»
Рецензент: профессор кафедры автоматизации технологических процессов и производств Воронежского государственного архитектурно-
строительного университета В.И. Акимов
2

Введение При создании высококачественных систем автоматического
управления необходимым условием является их устойчивость. Для того,
чтобы система была устойчивой, то есть ее реакция была бы ограниченной при ограниченном входном воздействии, необходимо и достаточно, чтобы временная характеристика g(t) системы была бы абсолютно интегрируемой
|
|
||||
|
|
g( ) |
|
d |
(1) |
|
|
||||
0 |
|
|
|
|
|
Докажем это: пусть внешнее воздействие x(t)<M0; t>0, значит и
X(t- ) ; (t );
Известно, что реакция системы y(t) связана с x(t) следующим образом
t
y(t) g( )x(t )d
0
Оценим абсолютную величину реакции y(t)
t
y(t) g( )
 x(t ) d
x(t ) d
0
Учитывая (2) и увеличивая верхний предел интегрирования до бесконечности, что усиливает неравенство, получим
y(t) M 0 g(t) d
0
(2)
(3)
(4)
Из выражения (4) следует, что реакция системы будет ограниченной,
если интеграл от абсолютного значения временной характеристики конечен,
что и требовалось доказать.
При анализе и синтезе САУ выражение временной характеристики может иметь сложный вид и нахождение значения интеграла (1) становится затруднительным.
3
Существуют более простые способы оценки устойчивости систем с помощью критериев. Критерии устойчивости делятся на два больших класса:
корневые или алгебраические и частотные.
Задание
1.Получить у преподавателя исходные данные для выполнения лабораторной работы.
2.Проверить устойчивость линейной САУ, используя критерий Рауса и критерий Гурвица.
3.Проверить устойчивость линейной САУ, используя частотные критерии:
критерий Михайлова и критерий Найквиста.
4.Построить логарифмические частотные характеристики линейной разомкнутой системы и найти запасы устойчивости по фазе и амплитуде.
5.Рассчитать параметры линейной системы, при которых она выходит на границу устойчивости.
6.Проверить устойчивость нелинейной САУ методом Попова. Проверить наличие автоколебаний в нелинейной системе.
7.Сделать выводы.
Исходные данные
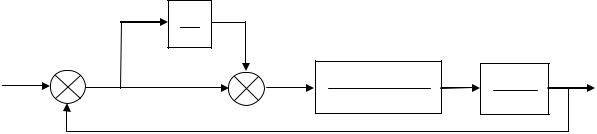
Дана структурная схема:
K1
P
K2
T12 P2 T3P 1
K4
T4 P 1
Рис. 1
4
Значения параметров коэффициентов передаточных функций:
K1 3
K2 2
K3 7
K4 2.8
T1 1.5 10 2
T2 0.05
T3 6 10 2
T4 0.13
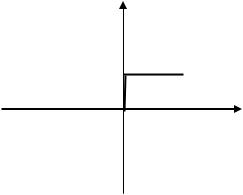
Вид нелинейности (Рис. 2):
15
 -15
-15
Рис. 2
Алгебраические критерии
Для того, чтобы система автоматического управления была устойчивой,
необходимо и достаточно, чтобы все корни еѐ характеристического уравнения (знаменателя передаточной функции) были бы левыми на комплексной плоскости, т.е. имели бы отрицательные действительные части.
Характеристическое уравнение имеет вид:
a( p) a0 pn a1 pn 1 .. an 1 p an ,
где a0,..,an - коэффициенты, p - параметры.
5
Из исходных данных видно, что передаточные функции отдельных
звеньев имеют вид:
W ( p) |
|
K1 |
; |
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
1 |
|
|
|
P |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
W2 |
( p) |
|
|
|
K 2 |
|
; |
||||
T |
2 P 2 |
T P 1 |
|||||||||
|
|
|
|
|
|||||||
|
1 |
|
3 |
|
|
||||||
W3 |
( p) |
|
|
K 4 |
|
; |
|
|
|||
|
|
|
|
|
|
||||||
|
|
|
T4 P 1 |
|
|||||||
Зная, передаточные функции отдельных звеньев можно найти |
|||||||||||
передаточную функцию разомкнутой системы: |
|||||||||||
Wраз(p)= W1(p) 1 W2(p) W3(p)= |
|
|
K1 p K2 K4 |
|
|
|||
T |
T 2 p4 |
p3(T T T 2 ) p2(T T ) p |
||||||
|
||||||||
4 |
1 |
3 |
4 |
1 |
3 |
4 |
||
Теперь найдем передаточную функцию замкнутой системы, используя
структурную схему и приведя подобные слагаемые, получим:
Wзам(p)= |
|
Wзам ( p) |
= |
|
|
|
|
K1 |
p K2 |
K4 |
|
|
|
|
|
|
|
|
|
|||
|
W |
|
( p) |
T |
T 2 p4 |
p3(T T T 2 ) p2(T T ) p(K |
|
K |
|
1) K |
|
K |
|
K |
|
|||||||
1 |
зам |
|
2 |
4 |
1 |
2 |
4 |
|||||||||||||||
|
|
|
|
4 |
1 |
3 |
4 |
1 |
3 |
4 |
|
|
|
|
|
|||||||
Значит, искомое характеристическое уравнение системы примет вид:
Q(p)=T4 T12 p4 p3(T3 T4 T12 ) p2(T3 T4 ) p(K2 K4 1) K1 K2 K4
Коэффициенты в характеристическом уравнении будут равны:
A0 2.925 10 5
A1 8.025 10 3
A2 0.19
A3 6.6
A4 16.8
А5=0
Критерий Рауса
6

Для того, чтобы система была устойчивой, необходимо и достаточно,
чтобы все коэффициенты первого столбца таблицы Рауса были положительными.
Если хотя бы один из коэффициентов характеристического уравнения отрицателен, то система неустойчива; если хотя бы один из коэффициентов равен нулю, то система находится на грани устойчивости.
Составим таблицу Рауса, но прежде найдем недостающие коэффициенты:
B0 |
A1 |
A3 |
B0 |
1.332 10 3 |
A0 |
A2 |
B2 |
A1 |
A5 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
B1 7.707 |
|
|
|
|
|
|
|
|
||||
|
|
A0 |
A4 |
|
|
10 |
|
|
|
|
|
|
|
|
||||
B1 |
|
B0 |
B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A1 |
A3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
B2 0.135 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Тогда таблица Рауса примет вид: |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2.925 |
10 5 |
0.19 16.8 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
8.025 |
10 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
6.6 |
0 |
|
|
||
|
|
1 |
a0 |
a2 |
a4 |
|
RAUSA |
|
3.645 10 3 |
0.166 |
16.8 |
0 |
|
|
||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
a1 |
a3 |
a5 |
|
|
|
0.048 |
5.788 |
0 |
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
c31 |
c32 |
или |
|
|
0.029 |
0 |
|
0 |
0 |
|
|
||||
|
|
|
c33 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
c41 |
c42 |
c43 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
3 |
c51 |
c52 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
c53 |
|
|
|
|
|
|
|
|
|
|
|||||
Видно, что все коэффициенты в первом столбце таблицы Рауса положительны, но они также довольно близки к нулю, значит по этому критерию система близка к грани устойчивости.
Критерий Гурвица
7

Для того, чтобы система была устойчивой, необходимо и достаточно,
чтобы при а0>0 все определители матрицы Гурвица были бы положительны.
Составим матрицу Гурвица:
a1 |
a3 |
a5 |
a7 |
|
|||
|
|
|
|
|
|
|
|
a0 |
a2 |
a4 |
a6 |
|
|||
|
0 |
a |
a |
|
a |
|
|
|
|
1 |
|
3 |
|
5 |
|
|
0 |
a0 |
a2 |
a4 |
|||
Теперь найдем определители Гурвица:
A1 8.025 10 3 

A1 |
A3 |
|
|
|
|
|
3 |
|
|||||
A0 |
A2 |
|
1.332 10 |
|
|
|
|
||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
A1 |
A3 |
|
|
0 |
|
7.707 10 3 |
|
||||||
A0 |
A2 |
|
A4 |
|
|
|
|||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
A1 |
|
A3 |
|
|
|
|
|
|
|
||
A1 |
A3 |
|
0 |
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
||||||||
A0 |
A2 |
A4 |
0 |
0.129 |
|
|
|
|
|||||
|
0 |
A1 |
A3 |
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
A0 |
A2 |
A4 |
|
|
|
|
|
||||
Видно, что все главные определители в матрице Гурвица положительны, значит по этому критерию система устойчива.
Частотные критерии Частотные критерии базируются на частотных характеристиках,
которые легко получить экспериментально, либо рассчитать теоретически.
8

А) Критерий А. В. Михайлова |
|
|
|
|
|
|
|
||
Рассмотрим характеристический |
полином |
|
и заменим |
р на jw (w - |
|||||
частота) |
|
|
|
|
|
|
|
|
|
a( j) a |
( j)n a ( j)n 1 |
a |
n 1 |
( j) a |
0 |
U ( ) jV ( ), |
|||
0 |
1 |
|
|
|
|
|
|
||
где U(w)-действительная часть частотной характеристики, V(w) - |
|||||||||
мнимая часть. a(jw) |
изобразим |
в |
виде |
кривой на |
комплексной |
||||
плоскости, которая называется годографом Михайлова. |
|
||||||||
Система устойчива, если годограф Михайлова при увеличении w от нуля
до бесконечности начинается на действительной положительной полуоси,
огибает против часовой стрелки начало координат, проходя последовательно n квадрантов (n – порядок системы).
В нашем случае система имеет следующее характеристическое
уравнение:
a(j )=T4 T12 j 4 j 3 (T3 T4 |
T12 ) j 2 (T3 T4 |
) j(K2 |
K4 1) K1 |
K2 K4 |
|||||||||||||||||||||||||
200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
800 |
|
600 |
|
|
400 |
200 |
0 |
200 |
400 |
||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im(Q(w)) |
|
|
|
|
|
|
|
|
|
|
|
|
2000 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4000
4500
800 |
Re(Q(w)) |
400 |
Рис. 3
9
Итак, годограф пересекает четыре квадранта, значит наша система
устойчива.
Б) Критерий Найквиста Критерий позволяет судить об устойчивости замкнутой системы по
амплитудно-фазовой частотной характеристике разомкнутой системы.
Построить АФХ разомкнутой системы значительно проще но сравнению с замкнутой.
Известно, что при последовательных и параллельных соединениях устойчивых звеньев получается устойчивая система, и наоборот, если хотя бы одно звено будет неустойчивым, система также становится неустойчивой.
Иное для замкнутых систем. В этом случае могут быть различные
варианты.
Рассмотрим систему с жесткой обратной связью. Это не ограничивает общности рассмотрения, так как используя алгебру передаточных функций,
систему с гибкой обратной связью можно преобразовать к системе с
жесткой обратной связью.
x |
|
|
y |
|
W(p) |
||||
|
|
|
||
|
|
|
|
|
|
|
|
|
Рис. 4
1.Разомкнутая система устойчива
Вэтом случае необходимо и достаточно, чтобы ЛФХ разомкнутой системы
не охватывала точку (-1, j0). ЛФХ разомкнутой системы получается из передаточной функции системы W(p) заменой р на jw АФХ строят при изменении частоты w от нуля до бесконечности.
2.Разомкнутая система неустойчива
То есть передаточная функция имеет К полюсов характеристическою уравнения в правой полуплоскости и не имеет их на мнимой оси. Для устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ
10
