Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежская государственная лесотехническая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1474

.pdf

Скачиваний:

Добавлен:

08.01.2021

Размер:

293.12 Кб

Скачать

☆

<<< < Предыдущая 12 / 22

Для симметричных распределений m3 = 0 и g1 = 0 . Для нормального распределения m4 / m22 = 3 .

Для удобства сравнения эмпирического распределения и нормального в качестве показателя эксцесса принимают величину:

		g2		= m4 / m22			−3	(1.26)
Несмещенные оценки для показателей асимметрии и эксцесса
определяют по формулам:
		G1	=		n(n −1)		g1 ,	(1.27)
		G1	=		n −2		g1 ,	(1.27)
					n −2
G2	=		n −1			[(n +1)g1 +6] .		(1.28)
G2	=	(n	−2)(n −3)			[(n +1)g1 +6] .		(1.28)
		(n	−2)(n −3)

Для проверки гипотезы нормальности распределения следует также вычислить среднеквадратические отклонения для показателей асимметрии и эксцесса:

SG	=		6n(n −1)		,			(1.29)
SG	=		(n −2)(n +1)(n	+3)	,			(1.29)
1			(n −2)(n +1)(n	+3)
1
SG2 =			24n(n −1)	2			.	(1.30)
SG2 =		(n −3)(n −2)(n +		3)(n +		5)	.	(1.30)
		(n −3)(n −2)(n +		3)(n +		5)

Если выполняются условия:


G1		≤ 3SG1	(1.31)
			(1.31)
			(1.32)
	G2	≤ 5SG2

то гипотеза нормальности исследуемого распределения может быть принята. Рассмотрим методику проверки гипотезы нормальности распределения

по X2 - критерию. Применение критерия X2 предполагает также использование свойств так называемого стандартного нормального распределения. Уравнение кривой стандартного нормального распределения имеет вид:

	1	e−	z2	≈ 0,4e−	z2
y = f (z) =						,	(1.33)
			2		2
	2π

где z = (x − μ) / σ .

Расчеты выполняют в табличной форме. Значения X2 вычислены по формуле:

X 2 = ∑(B − E)2 / E	(1.34)
(всех классов)

Данные таблицы можно использовать и для проверки гипотезы нормальности распределения с помощью критерия согласия КолмогороваСмирнова (К-С-критерия) ; для этого вычисляют:

D) = max FB − FE n

где FB — накопленная наблюдаемая частота; FE ожидаемая частота.

Процедура вычисления критерия х2

(1.35)

—накопленная Таблица 1.1

класса№

Середины интервалов

ВЧастоты

х2

Вх

Вх2

x − x

= z

Ординаты таблизf(z).

f (z)k '

B − E

(B − E)2

(B − E) 2

∑

x = ∑Bx / n ;

∑Bx2

−∑(Bx)2 / n

b - размер класса.

= nb / S ;

S =

;

n −1

Алгоритм предварительной обработки экспериментальных данных

При объеме выборки, превышающем 100—150 наблюдений, оптимальные эмпирические зависимости, отвечающие современному уровню знаний, можно построить только с помощью ЭВМ. Поэтому целесообразно включить в программу машинной обработки наблюдений также и предварительную обработку экспериментальных данных. Ниже дан алгоритм предварительной обработки наблюдений.

1.Вычисление выборочных характеристик x , S2, S, S , m1, m2, m3, m4 и

υ соответственно по следующим формулам:

∑n

x =

i=1

; S 2 = m2 =

∑(xi − x)2 ;

i=1

S =

∑n

(xi − x)2 ;

∑n

(xi − x)2 ;

n i=1

n −1 i=1

∑n

(xi − x) ; m2

∑n

(xi − x)2 ;

i=1

∑n

(xi − x)4 ; υ =

n i=1

2.Отсев грубых погрешностей: а) вычисляют наибольшее отклонение:

б) вычисляют τ = dmax /

;

dmax

xmax(min) − x

;

в) находят процентные точки

t-распределения Стьюдента t(p;n-2) , а

именно: t(5%;n-2) и t(0,1%;n-2).

г) вычисляют соответствующие точки τ(p,n) :

τ(5%;n)

t(5%;n−2)

n −1

(n −2) +

t(5%;n−2)

τ(0,1%;n)

t(0,1%;n−2)

n −1

(n −2) +

[t(0,1%;n−2) ]2

д) сравнивают результаты вычислений по п. 2б) и 2г); принимают окончательное решение об отсеве первой грубой погрешности, если результат по п. 2б) значительно больше результатов по п. 2г); _

е) пересчитывают выборочные характеристики x и S для нового массива данных (без отсеянного значения xi) при объеме массива п - 1;

ж) повторяют процедуру от п. 2а) до п. 2д) для следующего по абсолютной величине наибольшего отклонения dmax.

3.Проверка нормальности распределения (проводят только при

υ <33 %) : а) вычисляют g1 и g2 по формулам:

g1 = m3 / m23 / 2 ; g2 = m4 / m22 / 2 −3

б) находят несмещенные оценки для показателей асимметрии и эксцесса:

G1 =

(n −1)

g1 ; G2 =

n −1

[(n +1)g2 +6] ;

n −2

(n −2)(n −3)

в) определяют среднеквадратические отклонения:

6n(n −1)

24n(n −1)2

(n −2)(n +1)(n +3)

;

(n −3)(n −2)(n +3)(n +5)

г) проверяют условия

≤ 3SG1

, и

≤ 5SG2

(соблюдение этих условий

говорит о возможности принятия гипотезы нормального распределения) ; д) разбивают массив исходных данных на классы: k =1 +3,32 lg n ; е) определяют середины классов х; ж) подсчитывают частоты для всех классов В;

з) вычисляют для всех классов Вх и Вх2; и) находят x и S :

∑Bx

∑Bx2

−(∑Bx)2 / n

x =

, S =

;

n −1

к) вычисляют k ' = nb /

;

л) определяют z = (x − x) /

м) формируют вектор-столбец f(z);

н) вычисляют для всех классов E = f (z) ,

B − E , (B − E)2 ;

о) вычисляют X2 по формуле:

X 2 = ∑(B − E)2 / E ;

п) проверяют условие X 2 < X (2v; p) , v = nкл −1 −2 ;

p=0,10 (если это условие соблюдается, то гипотеза нормальности распределения может быть принята на 10 %-ном уровне);

р) вычисляют накопленные частоты FB и FE, используя частоты В и Е; с) находят:

D = max	FB − FE	;
)

	n

т) проверяют условие D < D(таблn;0,10) (если это условие соблюдается, то гипотеза нормальности распределения может быть принята на 10 %-ном уровне).

2. Метод наименьших квадратов в простейшем случае двумерного пространства (на плоскости).

Уравнение регрессии

К парным зависимостям типа у = f(x) относится подавляющее большинство всех формул, используемых в естественно-научных и технических дисциплинах. По результатам экспериментов такие формулы обычно строили, применяя метод наименьших квадратов, однако в последнее время с применением ЭВМ, пригодных для выполнения расчетов очень большого объема, удается построить парные зависимости оптимальной формы.

Процедура линейного парного регрессионного анализа (метода наименьших квадратов на плоскости) очень проста, и для ее выполнения достаточно настольной ЭВМ. (Эту процедуру можно выполнять и вручную). Большие ЭВМ требуются только для поиска оптимальной формы парной зависимости.

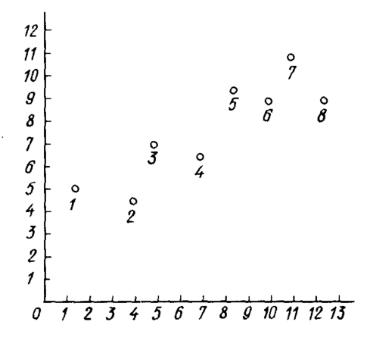
Пусть имеется п пар наблюдений значений функции отклика уi , полученных при фиксированных (в смысле записанных) значениях независимой переменной фактора xi . Для графического изображения этих пар наблюдений в виде экспериментальных точек с координатами х; у на плоскости применяется система декартовых координат (рис. 2).

Рисунок 2 - Графического изображения пар наблюдений в виде экспериментальных точек

Координаты точек 1—8, изображенных на рис. 2, приведены в табл. 2.1. Такие результаты наблюдений могут быть получены в любой экспериментальной работе.

						Координаты точек					Таблица 2.1
						Координаты точек
		1		2	3		4	5	6	7		8
х		1,5		4,0	5,0		7,0	8,5	10,0	11,0		12,5
у		5,0		4,5	7,0		6,5	9,5	9,0	11,0		9,0
	Задача		линейного		регрессионного			анализа	(метода		наименьших

квадратов) состоит в том, чтобы, зная положение точек 1—8 на плоскости, так провести линию регрессии, чтобы сумма квадратов отклонений 2i вдоль оси Оу

(ординаты) этих точек U от проведенной прямой была минимальной.

Для проведения вычислений по классическому методу наименьших квадратов (для проведения регрессионного анализа) к выдвигаемой гипотезе (к форме уравнения регрессии) предъявляется такое требование: это уравнение должно быть линейным по параметрам или допускать возможность линеаризации. Так, например, процедура проведения регрессионного анализа одинакова для уравнений y = b0 +bx и y = b0 +bz 2 , так как подстановка х = z2

приводит второе уравнение к первому. Предположим (на первых порах), что при проведении парного линейного регрессионного анализа имеем дело только с уравнением прямой линии (следует помнить, что это допущение делается только для упрощения усвоения начальных элементарных сведений по методике построения формул по опытным данным).

Уравнение прямой на плоскости в декартовых координатах

y = b0 +b1 x ,

(2.1)

где b0 , b1 — постоянные числа, геометрическая интерпретация которых дана ниже. Учитывая это, задачу метода наименьших квадратов аналитически можно выразить следующим образом:

U = ∑n [yi		−(b0	+b1 xi) ]min2
	i=1
yi −(b0	+b1 xi ) =		i , или
n
U = ∑	2
	2	i =1, n
	imin ,	i =1, n
i=1

(2.2)

(2.3)

Формулы (2.2) и (2.3) словами кратко можно выразить так: сумма квадратов отклонений вдоль оси Оу должна быть минимальной (принцип Лежандра).

Построенная таким образом линия регрессии позволяет в данном случае с некоторой вероятностью предсказать в интервале от х = 1,5 до х = 12,5 любые значения функции у при отсутствующих в табл. 2.1 значениях фактора х.

Для решения задачи, поставленной в формуле (2.2), необходимо в каждом конкретном случае вычислить значения коэффициентов b0 и b1, минимизирующие сумму отклонений U. Для этого, как известно из математического анализа, необходимо вычислить частные производные функции U по коэффициентам b0 и b1, и приравнять их нулю:

∂U∂b0∂U

∂b1

= 0,

(2.4)

= 0

Решая эту систему уравнений, находим искомые значения b0 и b1. Систему (2.4) называют системой нормальных уравнений. В формулу (2.4) подставляют значение U из формулы (2.2) и одновременно выполняют операцию дифференцирования:

∂U∂b0∂U∂b1

= ∑n [yi −(b0 +b1 xi )]= 0,

	i=1	(2.5)
	= ∑n	(2.5)
	= ∑n	[yi −(b0 +b1 xi )]xi = 0
	i=1

Преобразуем полученную систему нормальных уравнений:

b0 n +b1 ∑xi = ∑yi ,
b0 ∑xi +b1 ∑xi2 = ∑( yi xi )	(2.6)

В формуле (2.6) и далее для краткости у знака суммы ∑ опущены индексы. Систему (2.6) решаем с помощью определителей:

b0 = Θ1 / Θ , b1 = Θ2 / Θ

(2.7)

где Θ – главный определитель. Имеем:

Θ =	n	∑x	2	−(∑x)	2	(2.8)
	∑x	∑x2	= n∑x

Θ1	=	∑y		∑x	2	−∑xy∑x	(2.9)
		∑xy		∑x2	= ∑y∑x

Θ2	=		n	∑y	= n∑xy −∑x∑y		(2.10)

			∑x	∑xy

откуда


b0	=	∑y∑x2		−∑xy∑x	(2.11)
			n∑x2	−(∑x)2

	b1	=	n∑xy −∑x∑y		(2.12)
			n∑x2	−(∑x)2

Как и другие статистические расчеты, вычисление коэффициентов регрессии удобно проводить в табличной форме. На примере построения линии регрессии по данным табл. 2.1 можно рассмотреть практическую методику вычисления коэффициентов регрессии, которая приведена в табл. 2.2.

		Методика вычисления коэффициентов регрессии							Таблица 2.2
		Методика вычисления коэффициентов регрессии
п/п	х		х2	у		у2	ху	х+у		(х+у)2
1	2		3	4		5	6	7		8
1	1,5		5,0	2,25		25,0	7,50	6,50		42,25
2	4,0		4,5	16,00		20,25	18,00	8,50		72,25
3	5,0		7,0	25,00		49,00	35,00	12,00		144,00
4	7,0		6,5	49,00		42,25	42,50	13,50		182,25
5	8,5		9,5	72,25		90,25	80,75	18,00		324,00
6	10,0		9,0	100,00		81,00	90,00	19,00		361,00
7	11,0		11,0	121,00		121,00	121,00	22,00		484,00
8	12,5		9,0	156,25		81,00	112,50	21,5		462,25
∑	59,5		61,5	541,75		509,25	510,25	121,00		2072,00
				x = 7,4375	, y = 7,6875

					18

Для проверки правильности вычислений в табл. 2.2 можно использовать выражение:

∑(xi + yi )2 = ∑xi2 +2∑xi yi +∑yi2

(2.13)

Значения сумм подставляем в формулу (2.13). Получаем 2072,00 = 541,75+ + 2·510,25 + 509,75; 2072,00 = 2072,00. Следовательно, вычисления выполнены правильно. В формулу (2.11) и формулу (2.12) подставляем найденные значения для сумм из табл. 2.2, в результате получаем:

b0 = (61,50 541,75 −510,25 59,50) /(8 541,75 −3540,25) = 3,73 , b1 = (8 510,25 −59,50 61,50) /(8 541,75 −3540,25) = 0,53.

Уравнение регрессии или формула, которая отображает с некоторой вероятностью зависимость у от х , построенная по экспериментальным точкам, изображенным на рис. 4, имеет вид:

y = 3,73 + 0,53x

(2.14)

Это пример парной линейной зависимости.

3. Задание

Магистру, по выданным преподавателем (или определенным самостоятельно на практическом занятии) экспериментальным данным необходимо вычислить характеристики эмпирических распределений, моменты, произвести отсев грубых погрешностей, проверить нормальность распределения и методом наименьших квадратов построить уравнение регрессии.

Владимир Петрович Белокуров Геннадий Александрович Денисов Юрий Вячеславович Струков Наталья Ивановна Злобина

МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Методические указания для практических занятий для магистров направления подготовки 190700.68 – Технология транспортных процессов

Редактор

Подписано в печать	. Формат 60х90 / 16. Заказ
Объем п.л. Усл. печ. л.	. Уч.-изд. л. . Тираж экз.

ФГБОУ ВПО «Воронежская государственная лесотехническая академия» РИО ФГБОУ ВПО «ВГЛТА». 394087, г. Воронеж, ул. Тимирязева, 8 Отпечатано в УОП ФГБОУ ВПО «ВГЛТА»

<<< < Предыдущая 12 / 22

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.01.2021162.14 Кб2147.pdf
#
08.01.2021292.92 Кб11470.pdf
#
08.01.2021292.98 Кб11471.pdf
#
08.01.2021293.06 Кб11472.pdf
#
08.01.2021293.06 Кб11473.pdf
#
08.01.2021293.12 Кб21474.pdf
#
08.01.2021293.27 Кб01475.pdf
#
08.01.2021293.34 Кб01476.pdf
#
08.01.2021293.51 Кб21477.pdf
#
08.01.2021293.55 Кб01478.pdf
#
08.01.2021293.94 Кб31479.pdf