2426

qn9

qn9Н

x1, УЛЕ

z1, УЛЕ

Рис. 4.39. Зависимость диапазонных qn9B, qn9Н и оптимального qn9 значений управляемой координаты q9 в начальной точке положения груза от положений базового шасси q1, q3 (серия экспериментов № 1)

qk9

Рис. 4.40. Зависимость диапазонных qk9B, qk9Н и оптимального qk9 значений управляемой координаты q9 в конечной точке положения груза от положений базового шасси q1, q3 (серия экспериментов № 1)

260

qn10B, qn10Н, qn10, УЛЕ

qn10B

qn10

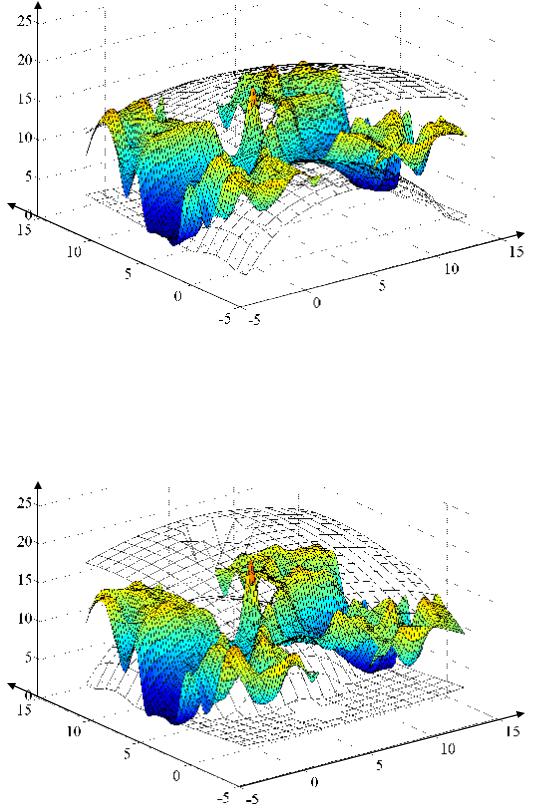
Рис. 4.41. Зависимость диапазонных qn10B, qn10Н и оптимального qn10 значений управляемой координаты q10 в начальной точке положения груза от положений базового шасси q1, q3 (серия экспериментов № 1)

qk10B, qk10Н, qk10, УЛЕ

qk10B

Рис. 4.42. Зависимость диапазонных qk10B, qk10Н и оптимального qk10 значений управляемой координаты q10 в конечной точке положения груза от положений базового шасси q1, q3 (серия экспериментов № 1)

261

Точки условного глобального минимума на рассматриваемой области, T=4,3 с

T, c

z1, УЛЕ

№ 1 № 2

x1, УЛЕ

Рис. 4.43. Зависимость временного критерия эффективности T от положений базового шасси q1, q3 при отсутствии ограничений на предельную линейную скорость груза (серия экспериментов № 1)

Реализация траектории с минимальным временем перемещения при оптимальном сочетании значений всех варьируемых параметров приводит к значительным колебаниям и раскачиванию груза под действием сил и моментов инерции (T=4,3 с), что было подтверждено при имитационном моделировании на математической модели динамической системы. Для ГПК с гибким подвесом груза реализация подобных траекторий практически неприменима по соображениям безопасности [170]. Поэтому в последующих сериях экспериментов учитывались рациональные ограничения на скорости изменения обобщенных координат ГПК, задаваемые человеком-оператором и аппроксимированные регрессионными выражениями вида (4.127), (4.133) и (4.138).

Данное ограничение обычно приближенно соблюдается челове- ком-оператором при ручном режиме управления ГПК. Человекоператор при этом руководствуется своим опытом и навыками. Использование комплекса разработанных методик в САУ СГК позволит более точно рассчитывать допустимую скорость движения звеньев, исключить ошибки, связанные с человеческим фактором, более полно использовать ресурс и технологические возможности машины.

Результаты 2-й серии экспериментов. В данной серии экспери-

ментов, в отличие от 1-й серии, учитывались ограничения по максимальным рациональным скоростям изменения управляемых коорди-

262

нат ГПК вида (4.127), (4.133) и (4.138). Препятствия в рабочей области отсутствовали [YПР(i,k)=0 (i,k)]. В качестве критерия эффективности также использовалось значение минимального времени перемещения T.

T, с

Точка минимума № 1, T=18,7 с

qn10, qn9, qn8, рад

qk8, qk9, qk10, рад

Рис. 4.44. Зависимость временного критерия эффективности T от начального и конечного значений управляемых координат q8, q9, q10 при постоянных координатах базового шасси (УЛЕ): q1= –1; q3= –3 (серия экспериментов № 2)

T, с

Точка минимума № 2, T=17,9 с

qn10, qn9, qn8, рад

qk8, qk9, qk10, рад

Рис. 4.45. Зависимость временного критерия эффективности T от начального и конечного значений управляемых координат q8, q9, q10 при постоянных координатах базового шасси (УЛЕ): q1= –3; q3= –3 (серия экспериментов № 2)

263

qn8B, qn8Н, qn8, рад

qn8B

qn8

z1, УЛЕ

qn8Н

x1, УЛЕ

Рис. 4.46. Зависимость диапазонных qn8B, qn8Н и оптимального qn8 значений управляемой координаты q8 в начальной точке положения груза от положений базового шасси q1, q3 (серия экспериментов № 2)

qk8B, qk8Н, qk8, рад

qk8B

qk8

qk8Н

Рис. 4.47. Зависимость диапазонных qk8B, qk8Н и оптимального qk8 значений управляемой координаты q8 в конечной точке положения груза от положений базового шасси q1, q3 (серия экспериментов № 2)

264

qn9

qn9Н

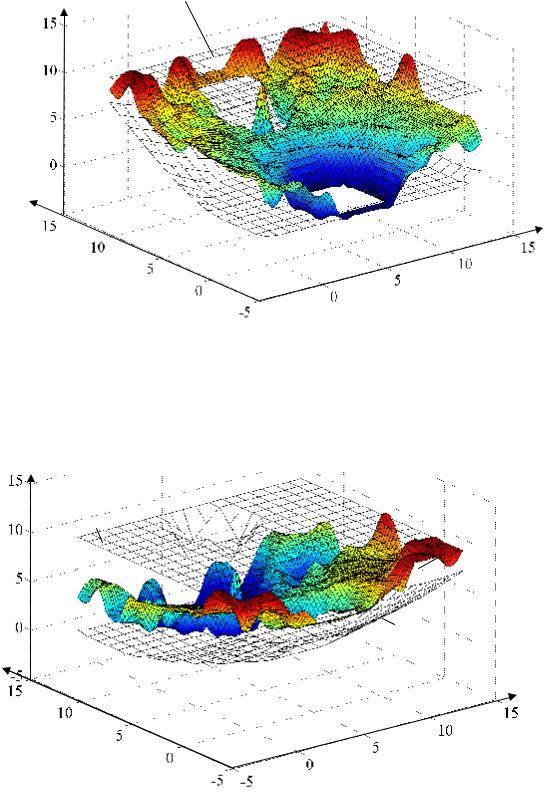
Рис. 4.48. Зависимость диапазонных qn9B, qn9Н и оптимального qn9 значений управляемой координаты q9 в начальной точке положения груза от положений базового шасси q1, q3 (серия экспериментов № 2)

qk9B, qk9Н, qk9, УЛЕ

qk9B

qk9

qk9Н

Рис. 4.49. Зависимость диапазонных qk9B, qk9Н и оптимального qk9 значений управляемой координаты q9 в конечной точке положения груза от положений базового шасси q1, q3 (серия экспериментов № 2)

265

qn10B, qn10Н, qn10, УЛЕ

qn10B

qn10

qn10Н

Рис. 4.50. Зависимость диапазонных qn10B, qn10Н и оптимального qn10 значений управляемой координаты q10 в начальной точке положения груза от положений базового шасси q1, q3 (серия экспериментов № 2)

qk10B, qk10Н, qk10, УЛЕ

qk10B

qk10

Рис. 4.51. Зависимость диапазонных qk10B, qk10Н и оптимального qk10 значений управляемой координаты q10 в конечной точке положения груза от положений базового шасси q1, q3 (серия экспериментов № 2)

266

Точки условного глобального минимума на рассматриваемой области, T=15,55 с

T, c

z1, УЛЕ

x1, УЛЕ

№ 1 № 2

Начало

z1, УЛЕ

Рис. 4.52. Зависимость временного критерия эффективности T от положений базового шасси q1, q3 при ограничении на предельную линейную скорость груза vлин пред= 0,4 УЛЕ/с (серия экспериментов № 2)

Y0, УЛЕ

X0, УЛЕ

Конец

Начало Конец

Z0, УЛЕ

Начало

Рис. 4.53. Пример траектории, оптимальной по временному критерию T при отсутствии препятствий в рабочей области, при положениях базового шасси q1=4; q3=14 УЛЕ

267

На рис. 4.44 и 4.45 в качестве примера приведены графики зависимостей временного критерия T от начального и конечного значений управляемых координат q8, q9, q10 при двух различных положениях базового шасси в пространстве: q1= –1; q3= –3 и q1= –3; q3= –3 УЛЕ. Значения глобальных минимумов на данных графиках несколько выше, чем на аналогичных зависимостях из первой серии экспериментов (см. рис. 4.35 и 4.36) вследствие действующих ограничений на скорость перемещения груза.

На рис. 4.46–4.51 приведены зависимости диапазонных ([qn8В;

qn8Н]; [qn9В; qn9Н]; [qn10В; qn10Н] [qk8В; qk8Н]; [qk9В; qk9Н]; [qk10В; qk10Н]) и оп-

тимальных (qn8, qn9, qn10, qk8, qk9, qk10) значений управляемых координат. На рис. 4.52 приведена зависимость временного критерия T.

Выводы по 2-й серии экспериментов аналогичны выводам по 1-й серии, за исключением того, что для графика временного критерия T, в отличие от 1-й серии экспериментов, симметрия наблюдается только относительно линии, соединяющей точки начального и конечного положений условного центра груза. Относительно вертикальной плоскости между начальным и конечным положениями груза, равноудаленной от них, симметрия не соблюдается. Вследствие этого две симметричные точки условного глобального минимума на рассматриваемой области находятся за конечным положением груза и ближе к последнему, чем к начальному положению груза (см. рис. 4.52).

Значение целевой функции (временного критерия, или времени реализации) для оптимальной траектории составляет T=15,55 с, что примерно в 3 раза больше времени реализации оптимальной траектории в серии экспериментов № 1, и не приводит к значительному раскачиванию и колебаниям груза.

Пример траектории, оптимальной по временному критерию T при отсутствии препятствий в рабочей области, при положениях базового шасси q1=4; q3=14 УЛЕ приведен на рис. 4.53.

Результаты 3-й серии экспериментов. В данной серии экспери-

ментов в качестве критерия эффективности также использовалось значение минимального времени перемещения T, учитывались ограничения по максимальным рациональным скоростям изменения управляемых координат ГПК вида (4.127), (4.133) и (4.138), в рабочей области присутствовали препятствия, задаваемые по (3.154) (тестовая схема).

Анализ результатов серии экспериментов № 3 позволяет сделать выводы о том, что наличие препятствий в рабочей области добавляет на графики зависимостей временного критерия T от начального и ко-

268

нечного значений управляемых координат q8, q9, q10 множество локальных экстремумов, что непредсказуемо меняет положение точки глобального минимума (рис. 4.54, 4.55) на указанных графиках и вследствие этого точки глобального минимума на графике зависимости целевой функции от положений базового шасси q1, q3.

T, с

Точка минимума № 1, T=35,6 с

qn10, qn9, qn8, рад

qk8, qk9, qk10, рад

Рис. 4.54. Зависимость временного критерия эффективности T от начального и конечного значений управляемых координат q8, q9, q10 при постоянных координатах базового шасси (УЛЕ) q1= –1; q3= –3 (серия экспериментов № 3)

T, с

Точка минимума № 2, T=38,8 с

qk8, qk9, qk10, рад

Рис. 4.55. Зависимость временного критерия эффективности T от начального и конечного значений управляемых координат q8, q9, q10 при постоянных координатах базового шасси (УЛЕ) q1= –3; q3= –3 (серия экспериментов № 3)

269