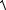2426

Вывод коэффициентов полинома четвертой степени для системы уравнений (4.15)–(4.18).

В уравнении тора (4.18), согласно выражению (4.16), в принятой системе координат x2+z2=ρ2. В то же время, согласно (4.30), ρ2 может быть выражено через y. Подставив (4.30) в (4.18), получим уравнение с одним неизвестным:

y4 ×(к2 +1)2 + y3 ×(2×(к2 +1)× 2×к × y0 )+

+ y2 ×(2×(h 2 + y 2 + R2 - r 2 ))+ y2 ×(2×к × y )2 +

+y ×(2× 2×к × y0 ×(h12 + y02 + R2 - r 2 ))+

+(h12 + y02 + R2 - r 2 )2 - 4× R2 × h12 - 4× R2 × y2 ×к2 -

- 4× R2 × y × 2× к × y0 - 4 × R2 × y02 = 0.1 0 0

Если обозначить

(к2 +1)2 = s1;

(2 × (к2 +1)× 2 × к × y0 )= s2 ;

2× (h12 + y02 + R2 - r2 )+ 22 × к2 × y02 - 4× R2 × к2 = s3;

4×к × y0 ×(h12 + y02 + R2 - r2 )- 4× R2 ×2×к × y0 = s4 ;

(h12 + y02 + R2 - r2 )2 - 4× R2 ×h12 - 4× R2 × y02 = s5 ,

то может быть получена классическая форма полинома четвертой степени:

Для каждого сочетания зна- Y1 2 чений q8 и q9 используется после-

довательность вычислений:

q8В=q8max;

q8Н=arctg(y4,43/(x3,33+q9min))+arccos((x1,2+ρ)/ 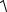y4,432 +(x3,33 + q9min )2 ); (4.85)

q9В=(x1,2+ρ–y4,43∙sin q8max)/cos q8max – x3,33;

q9Н=q9min.

При ρ2≤ρ<ρ3

q8В=arctg(y4,43/(x3,33+q9max))+arccos((x1,2+ρ)/ y4,432 + (x3,33 + q9max )2 );

В случае, если значение вылета ρ находится вне интервала конструктивно допустимых значений

203

делается вывод о невозможности обеспечить требуемые координаты груза при текущем положении базового шасси ГПК, алгоритм завершает свою работу.

2.3. По текущему значению ρ и граничным значениям координат [q8В q8Н]; [q9В q9Н] определяются граничные значения диапазона управляемой координаты [q10В q10Н].

ρ [ρ1;ρ4 ], используя (4.83), получим

2.4. В случае, если полученное по (4.91) значение q10В меньше минимальной конструктивно возможной длины грузовой лебедки от оголовка стрелы

делается вывод о невозможности обеспечить требуемые координаты груза, алгоритм завершает свою работу.

Если выполняется условие

где – знак логического умножения (конъюнкции), т.е. точка подвеса груза расположена внутри пространства возможных положений оголовка стрелы (позиция 4 на рис. 4.7), q10Н корректируется:

q10Н=q10min. (4.94)

После этого также последовательно корректируются значения q9Н и q8Н по (4.97) и (4.96) с подстановкой значения q10Н.

204

3. По значению одной из управляемых координат (q8, q9, q10), заданному внутри соответствующего диапазона [q8В q8Н], [q9В q9Н], [q10В q10Н], определяются значения двух оставшихся управляемых координат.

q8 определяется по (4.96).

Блок-схема алгоритма определения управляемых координат ГПК при нулевых углах наклона шасси приведена на рис. 4.20.

Рассмотренный алгоритм позволяет моделировать управляемые координаты ГПК для заданного положения груза, при нулевых углах наклона шасси; позволяет в автоматизированном режиме решать обратную задачу кинематики ГПК [103]. Алгоритм может использоваться при планировании траекторий перемещения груза, при решении задач кинематического анализа и синтеза конструктивных параметров ГПК и технологических параметров его рабочего процесса.

4.4.Методика проверки положения автомобильного крана

впространстве конфигураций по ограничению на устойчивость

Проверка положений ГПК на устойчивость является необходимым элементом обеспечения безопасной эксплуатации. Возможно выполнение данной проверки как для уже найденной, имеющейся траектории, так и в процессе поиска траектории, что позволяет заранее исключить неустойчивые конфигурации из рассмотрения. Методика проверки отдельного положения ГПК в пространстве конфигураций по ограничению на устойчивость, описанная в данном разделе,

206

использована как составляющая часть общей методики поиска оптимальной траектории в пространстве конфигураций ГПК.

Математическая модель динамической системы ГПК [104, 105], сведенная в систему из 11-ти дифференциальных уравнений второго порядка с постоянными коэффициентами с 11 неизвестными функциями – обобщенными координатами, позволяет решать задачи статики и динамики ГПК.

Статическая составляющая разработанной модели использовалась для оценки устойчивости ГПК и проверки положения ГПК в пространстве конфигураций по ограничению на устойчивость [86, 87, 93, 96, 111, 117, 119, 123, 127, 128].

Практическую значимость представляют при этом зависимости обобщенных координат qi, i [1;6], которые использовались для определения значений показателей устойчивости ГПК. Полученные обобщенные координаты также использовались для моделирования значений информационных

параметров для вычисления крите-

Рис. 4.21. Прямоугольный опорный рия устойчивости [93, 96]. контур ГПК

Для проверки устойчивости положения ГПК, имеющего прямоугольный опорный контур (рис. 4.21), в пространстве его конфигура-

ций предлагается использовать следующий критерий оценки устойчивости:

где k1, k2, 1/k1, 1/k2 – показатели устойчивости для четырех осей опрокидывания, входящих в опорный контур, вычисляемые на основе нормальных реакций в опорных элементах:

где R1, R2, R3, R4 – нормальные реакции на опорных элементах ГПК

(см. рис. 4.21).

Из этих показателей только два (k1, k2) являются независимыми. Аналитические выражения для вычисления критерия устойчиво-

сти (sgn – функция знака числа):

После подстановки (4.100) в (4.101) полное аналитическое выражение критерия будет иметь вид:

ξ=((1/k2)∙sgn(1+sgn(1/k1–1/k2))+(1/k1)∙sgn(1+sgn(1/k2– –1/k1)))∙sgn(1+sgn((k2∙sgn(1+sgn(k1–k2))+k1∙sgn(1+sgn(k2–k1)))–

– ((1/k2)∙sgn(1+sgn(1/k1–1/k2))+(1/k1)∙sgn(1+sgn(1/k2– –1/k1)))))+(k2∙sgn(1+sgn(k1–k2))+k1∙sgn(1+sgn(k2–

–k1)))∙sgn(1+sgn(((1/k2)∙sgn(1+sgn(1/k1–1/k2))+(1/k1)∙sgn(1+sgn(1/k2– –1/k1)))–(k2∙sgn(1+sgn(k1–k2))+k1∙sgn(1+sgn(k2–k1))))). (4.102)

Значение критерия устойчивости может быть также определено путем последовательных сравнений показателей устойчивости для четырех осей опрокидывания.

Для получения нормальных реакций R1, R2, R3, R4 на опорных элементах ГПК как первичных информационных параметров использовались отклонения обобщенных координат q2, q4, q5, q6, полученные в результате решения задачи статики при заданных больших значениях обобщенных координат q1…q11.

Вертикальное смещение δyio,0 характерной точки выносной гидравлической опоры io [1;4] ГПК вдоль оси O0Y0 инерциальной системы координат является второй компонентой вектора Rio,0 , задающе-

го смещения характерной точки опоры вдоль координатных осей инерциальной системы координат:

где Rio,1 – вектор положения характерной точки опоры io в локальной системе координат базового шасси, к которому относится масса каж-

да из локальной системы координат звена базового шасси в инерциальную с учетом как больших, так и малых значений обобщенных ко-

ординат (qj+qj), j=2;4;5;6.