Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2426

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

8.54 Mб

Скачать

☆

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 3919 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

é	–cosq6g×cosq5g	sinq5g	-sinq6g ×cosq5g	q1g	ù
é	–cosq6g×cosq5g	sinq5g	-sinq6g ×cosq5g	q1g	ù
ê					ú
ê	sinq6g×sinq4g -	cosq5g ×	cosq6g ×sinq4g +	q	ú
ê-cosq6g ×cosq4g ×sinq5g		×cosq4g	+sinq6g×cosq4g×sinq5g	2g ú
Tg= ê	sinq6g×cosq4g +	-cosq5g×	cosq6g ×cosq4g -	q	ú. (4.10)
ê	+cosq6g ×sinq4g ×sinq5g	×sinq4g	-sinq6g×sinq4g×sinq5g	3g	ú
ê	0	0	0	1	ú
ë	0	0	0	1	û

Координаты точки 1 в инерциальной системе координат обозначены как x1,0, y1,0, z1,0, а координаты точки 3 в инерциальной системе – как x3,0, y3,0, z3,0. Координаты точки 3 должны удовлетворять условиям:

x3,0=x1,0; y3,0=y1,0+q10, ; z3,0=z1,0,

(4.11)

где q10 – длина грузового каната, на которую, как и на все прочие управляемые координаты ГПК, конструктивно установлены извест-

ные предельные ограничения (q10min<q10<q10max).

Поскольку диапазон значений управляемой координаты q10 [q10В q10Н] изначально неизвестен, координаты точки 3 на данном этапе не могут быть найдены.

Используется точка 2 с координатами x2,0, y2,0, z2,0, расположенная также на грузовом канате, но выше точки 1 на любую известную (заданную) длину, например на 1 м. Тогда ее координаты в инерциальной системе могут быть определены как

x2,0=x1,0; y2,0=y1,0+1; z2,0=z1,0.

(4.12)

После того, как определены декартовы координаты точки 2 на грузовом канате и точки 1 подвеса груза, появляется возможность определения по ним диапазонов управляемых координат крана.

Базовое шасси крана в процессе работы должно оставаться неподвижным, поэтому первые 6 координат крана q1,…, q6 считаются постоянными. Их значения должны быть предварительно определены (измерены после установки выносных опор и фиксации базового шасси крана).

Задачу предлагается декомпозировать на несколько этапов. Вначале выражаются координаты точек 1 и 2, найденных в инерциальной системе координат, в локальной системе координат базового шасси крана O1X1Y1Z1. Для этого необходимо получить матрицу перехода от базового шасси крана к инерциальной системе координат T1 по формуле, аналогичной (4.9), с координатами q1… q6 в элементах матриц-

180

сомножителей, а затем обратить ее. Обратная матрица (T1)-1 будет выражать переход от инерциальной системы координат к системе координат базового шасси. Тогда вектор точки 1 в системе O1X1Y1Z1 определится как

R	= (T )−1	× R ,	(4.13)
1,1	1	1,0

где R1,0 – вектор положения точки 1 в инерциальной системе коорди-

нат вида [x1,0 y1,0 z1,0 1], компоненты которого найдены по формуле

(4.8).

Вектор точки 2 в системе O1X1Y1Z1 определится как

R	= (T )−1	× R ,	(4.14)
2,1	1	2,0

где R2,0 – вектор положения точки 2 в инерциальной системе коорди-

нат вида [x2,0 y2,0 z2,0 1], компоненты которого найдены по формуле

(4.12).

Полученные значения координат в системе базового шасси обо-

значены как (x1, y1, z1) для точки 1 и (x2, y2, z2) для точки 2. Используется известная форма записи уравнения прямой линии в

пространстве, проходящей через две точки с координатами x1, y1, z1 и x2, y2, z2:

x − x1			=	y − y1			=	z − z1			.	(4.15)

x	2	− x		y	2	− y		z	2	− z
		1				1				1

Для того чтобы определить диапазоны управляемых координат ГПК, необходимо найти точки пересечения этой прямой, совпадающей с направлением грузового каната и гравитационной вертикали, и границ некоторого пространства всевозможных значений первых трех управляемых координат крана q7, q8, q9. Сечение данного пространства любой плоскостью, проходящей через ось вращения поворотной колонки ГПК, показано на

Y1	2	Телескопическая
		Телескопическая
		стрела
		стрела
q8max		4

c1		1
c1	ρ	ρ
	ρ

Рис. 4.3. Область возможных положений оголовка стрелы ГПК

в координатах «вылет–высота» (ρ–Y1)

181

рис. 4.3. Это будет область возможных положений оголовка стрелы ГПК в координатах ρ–Y1. Здесь ρ – вылет стрелы. Его значение связано со значениями декартовых координат x и z оголовка стрелы в системе базового шасси зависимостью


ρ = x2 + z2 .			(4.16)

На рис. 4.3 прямые 1 и 2 – это образующие конических поверхностей, на которых угол подъема стрелы q8 принимает соответственно минимальное и максимальное значения, а дуги окружностей 3 и 4 – образующие торовых поверхностей, на которых величина выдвижения телескопического звена стрелы q9 соответственно минимальная и максимальная.

Y1 Конические поверхности

q10

Z1	q7
	Торовые

поверхности

Рис. 4.4. Пространство возможных положений оголовка стрелы

Рис. 4.5. Самопересекающийся тор – вид снаружи

То есть пространство возможных положений оголовка стрелы ГПК в системе координат O1X1Y1Z1 ограничено двумя коническими и двумя торовыми поверхностями, если ограничения по координате q7 отсутствуют, и дополнительно двумя плоскостями, если последние ограничения имеются (рис. 4.4).

Конструктивные ограничения для стреловых кранов имеются лишь по управляемым координатам

q8, q9 и q10, по координате q7 конструктивные ограничения отсутству-

ют.

Каждая из двух торовых поверхностей на рис. 4.4 – это внутренняя поверхность самопересекающегося тора (рис. 4.5, 4.6). Ось вращения тора будет совпадать с осью вращения поворотной части ГПК.

Чтобы определить диапазоны управляемых координат, необходимо найти две точки пересечения прямой линии грузового каната и граничных поверхностей простран-

182


ства возможных положений оголовка стрелы, если таковые сущест-
вуют. Каждая точка, расположенная как внутри пространства воз-
можных положений оголовка стрелы, так и на его границе,
однозначно определяет значения всех четырех управляемых
координат ГПК q7, q8, q9, q10.
Нижняя (по координате y) из найденных двух точек будет соот-
ветствовать минимальным значениям управляемых координат q8, q9,
q10, а верхняя – соответственно максимальным. Данные две точки на-
званы образующими интервал.
Возможен вариант, когда точка								Y2
подвеса		груза		сама	расположена

внутри		пространства			возможных
положений оголовка стрелы. Тогда									q8
нижняя из двух образующих интер-
вал точек положения оголовка будет									X1, X2
находиться не на границе простран-
									q7
ства, а внутри него, а именно выше
точки подвеса груза на минимально
возможную длину грузового каната.
То есть возможны три основных							Рис. 4.6. Внутренняя поверхность
варианта расположения образующих
интервал точек положения оголовка							самопересекающегося тора
стрелы (рис. 4.7): 1 – верхняя точка
на конической поверхности, нижняя на торовой поверхности; 2 –
верхняя и нижняя точки на торовых поверхностях; 3 – верхняя точка
на торовой поверхности, нижняя на конической поверхности.
И, наконец, при любом из пере-							Y1	2	3
численных трех вариантов возможно
смещение нижней образующей ин-							1		4

тервал точки внутрь пространства,
если точка подвеса груза располо-
жена внутри пространства возмож-
ных	положений			оголовка		стрелы
(например, позиция 4 на рис. 4.7).
Таким			образом,		необходимо				ρ
найти	декартовы координаты двух

образующих интервал точек в сис-							Рис. 4.7. Варианты расположения
теме координат базового шасси, а по							образующих интервал точек
ним – диапазоны значений управ-								оголовка стрелы
ляемых координат ГПК q7, q8, q9, q10.

183

Решение первой из указанных задач возможно в трехмерном евклидовом пространстве путем нахождения точек пересечения прямой, описываемой уравнением (4.15), и конической либо торовой поверхности.

Коническая поверхность описывается уравнением второго порядка

x2	+	z2	+	y2	= 0 ,	(4.17)
a2		b2		c2

где a, b, c – некоторые постоянные.

Тор описывается уравнением четвертого порядка

(x2 + z2 + y2 + R2 - r2 )2 - 4× R2 ×(x2 + z2 )= 0,

(4.18)

где R – расстояние от центра окружности до оси вращения; r – радиус окружности.

Система уравнений (4.15), (4.17) для случая пересечения прямой с конусом может быть сведена к квадратному уравнению второго порядка с одним неизвестным и довольно просто решена, однако аналитическое решение системы уравнений (4.15), (4.18) для случая пересечения прямой с тором хотя и возможно путем сведения к полиному четвертой степени с одним неизвестным и нахождению его корней, но слишком сложно и громоздко для практического применения. Приведение формул решения занимает при этом несколько десятков страниц.

Гораздо проще и быстрее найти корни полинома четвертой степени численным методом с использованием средств вычислительной техники и специальных программных продуктов, реализующих известные итерационные методы: секущих, сопровождающей матрицы,

Лагерра и др. [65, 147, 191, 193].

Вывод коэффициентов полинома четвертой степени для системы уравнений (4.15)– (4.18) пересечения прямой с тором в трехмерном пространстве приведен ниже.

Задача нахождения координат образующих интервал точек в системе базового шасси может быть сравнительно просто решена аналитически, путем сведения пространственной задачи к плоской.

При переходе от трехмерной декартовой системы координат базового шасси к цилиндрической формулы перехода будут иметь вид


ρ = x2 + z2 ; q7=arctg(z/x); y=y.			(4.19)
184

Здесь координата q7 будет соответствовать углу поворота поворотной колонки, а координата ρ – вылету стрелы.

Если затем временно исключить из рассмотрения координату поворота q7, то получается плоская задача в декартовой системе координат «вылет–высота» (ρ–Y1). В данной системе координат коническая поверхность всегда проецируется в прямую линию, а торовая поверхность – в дугу окружности.

Определенная сложность воз-							Y1
никает в том, что прямая линия							Y1
никает в том, что прямая линия
грузового каната, совпадающая с
гравитационной вертикалью, при
переводе в плоскую систему коор-
динат (ρ–Y1) получает вид кривой
второго порядка с небольшой кри-
визной, если углы наклона базово-
го шасси относительно гравитаци-										ρ
онной вертикали имеют ненуле-										ρ
онной вертикали имеют ненуле-							Рис. 4.8. Примерный вид линий
вые значения (рис. 4.8).							Рис. 4.8. Примерный вид линий
Чтобы		получить				наиболее	грузового каната в системе координат
простой вид			уравнения			прямой	(ρ–Y1) при ненулевых углах наклона
грузового каната в системе коор-							шасси
грузового каната в системе коор-
динат (ρ–Y1), используется схема,
приведенная на рис. 4.9.
Уравнение прямой						(4.15) в
плоскости x1–z1 имеет вид							ρ	1	2	l1,2
							Y1	1		l1,2
	x − x1		=	z − z1	.	(4.20)	Y1			Z1
	x − x1			z − z1			h1

	x2 − x1			z2 − z1					h2
	x2 − x1			z2 − z1			3		h2
							3
Уравнение данной прямой на
плоскости можно также записать в							X1
виде							X1
	A·x+B·z+C=0,					(4.21)	Рис. 4.9. Схема для определения
где							уравнения линии грузового каната
A=1/(x2–x1); B=–1/(z2–z1);							(вид сверху на поворотную колонку)
A=1/(x2–x1); B=–1/(z2–z1);

C=z1/(z2–z1) – x1/(x2–x1). (4.22)

Расстояние от данной прямой до точки с нулевыми координатами (начало системы координат на рис. 4.9) определится как

185

h1	=		C		.	(4.23)


		A2		+ B2
		A2		+ B2

Зная координаты x1, z1 точки 1, можно определить ρ по формуле (4.16). В то же время по схеме (см. рис. 4.9) ρ2=h12+h22. Тогда


h =	ρ 2 - h 2 .	(4.24)
2	1

По данной формуле может быть найдено численное значение h2 для точки 1.

Поскольку h2 – расстояние между проекциями двух точек 1 и 3, лежащими на прямой линии в пространстве, можно представить h2 как функцию от вертикальной координаты y:

h2=y·к+y0,

(4.25)

где к и y0 – некоторые постоянные.

Поскольку координаты точек 1 и 2 в системе координат базового шасси находятся по формулам (4.13), (4.14), коэффициент пропор-

циональности к может быть определен как
к=l1,2/∆y1,2,	(4.26)

где l1,2 = 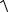(Dx1,2 )2 + (Dz1,2 )2 ; ∆x1,2=│x1–x2│; ∆z1,2=│z1–z2│; ∆y1,2=│y1–

–y2│.

Подставив в уравнение (4.24) значение y1 как компоненты вектора R1,1 точки 1, определенного по (4.12), можно определить y0 как

y0=h2 –y1·к.

(4.27)

Формула (4.24) справедлива для любой точки на прямой гравитационной вертикали (для любых значений ρ и h2), поэтому может быть получена зависимость вертикальной координаты y от вылета ρ для конкретного расположения прямой в системе O1X1Y1Z1:


y × к + y		0	=	ρ 2 - h 2 ,					(4.28)
		0					1
отсюда
y = (							)
y = (	ρ	2 − h		2	− y	0	)	к .	(4.29)
			1			0
			186

Или обратная зависимость:

ρ 2 = h 2

+ (y × к + y

)2 .

(4.30)

Границы области возможных положений оголовка стрелы в ко-

ординатах «вылет–высота» (ρ–y) будут заданы следующими уравне-

ниями (см. рис. 4.3):

линия 1:

y=к1·ρ+y01;

(4.31)

линия 2:

y=к2·ρ+y02;

(4.32)

линия 3:

(ρ–c1)2+y2=(R3)2;

(4.33)

линия 4:

(ρ–c1)2+y2=(R4)2,

(4.34)

где к1, к2, y01, y02, R3, R4, – конструктивно заданные постоянные.

Для их определения воспользу-

емся схемой на рис. 4.10. Согласно

этой схеме, по теореме синусов,

y01

yc1

yc2

; yc1 =

;

yc1

sin(90° - q8 )

sin 90°

yc2 ;

cosq8

zc1

sin(90° - q8 )

sin q8

yc2 = c1 × tg(q8 );

yc2=yc1+y01;

(90°–q8)

y01 = c1

× tg(q8min )-

;

(4.35)

cos(q8min )

Рис. 4.10. Схема для определения

y02 = c1

× tg(q8max )-

. (4.36)

постоянных к1, к2, y01, y02, R3, R4

cos(q8max )

к1=tg(q8min);

(4.37)

к2=tg(q8max);

(4.38)

R3 =

(c2 + q9min )2 + (c3 )2 ;

(4.39)

R4 =

(c2 + q9max )2 + (c3 )2 .

(4.40)

После определения коэффициентов уравнений (4.31)–(4.34) необ-

ходимо решить четыре системы уравнений: (4.30)–(4.31), (4.30)–

(4.32), (4.30)–(4.33) и (4.30)–(4.34).

Решения систем уравнений (4.30)–(4.31) и (4.30)–(4.32) имеют

вид соответственно

187

к × y

× к + к2 × к × y

- к × к

× h

+ h

к1 ×ç

± + 2 × к × y0 × y01 +

× y01

y =

+ y0

ø + y01 ;

(к2 × к

-1)

(4.41)

к × y

× к

+ к2 × к

× y

±ö

- к × к

2 × h 2

+ h

2 + ÷

- к2 ×ç

± + 2 × к × y0 × y02 +

+ y0

+ к

× y02

y =

ø + y02 .

(4.42)

(к2 × к2

2 -1)

Причем используются только положительные значения y, кото-

рым, как показали расчеты, соответствует знак «+» перед квадратным

корнем.

Системы уравнений (4.30)–(4.33) и (4.30)–(4.34) могут быть све-

дены к уравнению с одним неизвестным четвертой степени, которое,

как отмечалось, гораздо легче решить численно, чем аналитически.

Однако можно обойтись и без численных методов, если провести

линеаризацию кривой грузового каната в координатах (ρ–Y1), описы-

ваемой уравнением (4.30), в окрестностях ее пересечения с заданной

дугой 4 (или 3) окружности (рис. 4.11).

ρ0=const

Линеаризация

для

пересечения

yв

линии грузового каната с дугой 4

включает

предварительное

определе-

yд4

ние вертикальной координаты y4 (см.

yн

рис. 4.11) пересечения вертикальной

прямой линии вылета ρ0=const точки 1

подвеса груза с координатами x1, z1

Точка 1

ρ0 =

x12 + z12 ,

(4.43)

ρ0

ρн

ρв

Рис. 4.11. Схема линеаризации

дуги

описываемой

уравнением

уравнения грузового каната

(4.34)

для пересечения с дугой 4

2 - (ρ0 - c1 )2 . (4.44)

y4 =

188

Действительное значение yд4 вертикальной координаты точки пе-
ресечения линии грузового каната и дуги 4 будет отличаться от y4, ес-
ли имеются ненулевые углы наклона базового шасси относительно
гравитационной вертикали.
Необходимо определить значения вылета ρ двух точек на линии
грузового каната с вертикальными координатами, большими и
меньшими y4 на некоторую постоянную величину cy (см. рис. 4.11).
Значение cy будет определяться конструкцией ГПК (типоразмером)
и должно быть подобрано таким образом, чтобы для любых коор-
динат точки груза при любых допустимых углах наклона базового
шасси точка пересечения yд4 линии грузового каната и дуги окруж-
ности 4 оказалась внутри интервала [(y4+cy)						(y4–cy)].
Это означает, что cy должно
быть	больше		определенного				cy	q8
минимально допустимого				зна-	Касательная		yc	h
чения.
Для приближенного вычис-
ления	минимально возможного
значения cy используется схема,					q8			αc
изображенная на рис. 4.12.
Согласно			этой	схеме	R4	y0z
tg(q8)=h/cy;			αc=h/yc;

yc=sin(q8 )× R4 + y0z , отсюда					Рис. 4.12. Схема для приближенного
	α
		)×(sin(q8)	×R4 + y0z ), (4.45)		определения минимального
cy = tg(qc						значения cy
	8
где αc – максимальный суммарный угол наклона базового шасси от-
носительно гравитационной вертикали.
Так, например, если принять αc=3°=0,05236 рад, то для конструк-
ции ГПК с R4=20 м и y0y=3 м при варьировании q8 от 10 до 80° мини-
мально допустимое значение cy будет равно 1,92 м. В данном случае
целесообразно принять cy=2 м.
При обозначении

yв=y4+cy; yн=y4–cy.

(4.46)

Согласно (4.30) ρ определится как

ρ =		.
	h12 + (y × к + y0 )2		(4.47)
189

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 3919 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20218.25 Mб472420.pdf
#
07.01.20218.32 Mб142421.pdf
#
07.01.20218.36 Mб42422.pdf
#
07.01.20218.38 Mб82423.pdf
#
07.01.20218.44 Mб62425.pdf
#
07.01.20218.54 Mб72426.pdf
#
07.01.20218.55 Mб82427.pdf
#
07.01.20218.59 Mб52428.pdf
#
07.01.2021367.33 Кб5243.pdf
#
07.01.20218.61 Mб912430.pdf
#
07.01.20218.7 Mб332431.pdf